-
分割学习(loss and Evaluation)
参考
语义分割的损失函数
(交叉熵损失函数)
- 逐像素的交叉熵
- 还需要考虑样本均衡问题(有的)
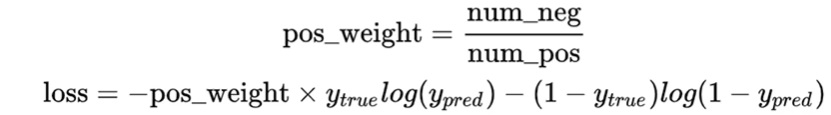
这里的交叉熵损失函数增加了pos_weight参数。前景和背景的比例不一样,使每一个像素点的重要程度不一致。一般情况我们按照正例和负例的比例设置该参数。
这里再解释下二分类交叉熵损失函数(去掉pos_weight):
损失函数越小越好- log函数如下
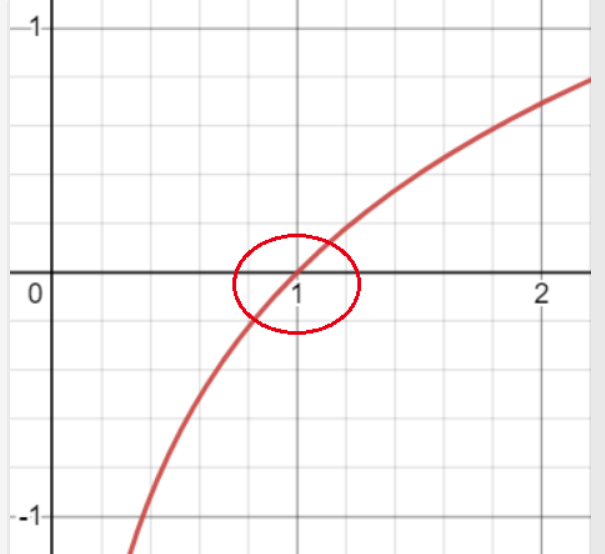
由图像可以看出当X值越接近于1的时候Y的绝对值越小,当X值越接近0时Y的绝对值越大。
eg:
y_true:真实样本标签0, 1
y_pred:样本预测标签0,1- y_true=0 y_true=1 y_pred=0 此时带入loss函数,loss=0, 可以看到当y_true=0的时候,y_pred越接近于0,loss函数的绝对值越小 当y_true=1的时候,y_pred越接近于0,loss函数的绝对值越大 y_pred=1 当y_true=0的时候,y_pred越接近于1,loss函数的绝对值越大 当y_true=1的时候,y_pred越接近于1,loss函数的绝对值越小 由此可以看到, y_pred越接近真实标签y_true,其损失函数越小, 月能够区分前景标签1和背景标签0。
我们还需要注意y_true log(y_pred)时判断真实标签为1与预测标签的损失,想想,当真实标签为0的时候,该部分直接就是0, 所以另一部分时判断真实标签为0的损失(Focal loss)
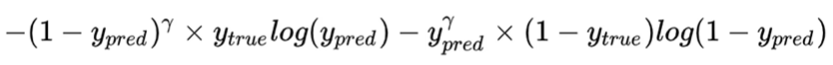
思路:像素点难易之分:越难分的样本,对其奖励越大。
实现:基于交叉熵损失函数, 增加真实标签0和1与预测标签0和1差值的 γ \gamma γ乘方参数。假设 γ \gamma γ=2
二次平方函数的图像如下:
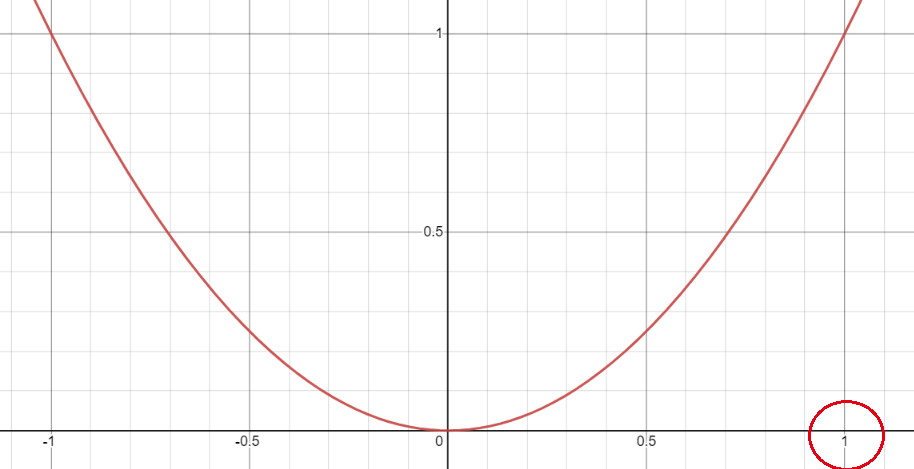
我们可以看到,该函数的在区间[0, 1]之间的增长趋势是递增的, 所以当当真实标签y_true和预测标签y_pred相差很大的时候,差值接近于1,其平方项后的值也就很大, 差值接近与1的时候, 其平方项后的值也就很小, 所以对与容易分割的样本,对其损失激励很小, 对难分的样本,其损失激励就很大了。这样对难易样本(或像素)有所区分。在结合样本数量的权值 α \alpha α(上述说的正负样本的比例pos_weight)后,就是完整的Focal Loss函数了。
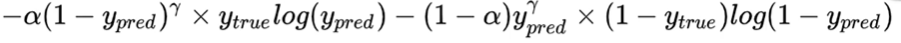
评估标准
IoU:交并比(图中黄色部分的交集/黄色部分并集)

MIoU(计算所有类别的平均值, 一般当作分割任务评估指标)
-
相关阅读:
基于java+springmvc+mybatis+vue+mysql的校园安全管理系统
《Netty实战》读书笔记
申请知识产权需要什么条件?
Vite+React+Electron开发入门,10分钟搭建本地环境并打包
Linux C/C++ 多线程开发 - 基础介绍
OOP 多重收纳(类模板)
从c到c++
文心一言 VS 讯飞星火 VS chatgpt (97)-- 算法导论9.3 3题
进程控制——进程创建
开发工程师必备————【Day16】数据库知识补充
- 原文地址:https://blog.csdn.net/qq_40837795/article/details/126242591