• 数据结构与算法笔记七（暴力递归到动态规划）

    暴力递归到动态规划

    阶段：

    尝试，递归 --》 记忆化搜索，DP --》 严格表结构，DP --》 严格表精版

    某些问题上，记忆化搜索 和 严格表结构 用同样的时间复杂度。

    机器人运动问题

    一个整数n代表 你有n个位置，
    一个整数s代表 开始的位置， 1到n之间。
    一个整数e 代表 代表要去的 目标位置
    一个整数k 代表 机器人必须走k步

    走的规则： 1位置只能走向2， n位置下一步只能走向n-1

    问： 走k步，从s到e有多少种方法？

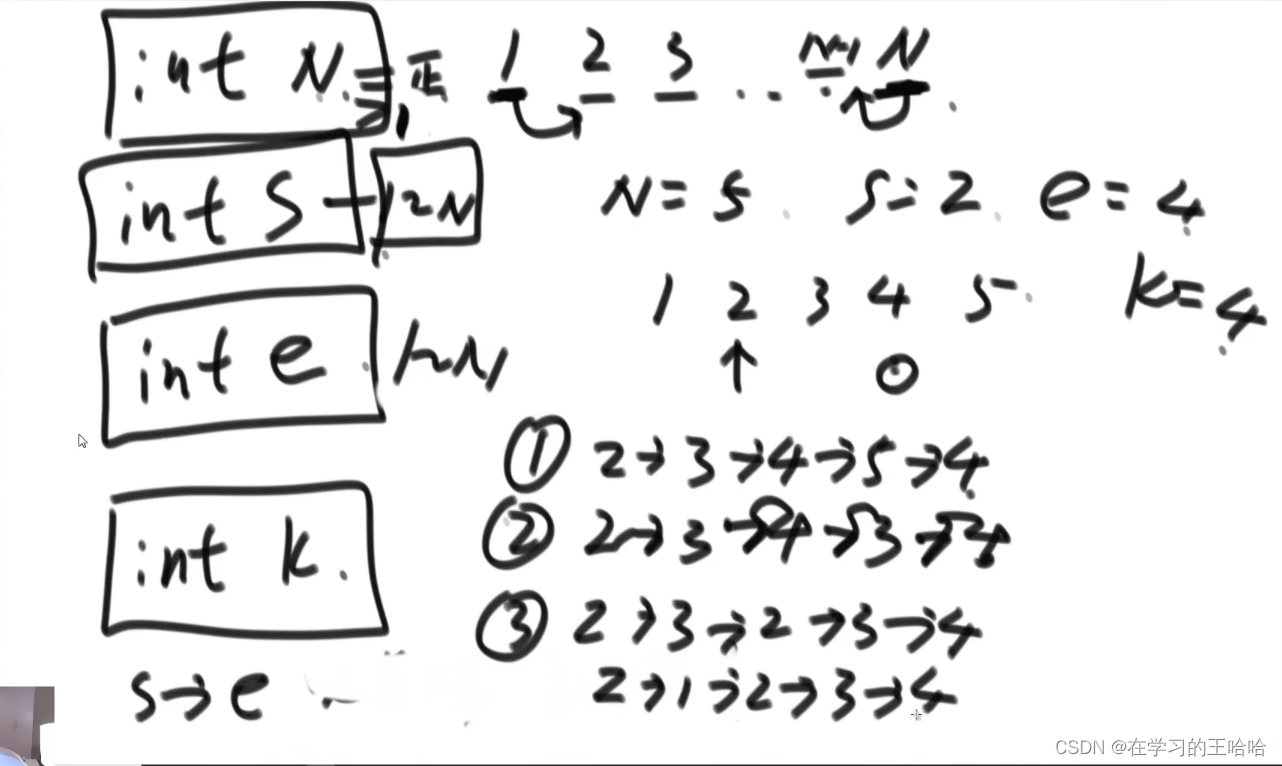    在这里插入图片描述展开表示：
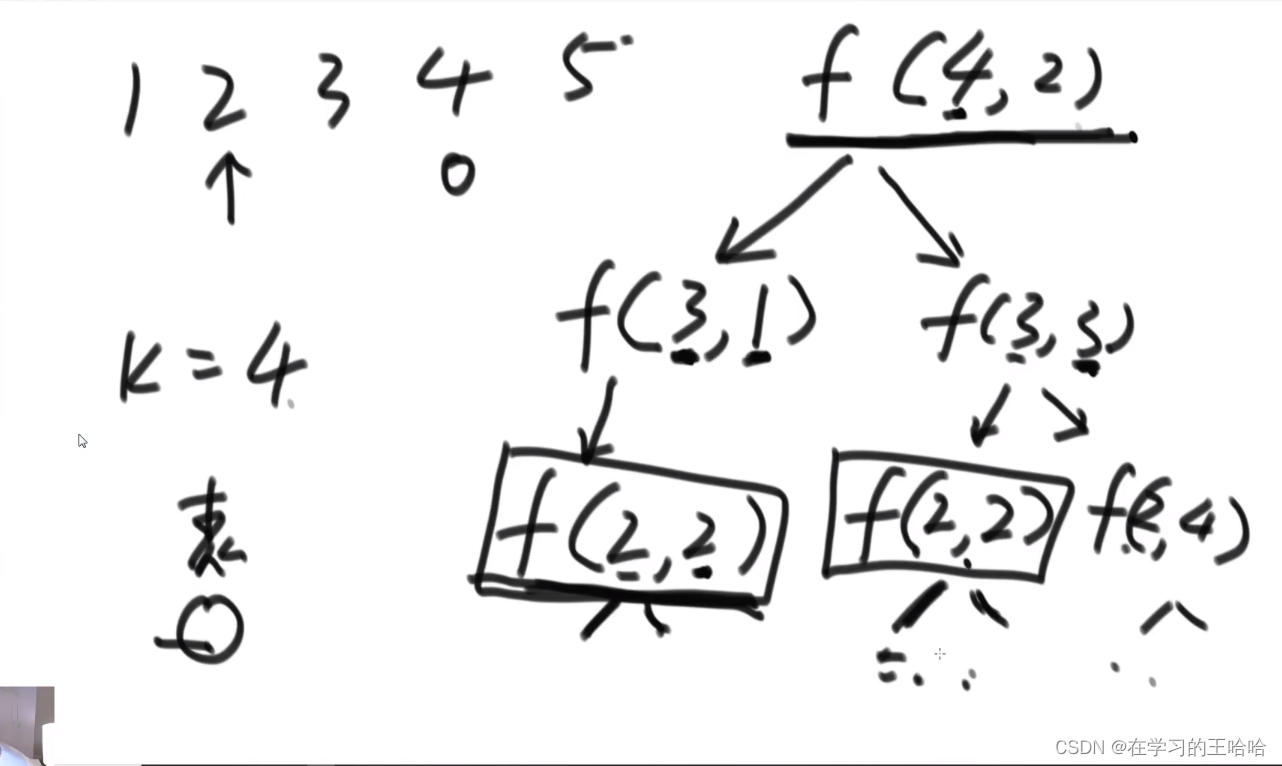
    在这里插入图片描述
    暴力递归：

    public static int ways1(int N, int M, int K, int P) {
		// 参数无效直接返回0
		if (N < 2 || K < 1 || M < 1 || M > N || P < 1 || P > N) {
			return 0;
		}
		// 总共N个位置，从M点出发，还剩K步，返回最终能达到P的方法数
		return walk(N, M, K, P);
	}

	// N : 位置为1 ~ N，固定参数
	// cur : 当前在cur位置，可变参数
	// rest : 还剩res步没有走，可变参数
	// P : 最终目标位置是P，固定参数
	// 该函数的含义：只能在1~N这些位置上移动，当前在cur位置，走完rest步之后，停在P位置的方法数作为返回值返回
	public static int walk(int N, int cur, int rest, int P) {
		// 如果没有剩余步数了，当前的cur位置就是最后的位置
		// 如果最后的位置停在P上，那么之前做的移动是有效的
		// 如果最后的位置没在P上，那么之前做的移动是无效的
		if (rest == 0) {
			return cur == P ? 1 : 0;
		}
		// 如果还有rest步要走，而当前的cur位置在1位置上，那么当前这步只能从1走向2
		// 后续的过程就是，来到2位置上，还剩rest-1步要走
		if (cur == 1) {
			return walk(N, 2, rest - 1, P);
		}
		// 如果还有rest步要走，而当前的cur位置在N位置上，那么当前这步只能从N走向N-1
		// 后续的过程就是，来到N-1位置上，还剩rest-1步要走
		if (cur == N) {
			return walk(N, N - 1, rest - 1, P);
		}
		// 如果还有rest步要走，而当前的cur位置在中间位置上，那么当前这步可以走向左，也可以走向右
		// 走向左之后，后续的过程就是，来到cur-1位置上，还剩rest-1步要走
		// 走向右之后，后续的过程就是，来到cur+1位置上，还剩rest-1步要走
		// 走向左、走向右是截然不同的方法，所以总方法数要都算上
		return walk(N, cur + 1, rest - 1, P) + walk(N, cur - 1, rest - 1, P);
	}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37

    第一步优化： 记忆化搜索，就加了缓存

    第二步优化： 动态规划，纠结位置依赖顺序
    严格表结构的动态规划。
    时间复杂度：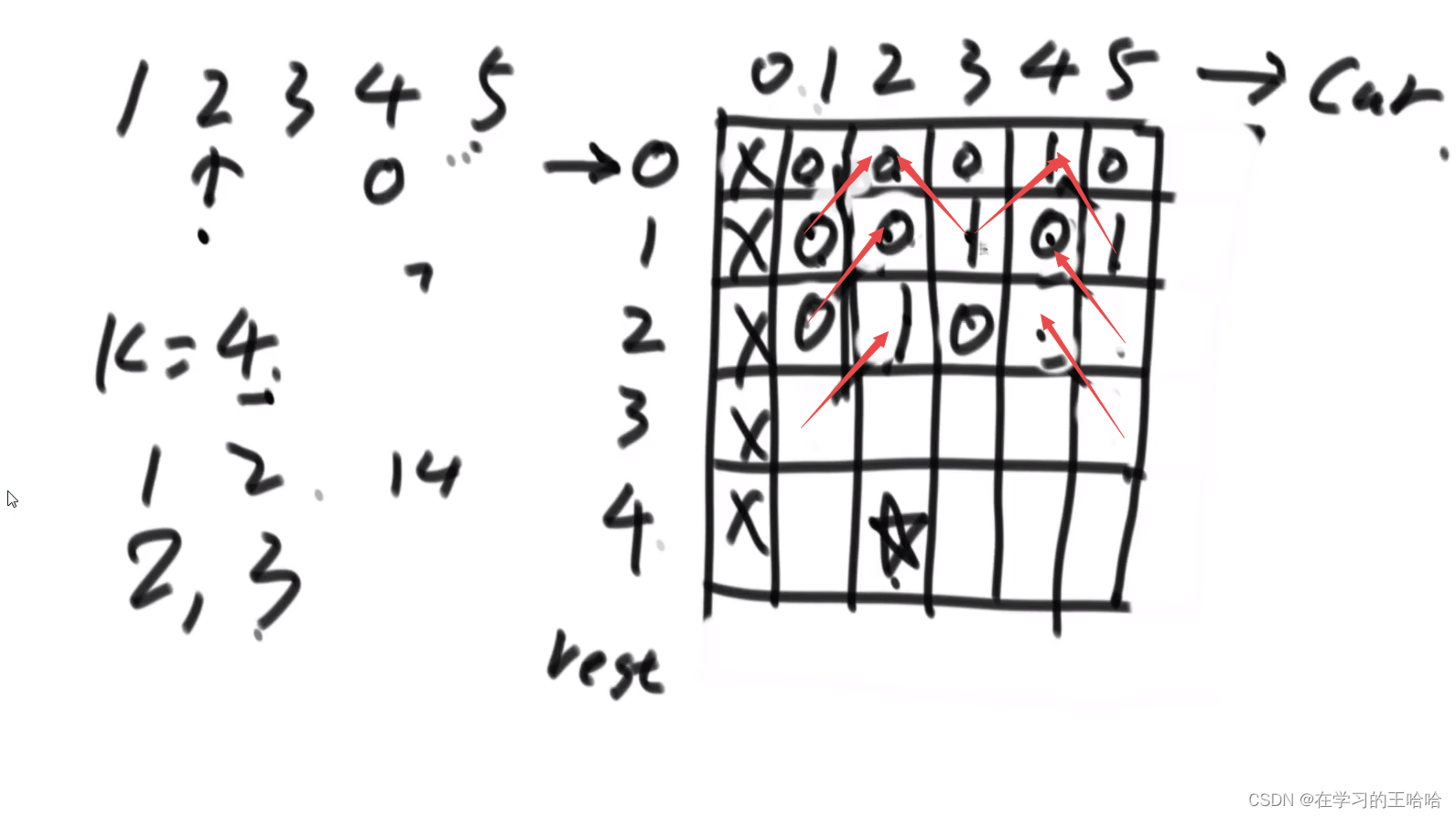

    在这里插入图片描述

    硬币问题

    leetcode322
    给你一个正数数组，里面每一个值，代表一枚硬币的面值。
    一个数代表一枚硬币。

    aim = 10.
    组成这个10，最少用多少硬币。 7 + 3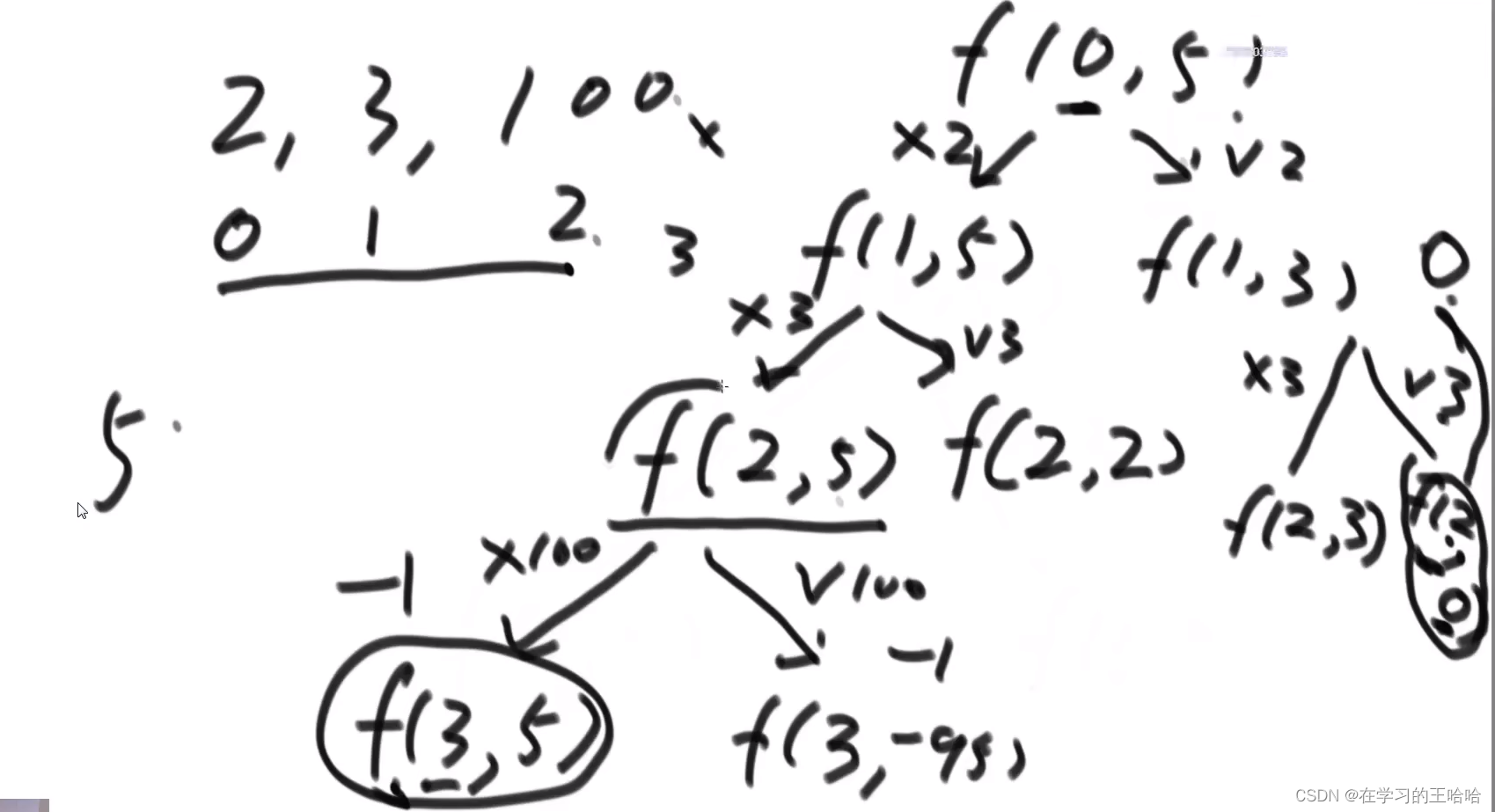

    在这里插入图片描述

    递归：

    package com.wanghaha.algorithm;

public class Day8_03_62CoinsMin {

    public static int minCoins1(int[] arr, int aim){
        process(arr, 0, aim);
    }

    // arr[index..]组成出rest这么多钱，最少的硬币数量返回
    public static int process(int[] arr, int index, int rest){
        if(rest < 0){
            return -1;
        }
        if( rest == 0 ){
            return 0;
        }
        // rest > 0
        if(index == arr.length ){
            return -1;
        }
        // rest > 0 and  也有硬币
        int p1 = process(arr, index +1 , rest);
        int p2Next = process(arr, index + 1 , rest - arr[index]);
        if(p1 == -1 && p2Next == -1){
            return -1;
        }else {
            if(p1 == -1){
                return p2Next + 1 ;
            }
            if(p2Next == -1 ){
                return p1;
            }
        }
        return Math.min(p1, p2Next);
    }
}


    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37

    记忆化搜索

        public static int minCoins2(int[] arr, int aim){
        int[][] dp = new int[arr.length  +1 ][aim + 1];

        for (int i = 0; i < arr.length + 1; i++) {
            for (int j = 0; j < aim + 1; j++) {
                dp[i][j] = -2;
            }
        }
        return process2(arr, 0, aim, dp);
    }

    // arr[index..]组成出rest这么多钱，最少的硬币数量返回
    public static int process2(int[] arr, int index, int rest,int[][] dp){
        if(rest < 0){
            return -1;
        }
        if(dp [index][rest] != -2 ){
            return dp[index][rest];
        }

        if( rest == 0 ){
            dp[index][rest] = 0;
        }else if (index == arr.length ){
            dp[index][rest] = -1;
        }else {
            int p1 = process2(arr, index +1 , rest,dp);
            int p2Next = process2(arr, index + 1 , rest - arr[index],dp);
            if(p1 == -1 && p2Next == -1){
                dp[index][rest] =  -1;
            }else {
                if(p1 == -1){
                    dp[index][rest] = p2Next + 1 ;
                }else if (p2Next == -1 ){
                    dp[index][rest] = p1;
                }else {
                    dp[index][rest] = Math.min(p1, p2Next);
                }
            }
        }

        return dp[index][rest];
    }

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42

    严格表结构

        public static int minCoins3(int[] arr, int aim){
        int N = arr.length ;
        int[][] dp  = new int[N + 1][aim + 1];
        for (int row = 0; row < N ; row++) {
            dp[row][0] = 0;
        }
        for (int col = 1; col < aim; col++) {
            dp[N][col] = -1;
        }
        for (int index = N-1; index >= 0 ; index--) {
            for (int rest = 1; rest <= aim; rest++) {
                int p1 = dp[index+1][rest];
                int p2Next = -1;
                if(rest - arr[index] >= 0 ){
                    p2Next = dp[index+1][rest - arr[index]];
                }

                if(p1 == -1 && p2Next == -1){
                    dp[index][rest] =  -1;
                }else {
                    if(p1 == -1){
                        dp[index][rest] =   p2Next + 1 ;
                    }else if (p2Next == -1 ){
                        dp[index][rest] =   p1;
                    }else {
                        dp[index][rest] =   Math.min(p1, p2Next+1);
                    }
                }
            }
            
        }
        return dp[0][aim];
    }

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33

    递归：
    记忆化搜索
    严格表结构：

    1. 分析可变参数的变化范围
    2. 标出你要计算出来的终止位置
    3. 根据basecase，标出不用计算直接出答案的 位置
    4. 推普遍的位置如何依赖其他位置的。
    5. 定出严格表从哪些格子推到哪些格子，然后到终止位置。确定依次计算的顺序。 递归代码拿过来改

    拿数字

    有两个人玩游戏，能看到一个数组上所有的数字。
    每个人依次拿，只能拿最左或者最右的数组。
    两个人都很聪明，谁最后会获胜？返回获胜的分数。

    先手和后手

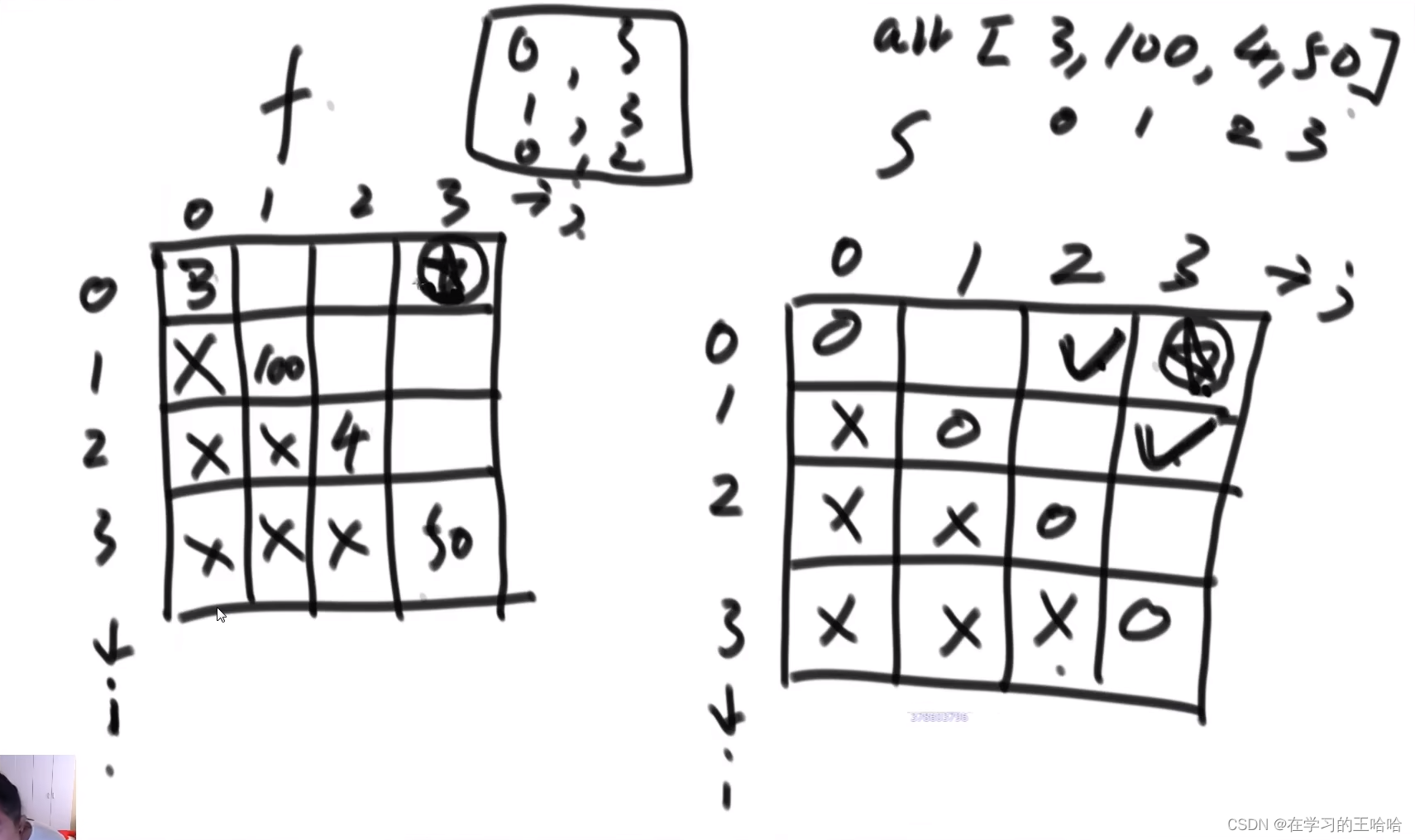
    在这里插入图片描述

    package com.wanghaha.algorithm;

import java.util.List;

public class Day8_04_65GrapNumber {

    public static int grapNumber(int[] arr){
        if(arr == null || arr.length ==0 ){
            return 0;
        }
        return Math.max(f(arr, 0, arr.length-1), s(arr, 0, arr.length-1));
    }

    public static int f(int[] arr, int i, int j ){
        if(i == j){
            return arr[i];
        }
        return Math.max(arr[i] + s(arr, i+1, j), arr[j] + s(arr, i, j-1) );
    }

    private static int s(int[] arr, int i, int j) {
        if(i == j){
            return 0;
        }
        return Math.min(f(arr, i+1, j), f(arr, i, j-1));
    }

    public static int grapNumber2(int[] arr){
        if(arr == null || arr.length ==0 ){
            return 0;
        }
        int[][] firstDP = new int[arr.length][arr.length];
        int[][] secondDP = new int[arr.length][arr.length];
        for (int i = 0; i < arr.length; i++) {
            firstDP[i][i] = arr[i];
            secondDP[i][i] = 0;
        }
        int j = 1;
        int i = 0;
        int a;
        int b;
        while (j != arr.length){
            System.out.println("j: " + j);
            a = i;
            b = j;
            while (a<arr.length && b< arr.length){
                firstDP[a][b] = Math.max(arr[a] + secondDP[a+1][b], arr[b] + secondDP[a][b-1]);
                secondDP[a][b] = Math.min(firstDP[a+1][b],firstDP[a][b-1]);
                a ++ ;
                b ++ ;
            }
            j++;
        }
        return Math.max(firstDP[0][arr.length-1],secondDP[0][arr.length-1]);

    }




    public static void main(String[] args) {
        int[] arr = {1,9,11};
        System.out.println(grapNumber(arr));
        System.out.println(grapNumber2(arr));
    }
}


    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67

    象棋

    马 ，10乘9的棋盘上，从 （0，0） 要到 （a,b）去
    一定要跳K步
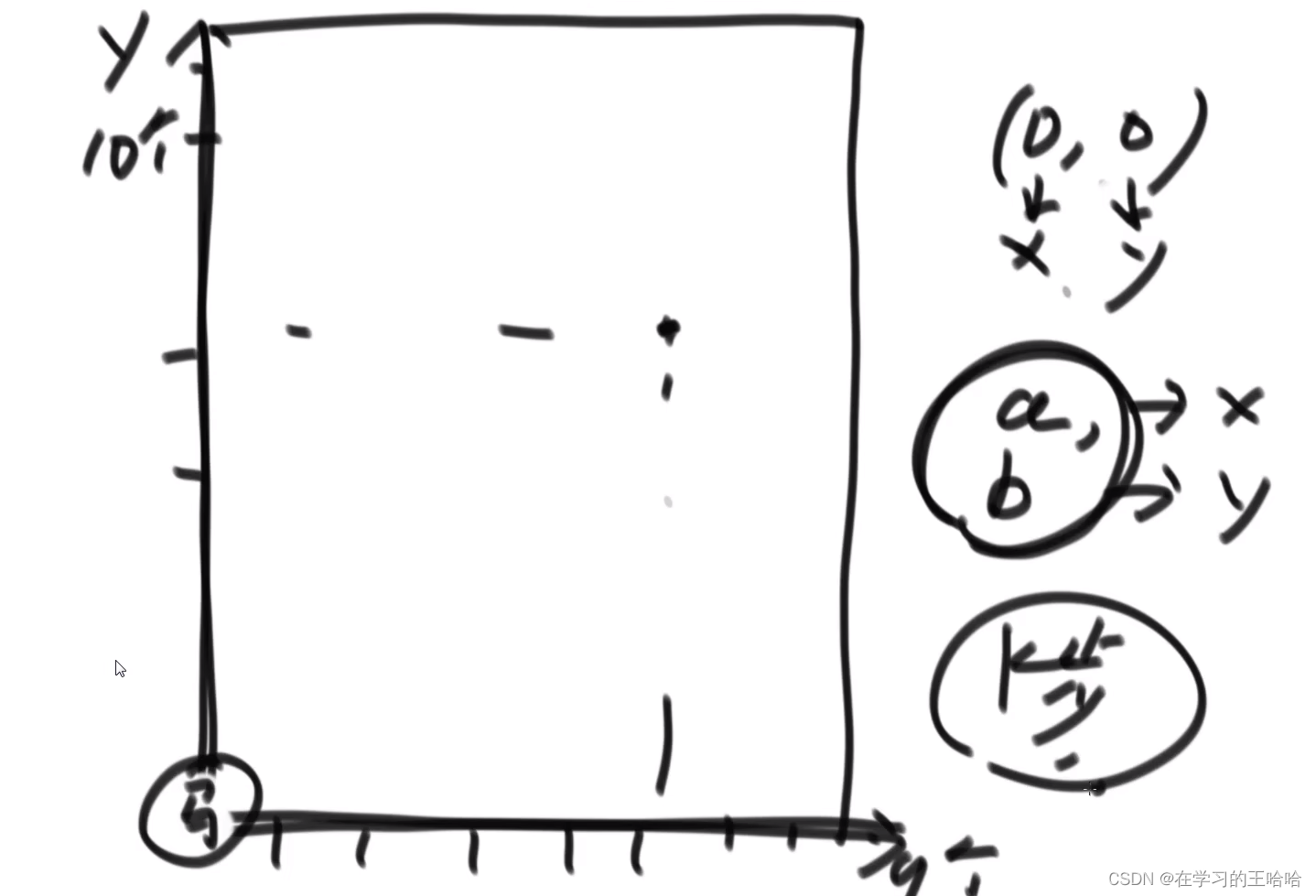
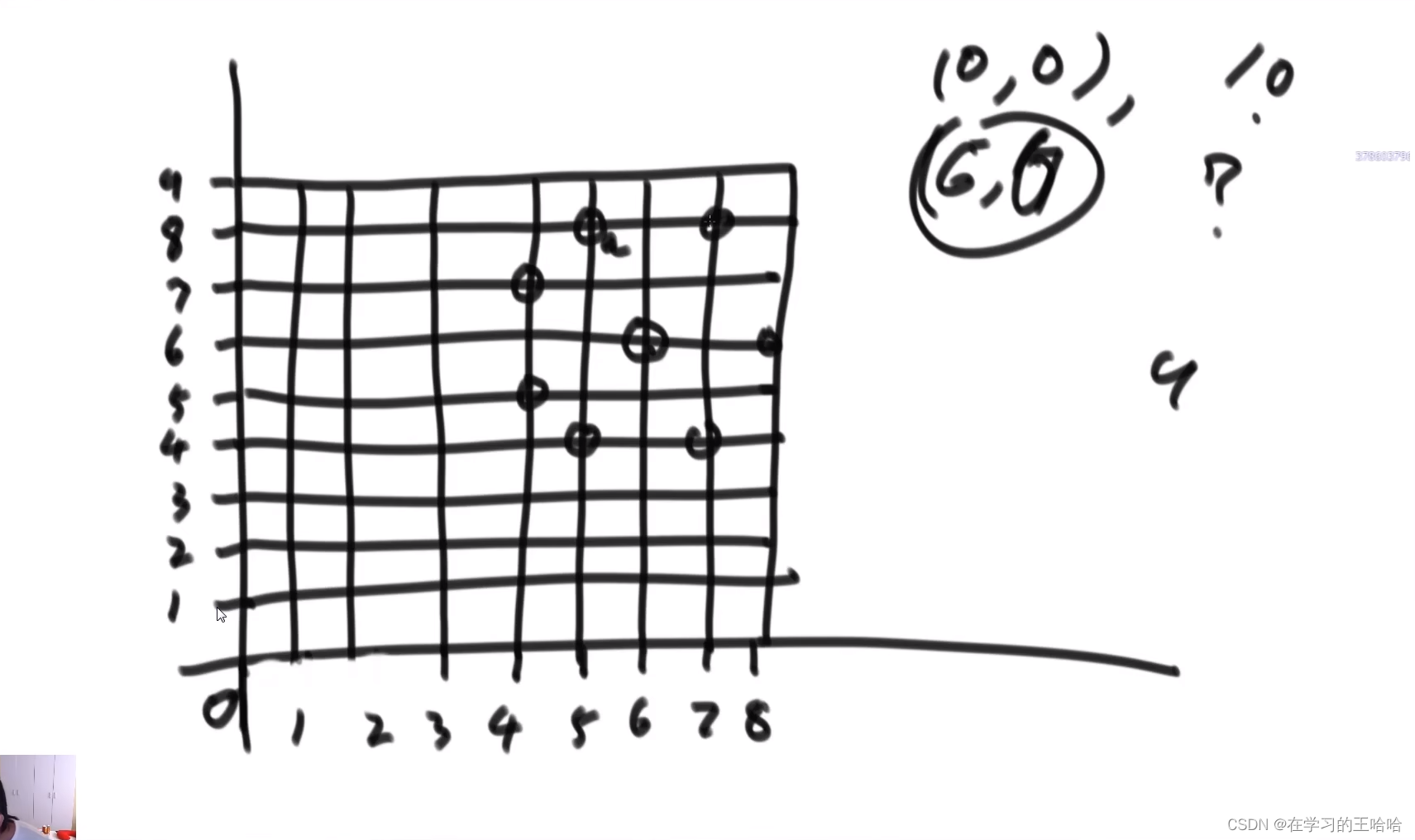
    在这里插入图片描述

    在这里插入图片描述
    step张xy二维表
    在这里插入图片描述

    public static int getWays(int x, int y, int step) {
		return process(x, y, step);
	}
	
	// 潜台词： 从(0,0)位置出发
	//  要去往（x,y）位置， 必须跳 step步
	// 返回方法数 

	public static int process(int x, int y, int step) {
		if (x < 0 || x > 8 || y < 0 || y > 9) {
			return 0;
		}
		if (step == 0) {
			return (x == 0 && y == 0) ? 1 : 0;
		}
		return process(x - 1, y + 2, step - 1)
				+ process(x + 1, y + 2, step - 1)
				+ process(x + 2, y + 1, step - 1)
				+ process(x + 2, y - 1, step - 1)
				+ process(x + 1, y - 2, step - 1)
				+ process(x - 1, y - 2, step - 1)
				+ process(x - 2, y - 1, step - 1)
				+ process(x - 2, y + 1, step - 1);
	}
public static int dpWays(int x, int y, int step) {
		if (x < 0 || x > 8 || y < 0 || y > 9 || step < 0) {
			return 0;
		}
		int[][][] dp = new int[9][10][step + 1];
		dp[0][0][0] = 1;
		for (int h = 1; h <= step; h++) {
			for (int r = 0; r < 9; r++) {
				for (int c = 0; c < 10; c++) {
					dp[r][c][h] += getValue(dp, r - 1, c + 2, h - 1);
					dp[r][c][h] += getValue(dp, r + 1, c + 2, h - 1);
					dp[r][c][h] += getValue(dp, r + 2, c + 1, h - 1);
					dp[r][c][h] += getValue(dp, r + 2, c - 1, h - 1);
					dp[r][c][h] += getValue(dp, r + 1, c - 2, h - 1);
					dp[r][c][h] += getValue(dp, r - 1, c - 2, h - 1);
					dp[r][c][h] += getValue(dp, r - 2, c - 1, h - 1);
					dp[r][c][h] += getValue(dp, r - 2, c + 1, h - 1);
				}
			}
		}
		return dp[x][y][step];
	}

	public static int getValue(int[][][] dp, int row, int col, int step) {
		if (row < 0 || row > 8 || col < 0 || col > 9) {
			return 0;
		}
		return dp[row][col][step];
	}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53

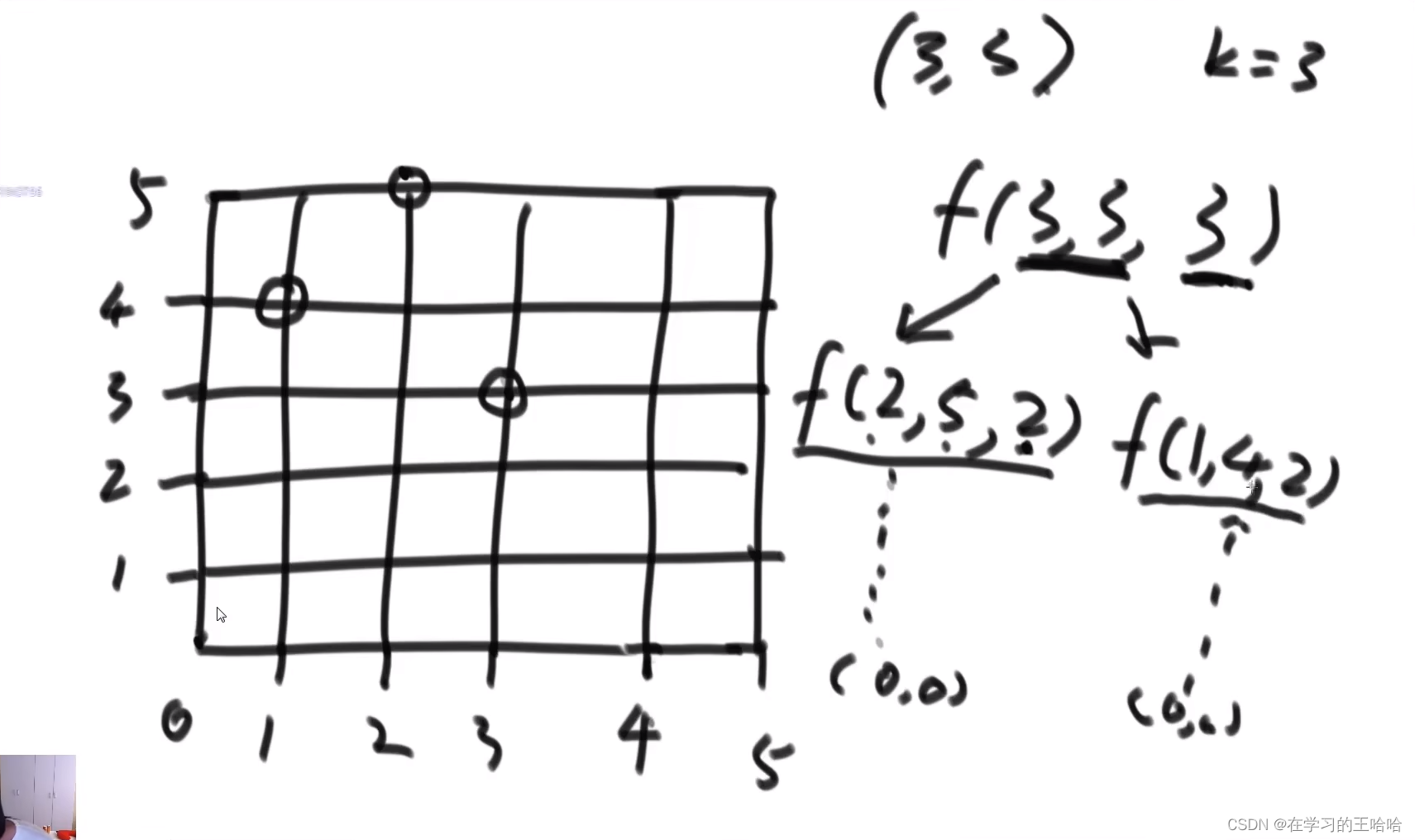
    走格子

    leetcode668
    给行数和列数，表示这个格子有多大。

    行数为5，列数为6。
    Bob所在格子是（a,b）
    Bob所在任何一个点，都等概率随机的向上下左右走。走K步。
    Bob能活下来的概率是多少？

    public static String bob1(int N, int M, int i, int j, int K) {
		long all = (long) Math.pow(4, K);
		long live = process(N, M, i, j, K);
		long gcd = gcd(all, live); // 求一个最大公约数
		return String.valueOf((live / gcd) + "/" + (all / gcd));
	}

	// N * M 的区域，Bob在（row，col）的位置， 走test步之后，获得的生存方法数
	public static long process(int N, int M, int row, int col, int rest) {
		if (row < 0 || row == N || col < 0 || col == M) {
			return 0;
		}
		// row, col 没越界
		if (rest == 0) {
			return 1;
		}
		// 还没走完， row , col 也没越界。
		long live = process(N, M, row - 1, col, rest - 1);
		live += process(N, M, row + 1, col, rest - 1);
		live += process(N, M, row, col - 1, rest - 1);
		live += process(N, M, row, col + 1, rest - 1);
		return live;
	}

	public static long gcd(long m, long n) {
		return n == 0 ? m : gcd(n, m % n);
	}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27

    CoinsWays

    leetcode 518

    一个数组整数，无重复值
    一个位置上的值，代表一个面值
    每一面值的货币无限多。
    组出1000的货币，方法数都多少种。

    递归尝试

    public static int way1(int[] arr, int aim)  {
        return process(arr, 0, aim);
    }

    private static int process(int[] arr, int index, int rest) {
        if (index == arr.length) {
            return rest == 0 ? 1 : 0;
        }
        // arr[index] 0张  1张 。。 不要超过rest的钱数
        int ways = 0;
        for (int zhang = 0; arr[index] * zhang <= rest; zhang++) {
            ways += process(arr, index + 1, rest-arr[index] * zhang);
        }
        return ways;
    }

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15

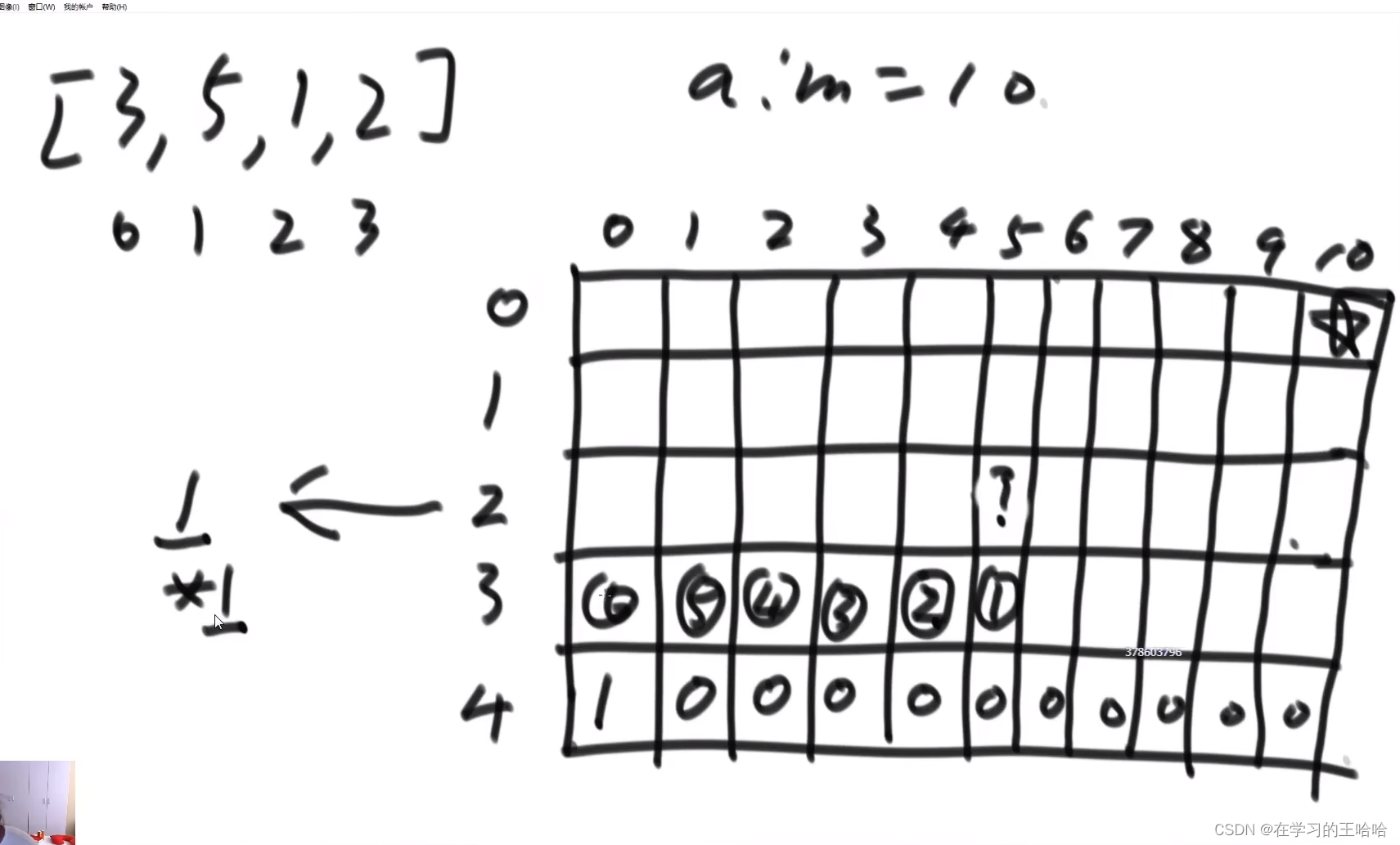
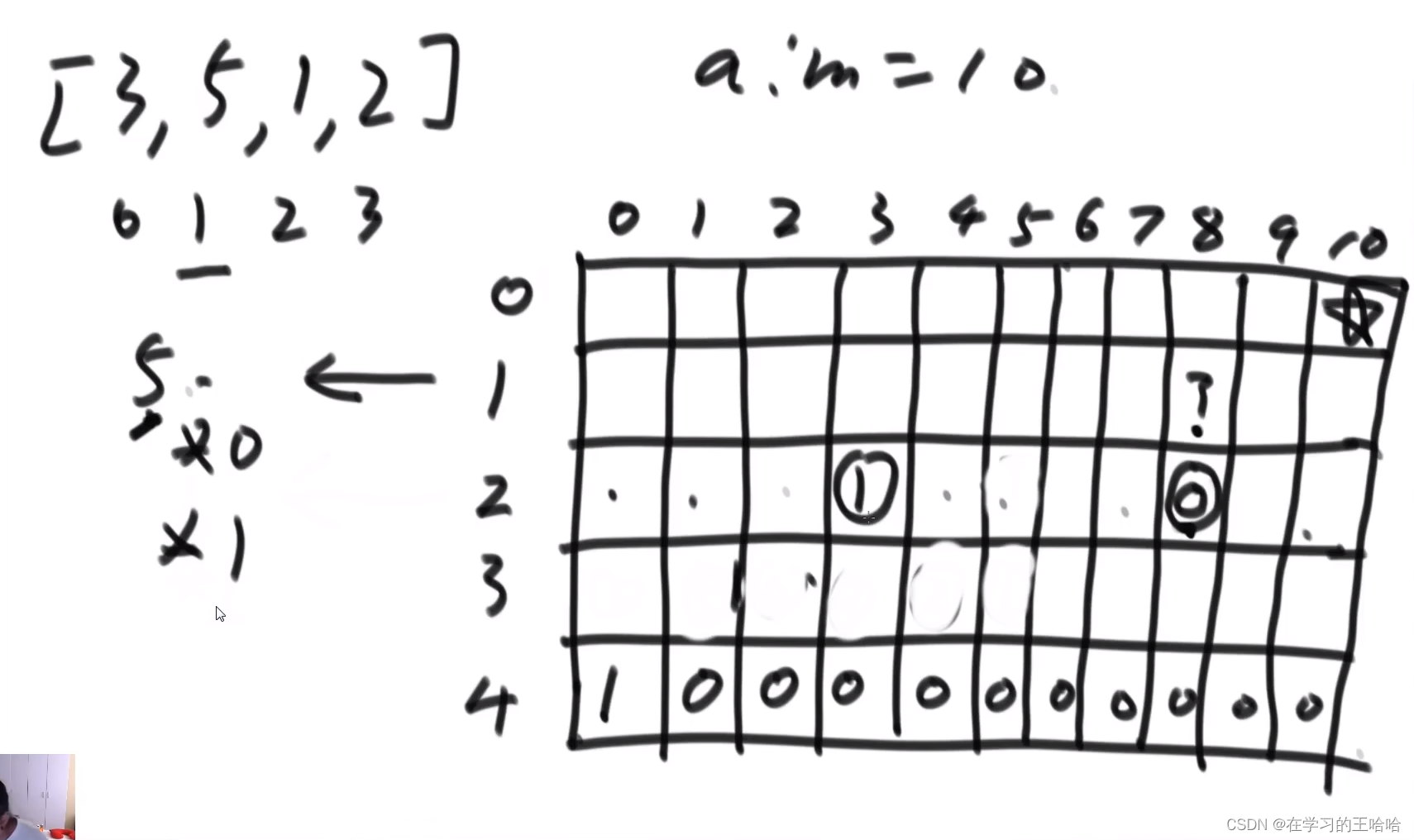
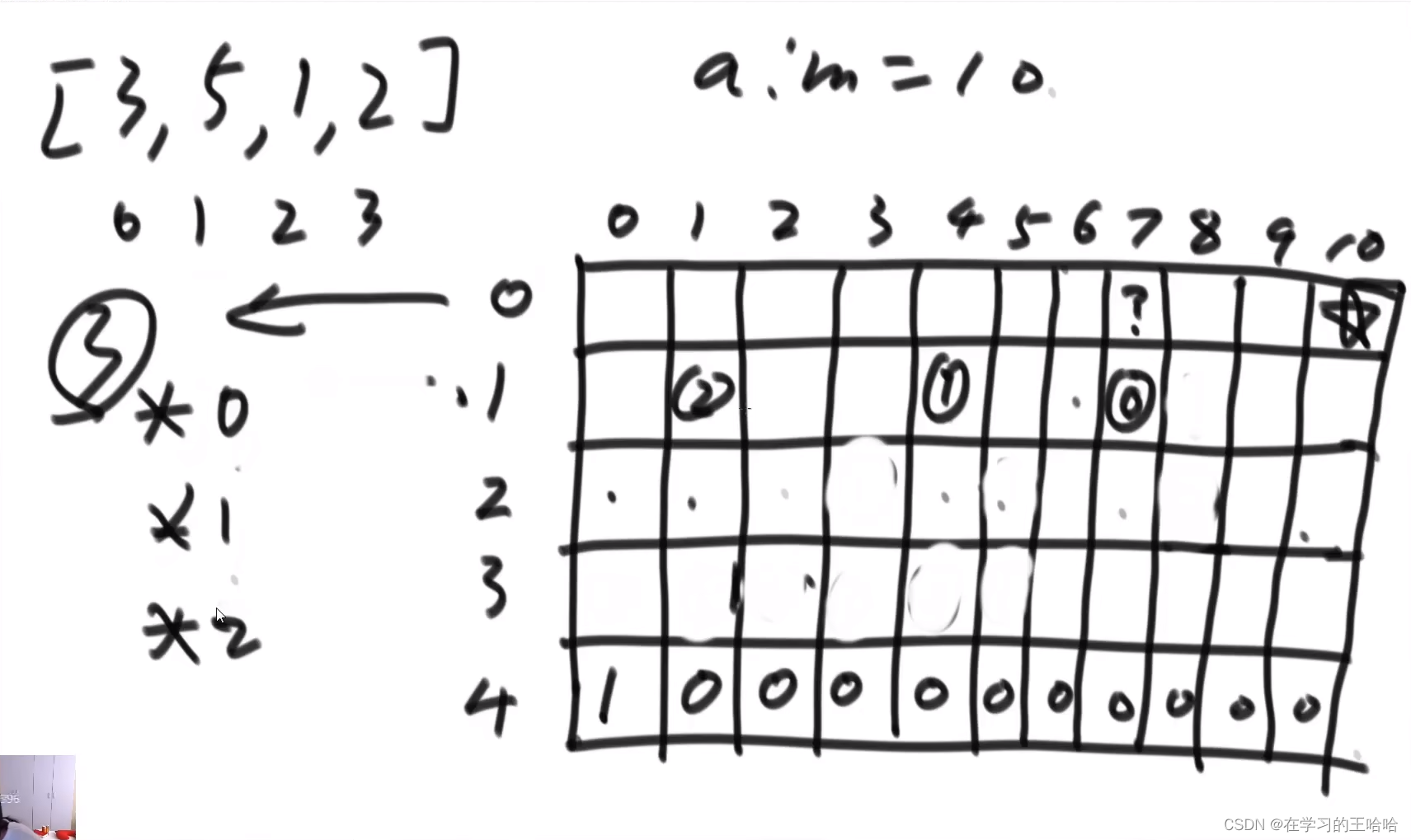
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    不优化的严格表结构

    时间复杂度 N*(aim^2)

     public static int way2(int[] arr, int aim){
        if(arr == null || arr.length ==0){
            return 0;
        }
        int N = arr.length;
        int[][] dp = new int[N+1][aim  + 1];

        dp[N][0] = 1;

        for (int index = N - 1; index >= 0 ; index--) {
            for (int rest = 0; rest <= aim; rest++) {

                int ways = 0;
                for (int zhang = 0; arr[index] * zhang <= rest; zhang++) {
                    ways += dp[index + 1 ] [rest-arr[index] * zhang];
                }
                dp[index][rest] = ways;

            }
        }

        return dp[0][aim]   ;
    }

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23

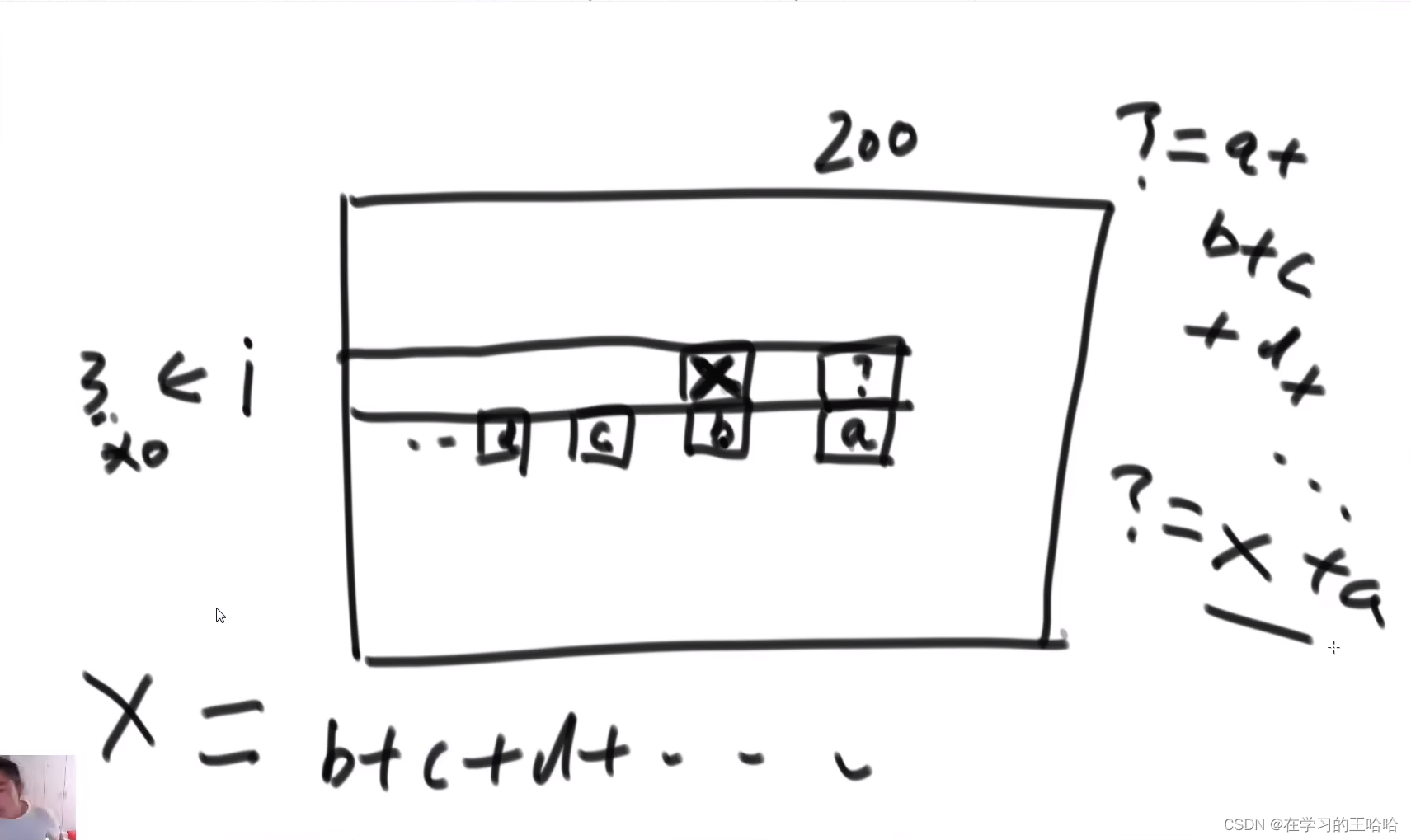
    在这里插入图片描述
    斜率优化
    临近的位置能不能替代 枚举行为。

    public static int way3(int[] arr, int aim){
        if(arr == null || arr.length ==0){
            return 0;
        }
        int N = arr.length;
        int[][] dp = new int[N+1][aim  + 1];

        dp[N][0] = 1;

        for (int index = N - 1; index >= 0 ; index--) {
            for (int rest = 0; rest <= aim; rest++) {

                dp[index][rest] = dp[index+1][rest] ;
                if(rest - arr[index] >= 0 ){
                    dp[index][rest] += dp[index][rest - arr[index]];
                }

            }
        }

        return dp[0][aim]   ;
    }


    // for test
    public static int[] generateRandomArray(int len, int max) {
        int[] arr = new int[(int) (Math.random() * len) + 1];
        for (int i = 0; i < arr.length; i++) {
            arr[i] = (int) (Math.random() * max) + 1;
        }
        return arr;
    }

    public static void main(String[] args) {
        int len = 10;
        int max = 10;
        int testTime = 10000;
        for (int i = 0; i < testTime; i++) {
            int[] arr = generateRandomArray(len, max);
            int aim = (int) (Math.random() * 3 * max) + max;
            if ( way1(arr, aim)  != way2(arr,aim)
                 || way1(arr, aim)  != way3(arr,aim)) {
                System.out.println("ooops!");
                break;
            }
        }
    }

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47

    尝试模型 ： 从左往右，范围 7成以上
    记忆化搜索的方式：
    分析空间格子，严格表结构动态规划。
    可以进一步优化，优化枚举行为。
    在这里插入图片描述
    尝试时，两件事

    1. 尝试的时候每一个可变参数自己维度
    2. 可变参数的个数，最好是整数，最少原则。
  • 相关阅读:
    mock技术在测试中的应用
    STM32智能物流机器人系统教程
    英文科技论文写作与发表-写作实践（第7章）
    Python编程基础：列表的正确使用
    力扣70. 爬楼梯
    LeetCode每日一题(786. K-th Smallest Prime Fraction)
    【BOOST C++】教程3： 数据类型
    十分钟学会angular
    面试官：说说volatile底层实现原理？
    解决mysql表不能查询修改删除等操作并出现卡死
  • 原文地址：https://blog.csdn.net/prague6695/article/details/126115436