[论文阅读] Diverse Image-to-Image Translation via Disentangled Representations

[论文地址] [代码] [ECCV 18]

Abstract

图像到图像的翻译旨在学习两个视觉领域之间的映射。对于许多应用来说，有两个主要的挑战：(1)缺乏对齐的训练对；(2)从单一的输入图像中获得多种可能的输出。在这项工作中，我们提出了一种基于分离表示的方法，在没有配对训练图像的情况下产生不同的输出。为了实现多样性，我们建议将图像嵌入两个空间：一个是捕捉跨领域共享信息的领域不变的内容空间，一个是特定领域的属性空间。使用分解后的特征作为输入，大大减少了模式崩溃。为了处理不配对的训练数据，我们引入了一个新的跨周期一致性损失。定性结果表明，我们的模型可以在广泛的任务中产生多样化和现实的图像。我们通过广泛的评估验证了我们方法的有效性。

Method

本文与MUNIT类似，核心思想是解耦。不同的是，MUNIT是解耦成风格(style)和内容(content)，而本文DRIT解耦的是两个域不同的属性(attribute)与两个域共同的内容(content)，方法流程如下：

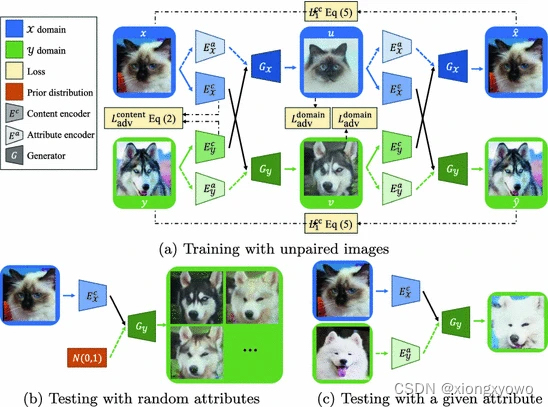
具体损失函数如下：
Disentangle Loss 思路其实挺暴力的，既然两个domain内容应该是共享的，那么仅凭内容向量是无法区分某个图像的domain的，因此单独设计了一个判别器，来促使Encoder编码出判别器无法区分的东西，即"内容"：$$L_{\mathrm{adv}}^{\mathrm{content}}(E_{\mathcal{X}}^c,E_{\mathcal{Y}}^c,D^c)={\mathbb{E}}_x[\frac{1}{2}\log D^c(E_{\mathcal{X}}^c(x))+\frac{1}{2}\log (1-D^c(E_{\mathcal{X}}^c(x)))]+{\mathbb{E}}_y[\frac{1}{2}\log D^c(E_{\mathcal{Y}}^c(y))+\frac{1}{2}\log (1-D^c(E_{\mathcal{Y}}^c(y)))]$$

Cross-Cycle Consistency Loss 其实就是CycleGAN中的loss，图像从X->Y->X应保持一致，从而促使X->Y的这一过程保留原有的内容：$$L_1^{\mathrm{cc}}(G_{\mathcal{X}},G_{\mathcal{Y}},E_{\mathcal{X}}^c,E_{\mathcal{Y}}^c,E_{\mathcal{X}}^a,E_{\mathcal{Y}}^a)={\mathbb{E}}_{x,y}[\Vert G_{\mathcal{X}}(E_{\mathcal{Y}}^c(v),E_{\mathcal{X}}^a(u))-x{\Vert }_1+\Vert G_{\mathcal{Y}}(E_{\mathcal{X}}^c(u),E_{\mathcal{Y}}^a(v))-y{\Vert }_1]$$

Domain Adversarial Loss domain X的图像翻译至domain Y后应该看起来真实，这个是几乎绝大数GAN的基本loss：$$L_{adv}(E_{c\_y},E_{a\_x},G_x,D_x)={\mathbb{E}}_{x,y}[\log D_x(x)+\log (1-D_x(u))]$$

Self-Reconstruction Loss domain X的图像在输入domain X的生成器后需要有能力生自己：$$L_1(G_x,E_{c\_x},E_{a\_x})={\mathbb{E}}_x[\Vert G_x(E_{c\_x}(x),E_{a\_x}(x))-x{\Vert }_1$$

KL Loss 编码得到的属性向量应该尽可能满足先验高斯分布。因此在测试阶段的属性向量就是从先验高斯分布中采样得到的：$$L_{\mathrm{KL}}=\mathbb{E}[D_{\mathrm{KL}}((z_a)\Vert N(0,1))]$$ $$D_{\mathrm{KL}}(p\Vert q)=-\int p(z)\log \frac{p(z)}{q(z)}\mathrm{d}z$$

Latent Regression Loss 将内容向量$c_x$与随机的属性向量z相结合，生成一张新图像后，将其重新使用属性编码器编码，仍能回到自身z。这一点也是保障成功解耦用的。
$$L_{lr}(G_x,G_y)={\mathbb{E}}_x[\Vert G_x(E_{c\_x}(x),z)-z{\Vert }_1+{\mathbb{E}}_y[\Vert G_y(E_{c\_y}(y),z)-z{\Vert }_1]$$