-
【LeetCode-202】快乐数
7.3 快乐数
7.3.1 题目描述
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
示例 1:
输入:n = 19 输出:true 解释: 12 + 92 = 82 82 + 22 = 68 62 + 82 = 100 12 + 02 + 02 = 1- 1
- 2
- 3
- 4
- 5
- 6
- 7
示例 2:
输入:n = 2 输出:false- 1
- 2
提示:
- 1 <= n <= 231 - 1
7.3.2 方法一:用哈希集合检测循环

算法
算法分为两部分,我们需要设计和编写代码。
- 给一个数字 nn,它的下一个数字是什么?
- 按照一系列的数字来判断我们是否进入了一个循环。
第 1 部分我们按照题目的要求做数位分离,求平方和。
第 2 部分可以使用哈希集合完成。每次生成链中的下一个数字时,我们都会检查它是否已经在哈希集合中。
- 如果它不在哈希集合中,我们应该添加它。
- 如果它在哈希集合中,这意味着我们处于一个循环中,因此应该返回 false。
我们使用哈希集合而不是向量、列表或数组的原因是因为我们反复检查其中是否存在某数字。检查数字是否在哈希集合中需要 O(1) 的时间,而对于其他数据结构,则需要 O(n) 的时间。选择正确的数据结构是解决这些问题的关键部分。
class Solution { private int getNext(int n) { int totalSum = 0; while (n > 0) { int d = n % 10; n = n / 10; totalSum += d * d; } return totalSum; } public boolean isHappy(int n) { Set<Integer> seen = new HashSet<>(); while (n != 1 && !seen.contains(n)) { seen.add(n); n = getNext(n); } return n == 1; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
复杂度分析

7.3.3 方法二:快慢指针法
通过反复调用 getNext(n) 得到的链是一个隐式的链表。隐式意味着我们没有实际的链表节点和指针,但数据仍然形成链表结构。起始数字是链表的头 “节点”,链中的所有其他数字都是节点。next 指针是通过调用 getNext(n) 函数获得。
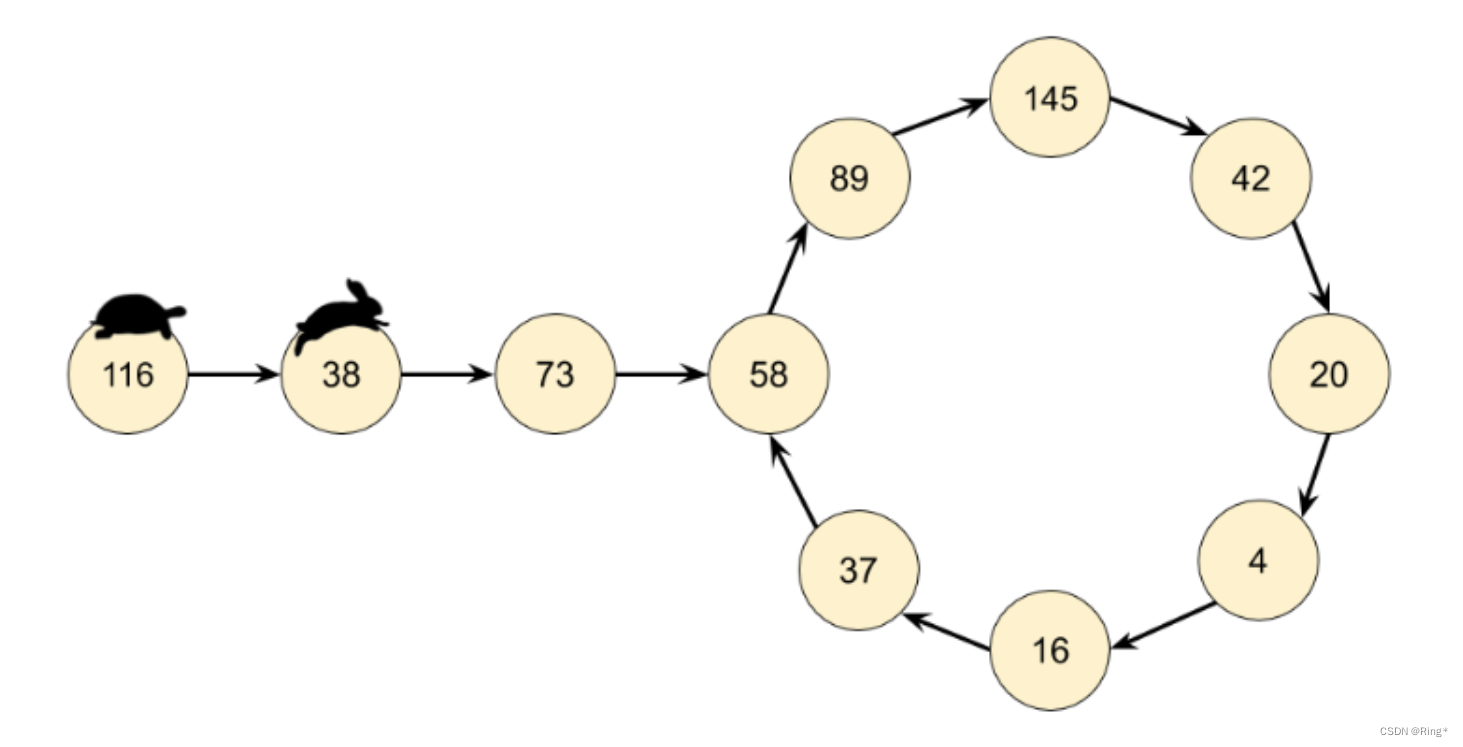
意识到我们实际有个链表,那么这个问题就可以转换为检测一个链表是否有环。因此我们在这里可以使用弗洛伊德循环查找算法。这个算法是两个奔跑选手,一个跑的快,一个跑得慢。在龟兔赛跑的寓言中,跑的慢的称为 “乌龟”,跑得快的称为 “兔子”。
不管乌龟和兔子在循环中从哪里开始,它们最终都会相遇。这是因为兔子每走一步就向乌龟靠近一个节点(在它们的移动方向上)。
算法
我们不是只跟踪链表中的一个值,而是跟踪两个值,称为快跑者和慢跑者。在算法的每一步中,慢速在链表中前进 1 个节点,快跑者前进 2 个节点(对 getNext(n) 函数的嵌套调用)。
如果 n 是一个快乐数,即没有循环,那么快跑者最终会比慢跑者先到达数字 1。
如果 n 不是一个快乐的数字,那么最终快跑者和慢跑者将在同一个数字上相遇。
class Solution { public int getNext(int n) { int totalSum = 0; while (n > 0) { int d = n % 10; n = n / 10; totalSum += d * d; } return totalSum; } public boolean isHappy(int n) { int slowRunner = n; int fastRunner = getNext(n); while (fastRunner != 1 && slowRunner != fastRunner) { slowRunner = getNext(slowRunner); fastRunner = getNext(getNext(fastRunner)); } return fastRunner == 1; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
复杂度分析

7.3.4 方法三:数学
前两种方法是你在面试中应该想到的。第三种方法不是你在面试中会写的,而是针对对数学好奇的人,因为它很有趣。
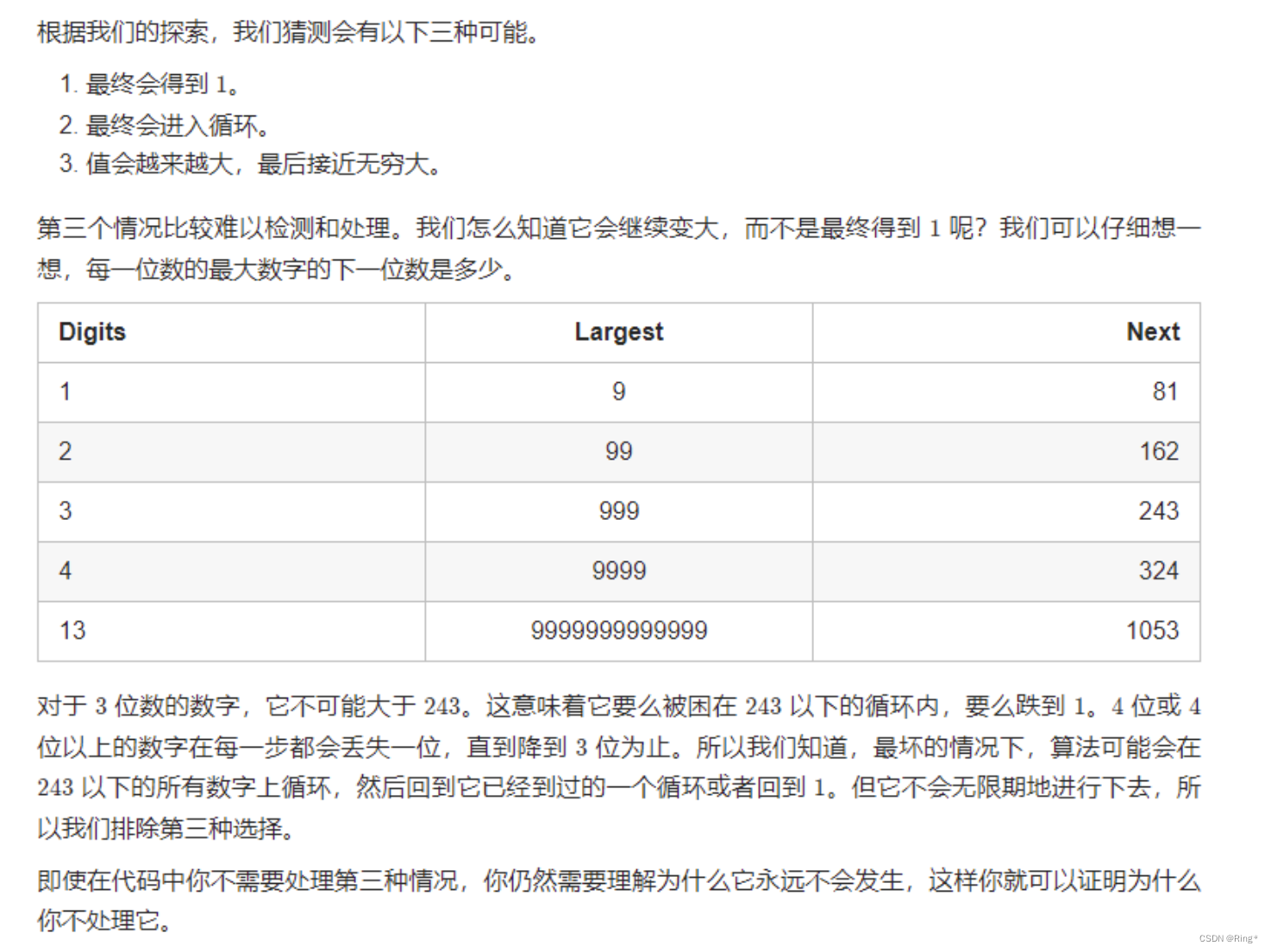
下一个值可能比自己大的最大数字是什么?根据我们之前的分析,我们知道它必须低于 243。因此,我们知道任何循环都必须包含小于 243 的数字,用这么小的数字,编写一个能找到所有周期的强力程序并不困难。
如果这样做,您会发现只有一个循环:44→16→37→58→89→145→42→20→4。所有其他数字都在进入这个循环的链上,或者在进入 1 的链上。
因此,我们可以硬编码一个包含这些数字的散列集,如果我们达到其中一个数字,那么我们就知道在循环中。
算法
class Solution { private static Set<Integer> cycleMembers = new HashSet<>(Arrays.asList(4, 16, 37, 58, 89, 145, 42, 20)); public int getNext(int n) { int totalSum = 0; while (n > 0) { int d = n % 10; n = n / 10; totalSum += d * d; } return totalSum; } public boolean isHappy(int n) { while (n != 1 && !cycleMembers.contains(n)) { n = getNext(n); } return n == 1; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
复杂度分析
- 时间复杂度:O(logn)。和上面一样。
- 空间复杂度:O(1),我们没有保留我们所遇到的数字的历史记录。硬编码哈希集的大小是固定的。
7.3.5 my answer—快慢指针法
class Solution { public boolean isHappy(int n) { int slow_runner = n; int fast_runner = getNextNumber(n); while (fast_runner != 1 && slow_runner != fast_runner){ slow_runner = getNextNumber(slow_runner); fast_runner = getNextNumber(getNextNumber(fast_runner)); } if(fast_runner ==1)return true; else return false; } public static int getNextNumber(int n){ int total = 0; while(n !=0 ){ int a = n % 10; total += a*a; n = n/10; } return total; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
-
相关阅读:
3分钟带你了解微信小程序开发
1、Flowable基础
【进程间通信】进程间通信方式汇总
06【SpringMVC的Restful支持】
Linux 网络命令指南
微信小程序——CSS3渐变
记录一下:基于nginx配置的封禁真实IP
【运维】fstab,systemctl与rc.local启动顺序
2、Linux权限理解
chatgpt赋能python:Python如何快速取出所有元素?
- 原文地址:https://blog.csdn.net/xiaoguanglin/article/details/126241621
