详解欧拉计划第622题：完美洗牌

欧拉计划第622题：完美洗牌

有这样一种洗牌：将牌张平分为两份，左手拿上半部分牌张，右手拿下半部分牌张，然后，将右手的牌严格地交叉到左手的牌张中，也就是右手的第1张牌处于左手的第1张牌后面，右手的第2张牌处于左手的第2张牌后面，依次类推。（注意，这种洗牌法不会改变顶底的两张牌）

记 s(n) 为使牌恢复原状的最少连续洗牌次数，这里的n为偶数。

令人惊奇的是，52张的标准扑克牌只需8次洗牌就可以恢复原状，因此有：s(52) = 8，同样可以验证，86张的扑克牌也只需8次洗牌恢复原状，将所有满足s(n)=8的n求和可以得到412。

强烈推荐先不要直接看解题过程，先自己动手尝试一下。

解题过程：

第一步，用程序实现洗牌过程

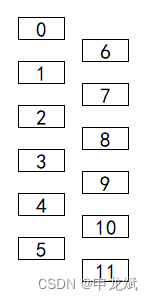
假设有12张牌，编号分别从0到11，初始时按顺序排列，一次洗牌后变为0，6，1，7，2，8，3，9，4，10，5，11，示意图如下。

def perfect_shuffle