买口罩（0-1背包）

链接

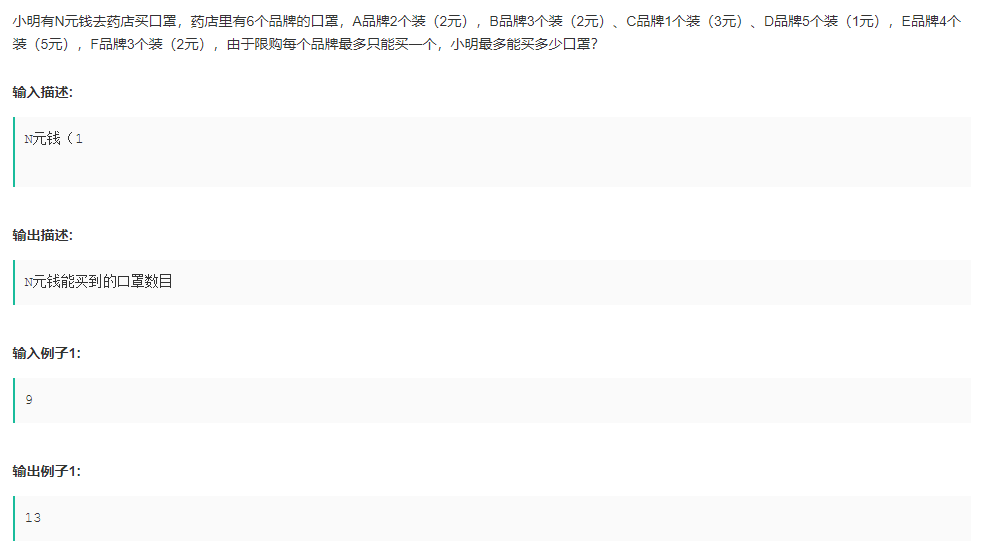
题目：

思路： 0-1 背包

背包两个属性：容量W和N个物品（N个数一般等于物品数量，即 状态 i ）
限定的是什么钱，即钱就是限定的容量W，对应物品单价就是wt
求最多买多少口罩，即口罩的个数就是val值；

初始化 dp[N+1][W+1]，

dp定义：最终所求为 dp[N][W]即对前 i 个物品进行选择，在容量为 w时，可以装的最大价值是 dp[i][w]；

basecase：
base case 就是 dp[0][…] = dp[…][0] = 0，即没有物品和没有容量时，背包装的价值为0；但数组会自动初始化为0；

状态： i 为物品序号， w为每种容量；

状态转移：
求以下两种的最大值：
1.不装入 i 物品，dp=dp[i-1][w] ;
2.装入 i 物品，dp=dp[i-1][w-wt[i]]+val[i] ，即前i-1个物品相当于放到了容量为 w - wt[i-1]]的背包里！

注意：
i =0 是base case , 所以遍历状态要从 i=1 开始！

import java.util.Scanner;
public class Main{
    public static void main(String[] args){
        Scanner in=new Scanner(System.in);
        int W=in.nextInt();
        // 限定了N元，即价格是背包容量
        int[] wt={0,2,2,3,1,5,2};
        // 求最多多少口罩，即口罩个数是价值
        int[] val={0,2,3,1,5,4,3};
        int N=6;
        int[][] dp=new int[n+1][W+1]; // 会初始化为全0
        // i=0是base case 
        for(int p=0;p<=W;p++){
            dp[0][p]=0; //没有物品
        }
        for(int q=0;q<=N;q++){
            dp[q][0]=0;//没有容量
        }
        //
        for(int i=1;i<=N;i++){//遍历每个物品（序号）
            for(int w=0;w<=W;w++){ //遍历每种容量大小
                if(w<wt[i]){ //当前容量w小于了物品i需要的容量，则一定不放背包
                    dp[i][w]=dp[i-1][w];
                }else{ //  放入和不放入，选最大
                    dp[i][w]=Math.max( dp[i-1][w] , dp[i-1][w-wt[i]]+val[i]);
                }
            }                 
        }
        System.out.println(dp[N][W]);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31