1、内容简介

略
494-可以交流、咨询、答疑

2、内容说明

3 SMITH控制

3.1 SMITH预测原理

 在控制系统中，纯滞后的环节可以出现在不同的位置，它们对过程调节的影响是不同的。以纯滞后单回路控制系统为例，说明了如何减少纯滞后对系统的影响。其结构图如下:

   R(s) Y(s)

           -     -  

图3.1纯滞后补偿的结构图

Gc(s)为普通调节器的传递函数，G(s) exp(-s)为对象的传递函数。则在没有滞后补偿的控制系统的传递函数为:      

                                (3-1)

在闭环传递函数的分母中，还有纯滞后环节exp(一二)，这将导致稳定的减少，当足够大的时候，系统将是不稳定的。为了使系统得到充分补偿，应该有:  

                                    (3-2)

经过完全补偿后，完全补偿后的闭环传递函数为:

                                   (3-3)

它消除了纯滞后部分对控制系统的影响，因为公式中的exp(-s)在闭环控制回路之外，不影响系统的稳定性，拉普拉斯变换定理表明，exp(-s)仅仅为控制作用在时间坐标上推移了一个时间z，而控制系统的过渡过程及其他性能指标都与对象特性为G(s)时完全相同。此种补偿为SMITH预估补偿。

3.2 SMITH预估补偿结构的改进

由于被控对象的参数是会改变的，纯滞后环节通常会用近似式表达式表示，使得出现了预估补偿器不能实现完全补偿，系统的稳定性会变差，为了提高系统的稳定性，将滤波器加入到SMITH预估值和实际系统的输出值的误差回路中，以此增加系统的稳定性。其结构图如下:

图3.2改进的SMITH预估补偿

在这里，GF (s)取为加权平均滤波器，此滤波器的特征:

方法:数据在不同的时间加以不同的权，通常越接近现时刻的数据，权值取得越大。新的采样值权系数越大，灵敏度越高，但信号平滑度越低。

优点:适用于较大纯滞后时间常数的对象和较短的采样周期的系统。

缺点:对于纯滞后时间常数较小，采样周期较长，变化缓慢的信号不能迅速反应系统当前所受干扰的严重程度，滤波效果差。

    由于中央空调的湿度控制通常是存在大滞后，滞后时间长，采样周期不长，故此滤波器适用。

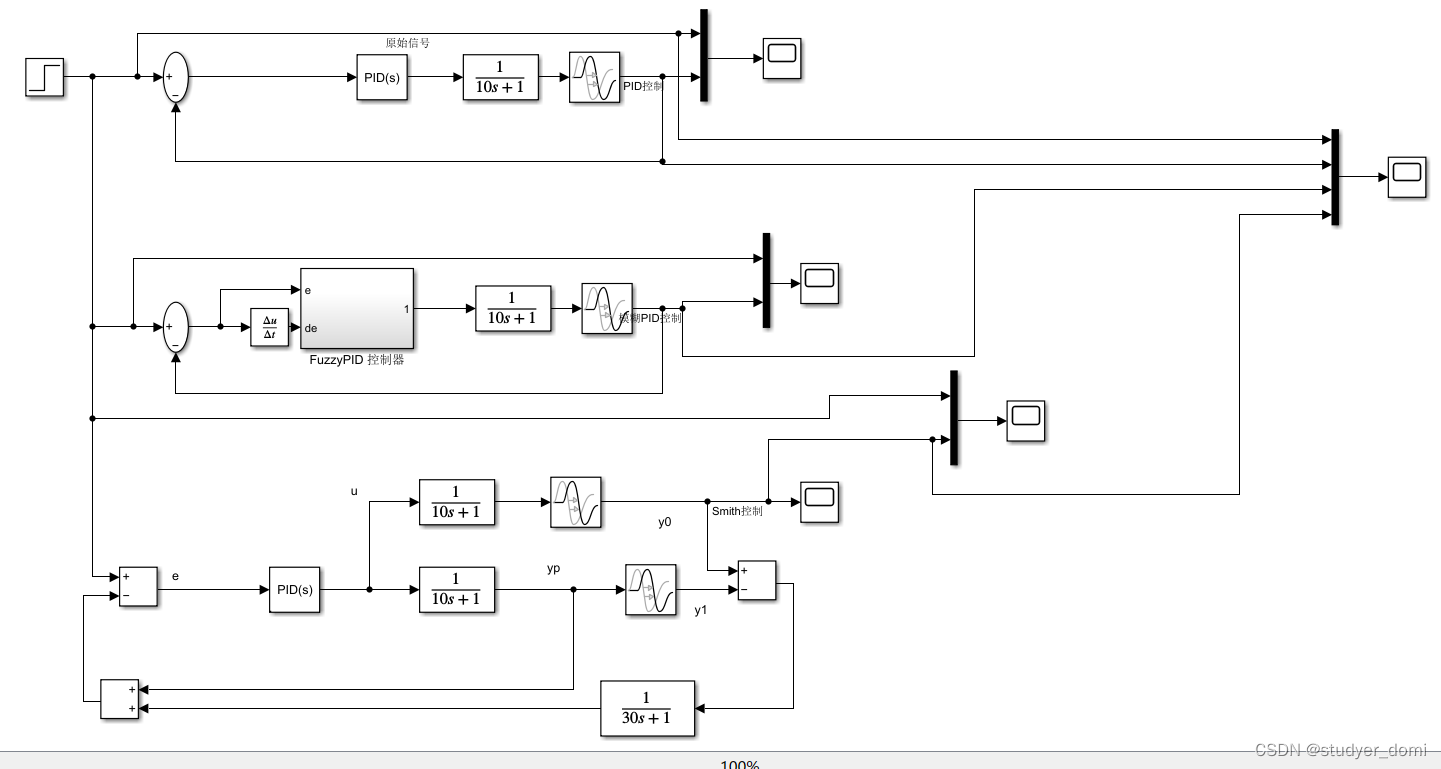
3、仿真分析

略

4、参考论文

略