-
矩阵分析与应用-16-广义逆矩阵
目录
左逆矩阵与右逆矩阵
满足
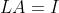 ,但不满足
,但不满足 的矩阵
的矩阵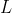 称为矩阵
称为矩阵 的左逆矩阵(left inverse)。
的左逆矩阵(left inverse)。满足
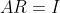 ,但不满足
,但不满足 的矩阵称为矩阵
的矩阵称为矩阵 的右逆矩阵(right inverse)o
的右逆矩阵(right inverse)o仅当
 时,矩阵
时,矩阵 T可能有右逆矩阵。
T可能有右逆矩阵。广义逆矩阵的定义及性质
线性方程
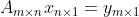 称为一致方程,若矩阵
称为一致方程,若矩阵 的行之间存在的线性关系也存在于向量
的行之间存在的线性关系也存在于向量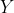 的对应元素中。
的对应元素中。令
 是一个m x n矩阵,具有任意秩。矩阵
是一个m x n矩阵,具有任意秩。矩阵 的广义逆矩阵是-个n x m矩阵G,并使得当
的广义逆矩阵是-个n x m矩阵G,并使得当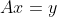 为一致方程时,
为一致方程时,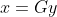 是线性方程
是线性方程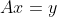 的解。
的解。一致方程
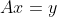 对y≠0有解
对y≠0有解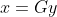 ,当且仅当AGA = A。
,当且仅当AGA = A。m × n矩阵A的广义逆矩阵是一个满足
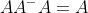
的nx m矩阵
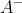 。
。m x n矩阵A的广义逆矩阵是满足下列条件之一的n × m 矩阵
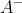
(1)
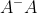 为幂等矩阵,且 rank(.
为幂等矩阵,且 rank(.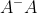 ) rank(
) rank( ):
):(2)
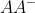 是幂等矩阵,且rank(
是幂等矩阵,且rank(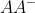 ) =rank(
) =rank( )。
)。性质:
方程
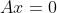 的解与矩阵
的解与矩阵 的任意行正交,并且线性无关。
的任意行正交,并且线性无关。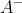 存在
存在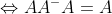
定理1:一线性方程组可以求解,当且仅当这些方程为一致方程。
定理2:线性方程
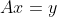 是一致的,当且仅当增广矩阵
是一致的,当且仅当增广矩阵 的秩等于矩阵
的秩等于矩阵 的秩,即
的秩,即 。
。广义逆矩阵的计算
令
 具有秩r。若
具有秩r。若 ,其中,
,其中,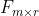 的秩为r (满列秩矩阵),且
的秩为r (满列秩矩阵),且 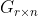 的秩也为r(满行秩矩阵),则称
的秩也为r(满行秩矩阵),则称 为矩阵A的满秩分解(full-rank decomposition)。
为矩阵A的满秩分解(full-rank decomposition)。一个秩为r的mx n矩阵A可以分解为
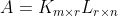
式中,K和L分别具有满列秩和满行秩。
若矩阵
 具有秩r,且其满秩分解为
具有秩r,且其满秩分解为 ,其中,
,其中,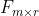 为满列秩
为满列秩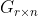 为满行秩,则
为满行秩,则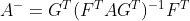
是
 的一个广义逆矩阵。
的一个广义逆矩阵。 矩阵的满秩分解算法
1.利用行初等变换将矩阵A化为阶梯型
![A\xrightarrow[E_1]{}[]\xrightarrow[E_2]{}...\xrightarrow[E_k]{}\begin{bmatrix} G_{r\times n}\\ O_{(m-r)\times n} \end{bmatrix}](https://1000bd.com/contentImg/2022/08/12/190935145.gif)
2.对单位矩阵执行逆行初等变换,得到逆矩阵
![I\xrightarrow[E_k^{-1}]{}[ ]\xrightarrow[E_{k-1}^{-1}]{}....\xrightarrow[E_1^{-1}]{}[]=P^{-1}](https://1000bd.com/contentImg/2022/08/12/190936004.gif)
3.利用逆矩阵
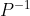 的前r列构造矩阵F。
的前r列构造矩阵F。4.书写满秩分解结果
 。
。广义逆矩阵的计算
1.计算矩阵
 的满秩分解
的满秩分解 。
。2.求广义逆矩阵
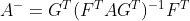 。
。一致方程的最小范数解
令n x m 矩阵
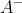 是m×n矩阵
是m×n矩阵 的任意一个广义逆矩阵,则
的任意一个广义逆矩阵,则(1)齐次方程
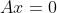 的一个通解为
的一个通解为 ,其中,z是n×1任意向量。
,其中,z是n×1任意向量。(2非齐次方程
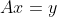 为-致方程的充分必要条件是
为-致方程的充分必要条件是
(3)非齐次方程Aa = g 的一个通解为

式中,z为n×1任意向量。
伴随矩阵具有以下性质
(1)

(2)

(3)

(4)
 (若A为实矩阵)或
(若A为实矩阵)或 (若A为复矩阵)
(若A为复矩阵) 是一致方程
是一致方程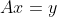 的最小范数解,当且仅当
的最小范数解,当且仅当
非一致方程的最小二乘解
令G是某个矩阵,则
 是非一致方程
是非一致方程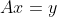 的最小二乘解,当且仅当
的最小二乘解,当且仅当
或

-
相关阅读:
【虹科案例】极高的精度水平——虹科数字化仪在大型强子对撞机机器保护系统中的应用
VS2017下第一个C#控制台程序helloworld
Java多线程(5):CAS
我在滴滴做开源
解决SQL错误(208):对象名‘string_split‘无效的正确方法,亲测有效!!!
ssh连win10报错:Permission denied (publickey,keyboard-interactive).
单链表OJ题(2):反转链表(三指针法)、找中间节点(快慢指针)
ORACLE 基础
iOS中的锁
国外发达国家码农是真混得好么?
- 原文地址:https://blog.csdn.net/Xiao__fly/article/details/126234564