【考研】数据结构考点——希尔排序

前言

本文内容源于对《数据结构（C语言版）》（第2版）、王道讲解学习所得心得、笔记整理和总结。

插入排序的三种方法：直接插入排序、折半插入排序和希尔排序。直接插入排序可基于顺序表或链表操作，但后两种插入方法只能基于顺序存储结构。

本文内容主要针对希尔排序。分析算法，并结合例子，以图文形式讲解希尔排序的过程。

可搭配以下链接一起学习：

【考研】数据结构考点——直接插入排序_住在阳光的心里的博客-CSDN博客

【考研复习：数据结构】查找（不含代码篇）_住在阳光的心里的博客-CSDN博客

目录

前言

一、基本概念

二、算法步骤

三、算法描述

四、算法分析及算法特点

（一）算法分析

（二）算法特点

五、练习

---

一、基本概念

直接插入排序，当待排序的记录个数较少且待排序序列的关键字基本有序时，效率较高。希尔排序基于以上两点，从“减少记录个数”和“序列基本有序”两个方面对直接插人排序进行了改进。

希尔排序，又称缩小增量排序。

实质上是采用分组插入的方法。先将整个待排序记录序列分割成几组，从而减少参与直接插入排序的数据量，对每组分别进行直接插入排序，然后增加每组的数据量，重新分组。

这样当经过几次分组排序后，整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。

希尔对记录的分组，不是简单地“逐段分割"，而是将相隔某个“增量”的记录分成组。它并不能保证每趟排序至少能将一个元素放到其最终位置上。

二、算法步骤

1、 第一趟取增量 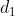 ( 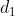< n) 把全部记录分成  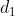个组，所有间隔为  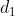的记录分在同一组，在
各个组中进行直接插入排序。

2、第二趟取增量 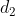  (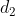 < 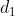)，重复上述的分组和排序。

3、依次类推，直到所取的增量 ，所有记录在同组中进行直接插入排序为止。

注意：一般采用希尔提出的：(最后一个增量为1)

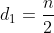
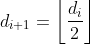 （也可以向上取整）

可结合“五、练习”（本文最下方例子）学习，有搭配图文，详细举例讲解。

三、算法描述

希尔排序的算法实现如代码所示。

预设好的增量序列保存在数组 dt[0...t-1] 中，整个希尔排序算法需执行 t 趟。

由于直接插入排序可看成一趟增量是 1 的希尔排序，改写后可得到一趟希尔排序算法ShellInsert。

在ShellInsert中，具体改写主要有两处:

1、前后记录位置的增量是 dk，而不是1;

2、r[0] 只是暂存单元，不是哨兵。当 j≤0 时，插入位置已找到。

//对顺序表L做一趟增量是dk的希尔插入排序
void ShellInsert (SqList &L，int dk)
{
    for (int i = dk + 1; i <= L.length; ++i){
        if(L.r[i].key < L.r[i-dk].key){    //需将 L.r[i] 插入有序增量子表
            L.r[0] = L.r[i];    //暂存在L.r[0]
 
            for(j = i - dk; j >0 && L.r[0].key < L.r[j].key; j -= dk){
                L.r[j+dk] = L.r[j];   //记录后移，直到找到插入位置
            }
            L.r[j+dk] = L.r[0];    //将 r[0] 即原 r[i] ，插入到正确位置 
        }
    }
}
 
 
//按增量序列 dt[0..t-1] 对顺序表 L 作趟希尔排序
void Shellsort(SqList &L, int dt[], int t)
{
    for(int k = 0; k < t; ++k)
       ShellInsert(L, dt[k]);    //一趟增量为 dt[t] 的希尔插入排序 
}
 
 

四、算法分析及算法特点

（一）算法分析

1、时间复杂度

当增量大于1时，关键字较小的记录就不是步一步地挪动， 而是跳跃式地移动，从而使得在进行最后趟增量为 1 的插入排序中，序列已基本有序，只要做记录的少量比较和移动即可完成排序，因此希尔排序的时间复杂度较直接插人排序低。

但要具体进行分析，则是一个复杂的问题，因为希尔排序的时间复杂度是所取“增量”序列的函数，这涉及一些数学 上尚未解决的难题。因此，到目前为止尚未有人求得一种最好的增量序列，但大量的研究已得出一些局部的结论。

如有人指出，当增量序列为  时，希尔排序的时间复杂度为 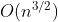，其中 t 为排序趟数， 。在最坏情况下，希尔排序的时间复杂度为 。

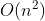还有人在大量的实验基础上推出：当n在某个特定范围内，希尔排序所需的比较和移动次数约为 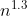，当  时，可减少到 。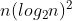

2、空间复杂度

从空间来看，希尔排序和前面两种排序方法样，也只需要个辅助空间 r[0]，空间复杂度为 。
 

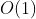（二）算法特点

1、记录跳跃式地移动导致排序方法是不稳定的。

2、只能用于顺序结构，不能用于链式结构。

3、增量序列可以有各种取法。但应该使增量序列中的值没有除1之外的公因子， 并且最后一个增量值必须等于1。

4、记录总的比较次数和移动次数都比直接插人排序要少，n 越大时，效果越明显。所以适
合初始记录无序、n 较大时的情况。
 

五、练习

1、已知待排序记录的关键字序列为{49，38，65，97，76，13，27，49 , 55，04}，请给出用希尔排序法进行排序的过程。

解：希尔提出：d1 = n/2 = 10/2= 5， d2 = d1/2(向上取整)= 5/2 = 3，d3 = 1（最后一个增量为1）

步骤分析如下：

1、第一趟取增量 d1 = 5，所有间隔为 5 的记录分在同一组，全部记录分成 5 组，在各个组中分别进行直接插入排序。

2、第二趟取增量d2 = 3，所有间隔为 3 的记录分在同一组，全部记录分成3组，在各个组中分别进行直接插入排序。

3、第三趟取增量d3 = 1，对整个序列进行一趟直接插入排序，排序完成。

 所以，最后的排序结果为 04、13、27、38、49、49、55、65、76、97

2、对序列 {15，9，7，8，20，-1，4} 用希尔排序方法排序，经一趟后序列变为 {15，-1，4，8，20，9，7} ，则该次采用的增量是（     B    ）

A. 1                        B. 4                          C. 3                               D. 2

解：对比 {15，9，7，8，20，-1，4} 和 {15，-1，4，8，20，9，7}，发现变动位置有9和-1，7和4，所以增量为4。

3、用希尔排序方法对一个数据序列进行排序时，若第1趟排序结果为 9, 1, 4, 13, 7, 8, 20, 23, 15，则该趟排序采用的增量（间隔）可能是(     B    )。

A. 2                       B. 3                          C. 4                               D. 5

解：由第1趟排序结果为 9, 1, 4, 13, 7, 8, 20, 23, 15，知第二个位置为1，所以该希尔排序是由小到大的排序。

从第一个位置“ 9 ”，往后数，比 9 大的数为 13，可知此时增量为 3。

假设由此推论下来，第二个位置“ 1 ”，增量为 3 时，对比 7，1 比 7 小，满足直接插入排序结果。

第二个位置“ 4 ”，增量为 3 时，对比 8，4 比 8 小，满足直接插入排序结果。

……

所以得出结论，增量可能是 3 。

​