算法---------空间复杂度

空间复杂度：

空间开销（内存开销）与问题规模n之间的关系

例1：

我们依然选择上篇文章中将时间复杂度用到的实例：

void loveyou(int n)//n为问题规模
{
	int i = 1;
	while (i <= n)
	{
		i++;
		printf("I LOVE YOU%d", i);
	}
	printf("I LOVE YOU More than %d\n", n);
}
1
2
3
4
5
6
7
8
9
10

将该程序放入计算机中，它在内存中，存储形式如下所示：

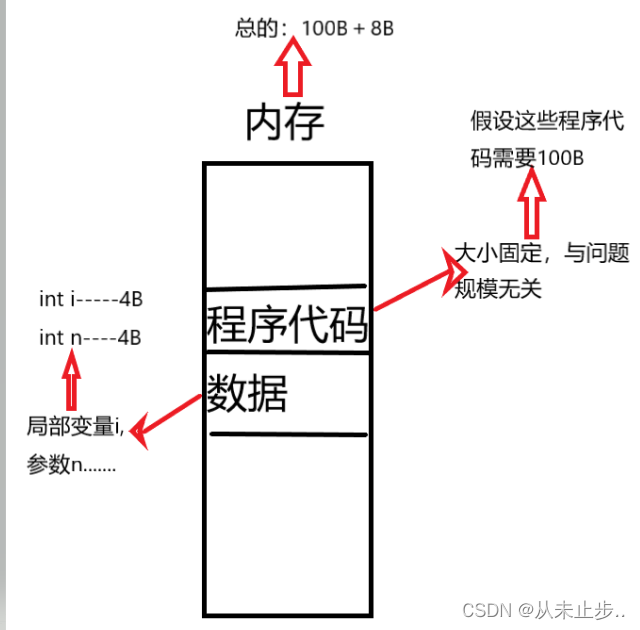
由此可知，无论问题规模怎么变化，算法运行所需的内存空间都是固定的常量，算法空间复杂度为S(n)=O(1),这也被称为算法原地工作。

算法原地工作是指：算法所需内存空间为常量。

但并不都是无论问题规模怎么变化，算法运行所需的内存空间都是固定的常量的这种情况。

例2：

我们依然选择上篇文章中将时间复杂度用到的实例：

void loveyou(int n)
{
	printf("I LOVE YOU More than %d\n", n);
	int i = 1;
	while (i < n)
	{
		if (Flag[i] == n)
			printf("I LOVE YOU%d\n", i);
	}
}
//Flag数组乱序存放1-n这些数
int Flag[n]={1.....n};
loveyou(Flag,n);
1
2
3
4
5
6
7
8
9
10
11
12
13

将该程序放入计算机中，它在内存中，存储形式如下所示：

此时，空间复杂度就和时间规模n有关联，由此可得算法空间复杂度为S（n）=O(4n+8)=O(n)

例3：

void test(int n)
{
	int flag[n][n];
	int i;
	......
}
1
2
3
4
5
6

对于这个程序代码，我们依然可以根据上面的分析过程进行分析，不过需要提醒的是：

int flag[n][n];//所占内存空间为：4n*n,而不是16n*n
//原因：该数组被定义为整形数组，那么该数组一个元素所占据的空间是4B,数组元素的个数有n*n个
1
2

由此可得该算法的空间复杂度为：S(n)=4nn+8=O(nn)

例4：

void test(int n)
{
	int flag[n][n];
	int other[n];
	int i;
}
1
2
3
4
5
6

对于这个程序代码，我们分析得出算法空间复杂度为：S(n)=4nn+n+8=O(nn)+O(n)+O(1)=O(n*n).

总结：

程序代码在内存中所占的空间是大小不变的，因此在分析空间复杂度时，只需要分析变量所占的空间，计算出算法空间复杂度后，处理方式依然和时间复杂度相同，保留高阶，忽略低阶（不懂得可以参考上篇文章）

函数递归调用带来的内存开销：

每次调用所需内存空间的大小相同：

举例：

void loveyou(int n)
{
	int a, b, c;//每次调用，a,b,c的值虽然没有改变，但存储位置法会随着n变化
	if (n > 1)
	{
		loveyou(n - 1);
	}
	printf("I love you %d\n", n);
}
int main()
{
	loveyou(5);
}
1
2
3
4
5
6
7
8
9
10
11
12
13

分析过程如下：
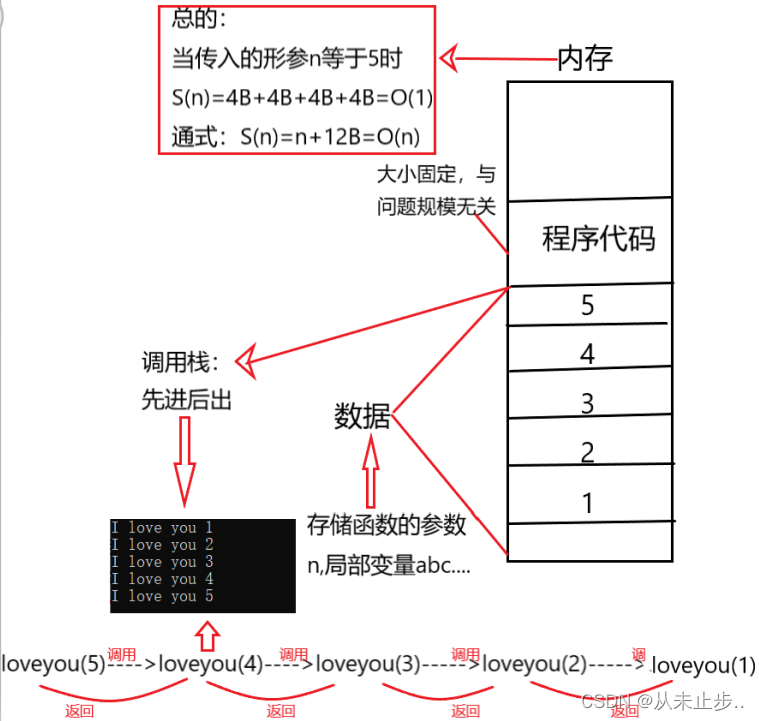由此，我们可以得出一个结论：空间复杂度=递归调用的深度

void loveyou(int n)
{
	int flag[n];
	if (n > 1)
	{
		loveyou(n - 1);
	}
	printf("I love you %d\n", n);
}
int main()
{
	loveyou(5);
}
1
2
3
4
5
6
7
8
9
10
11
12
13

与上面那个例子不同的是：该实例中的int flag[n]中的n,也会随着调用次数而变化,因此，每一级数组的长度是不同的，这也导致，每一级的调用空间是不同的。

因此，各级调用的空间复杂程度为:1+2+3+4+5+…+n=[n(1+n)]/2=1/2nn+1/2n,故S(n)=O(n*n).