中缀表达式：a+b
前缀表达式（波兰式）：运算符位于两个操作数之前，如+ab
后缀表达式（逆波兰式）：运算符位于两个操作数之后，如ab+

---

1.【手算】根据表达式，计算值

1.1 后缀表达式

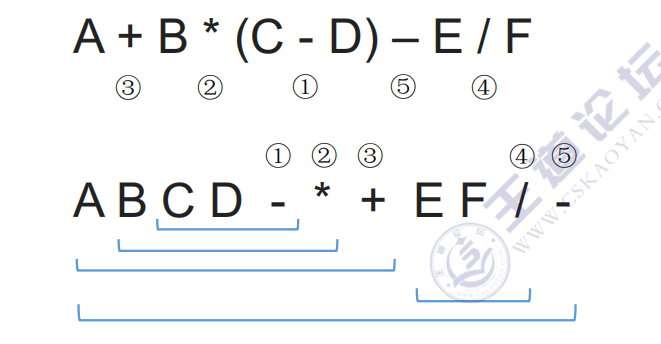
从左往右扫描，每遇到一个运算符，就让运算符前面最近的两个操作数执行对应运算，合体为一个操作数

例子1：

例子2：

---

1.2 前缀表达式

从右往左扫描，每遇到一个运算符，就让运算符后面最近的两个操作数执行对应运算，合体为一个操作数

例子1：

---

1.3 中缀表达式

跟小学学的加减乘除一样
如：

---

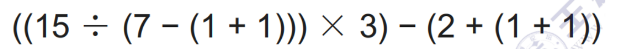
2.【用栈算】根据表达式，计算值

2.1 后缀表达式

用栈实现后缀表达式的计算：
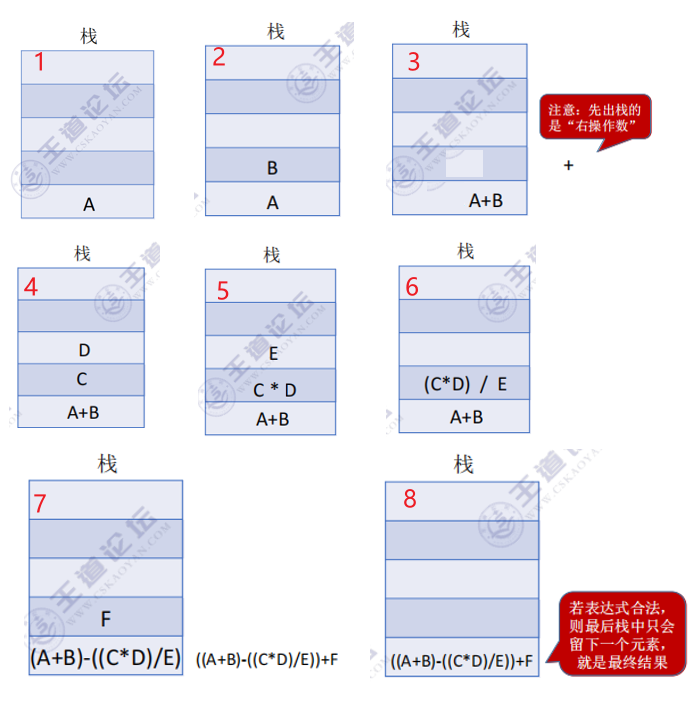
①从左往右扫描后缀表达式，直到处理完所有元素
②若扫描到操作数，则 压入栈，并回到①；否则执行③
③若扫描到运算符，则弹出两个栈顶元素，执行相应运算，运算结果压回栈顶，回到①

例子1：

---

2.2 前缀表达式

用栈实现前缀表达式的计算：
①从右往左扫描前缀表达式，直到处理完所有元素
②若扫描到操作数，则 压入栈，并回到①；否则执行③
③若扫描到运算符，则弹出两个栈顶元素，执行相应运算，运算结果压回栈顶，回到①

具体和2.1 后缀表达式一样，只不过是扫描字符方向变了–>从右到左

---

2.3 中缀表达式

3.2中缀转后缀 + 2.1后缀表达式求值——>两个算法的结合

用栈实现中缀表述式的计算，需先明白下面两个算法：
本博客：3.2中缀转后缀
本博客：2.1后缀表达式求值

用栈实现中缀表达式的计算：

1. 初始化两个栈，操作数栈和运算符栈
2. 若扫描到操作数，压入操作数栈
3. 若扫描到运算符或界限符，则按照“中缀转后缀”相同的逻辑压入运算符栈（期间也会弹出运算符，每当弹出一个运算符时，就需要再弹出两个操作数栈的栈顶元素并执行相应运算，运算结果再压回操作数栈）

例子1：

---

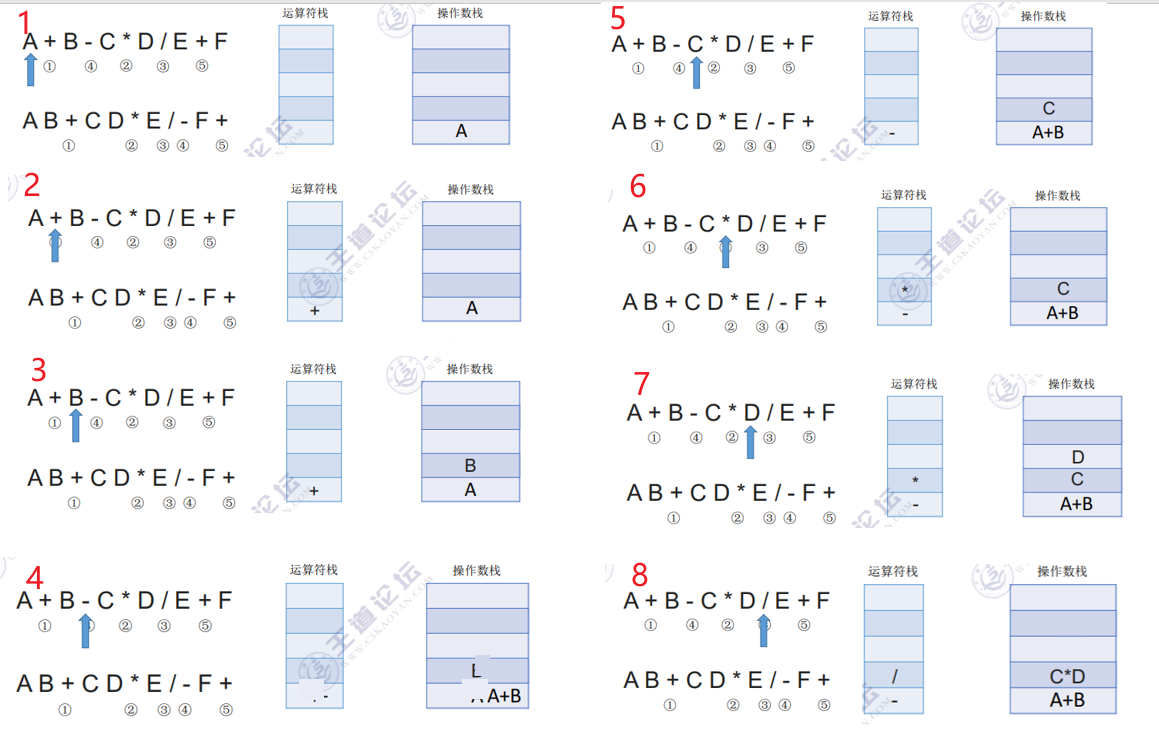
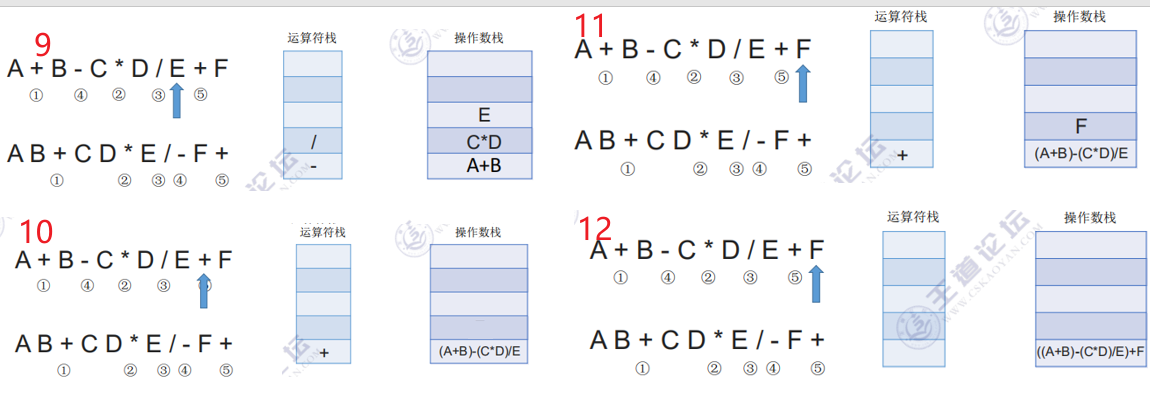
3. 中缀表达式转后缀表达式

3.1 【手算】实现中缀—>后缀

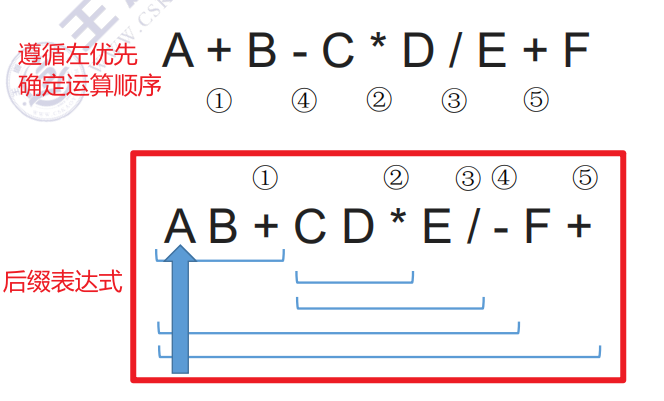
1. 遵循“左优先”原则：只要左边的运算符能先计算，就优先计算左边的，
   来确定中缀表达式中各个运算符的运算顺序。
2. 选择第一个运算符，按照【左操作数 右操作数 运算符】的方式组合成一个新的操作数。
3. 如果还有运算符没被处理，就继续执行步骤2。

例子1：A + B - C * D / E + F
 
1.左优先确定运算符的运算顺序

2.从①开始，选择两个操作数，依次类推

---

3.2 【用栈】实现中缀—>后缀

思路：

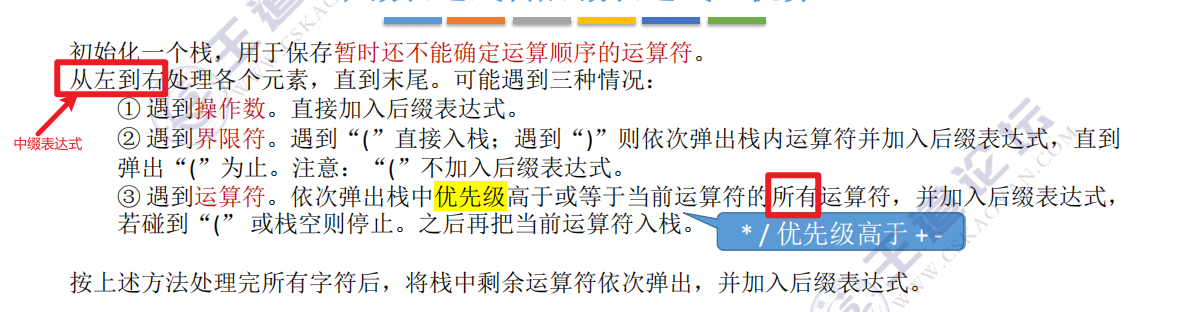
例子1：

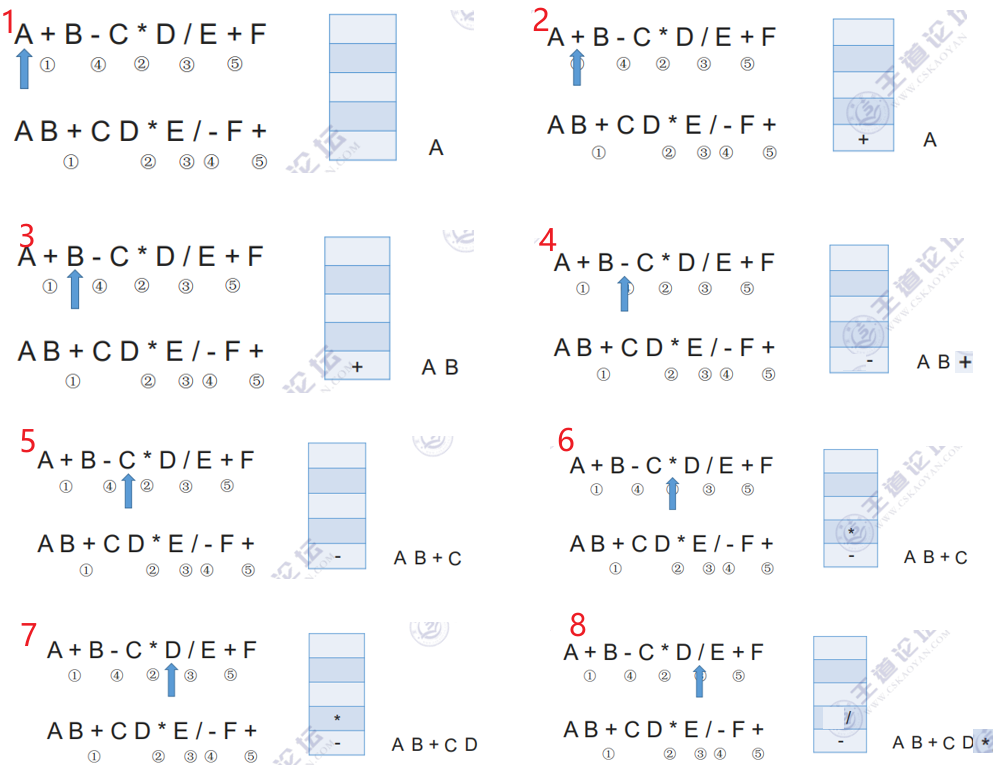
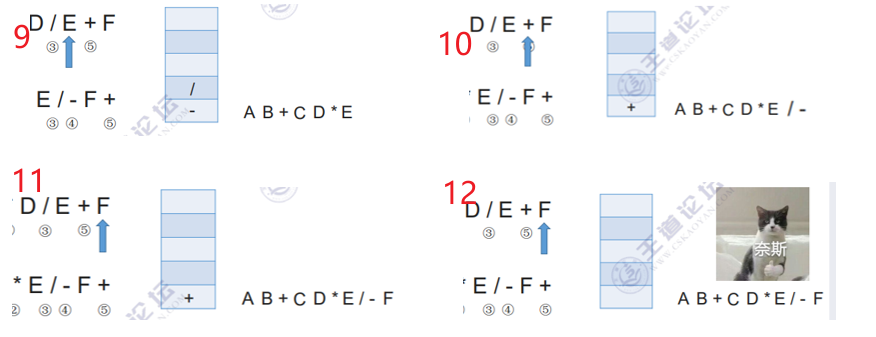
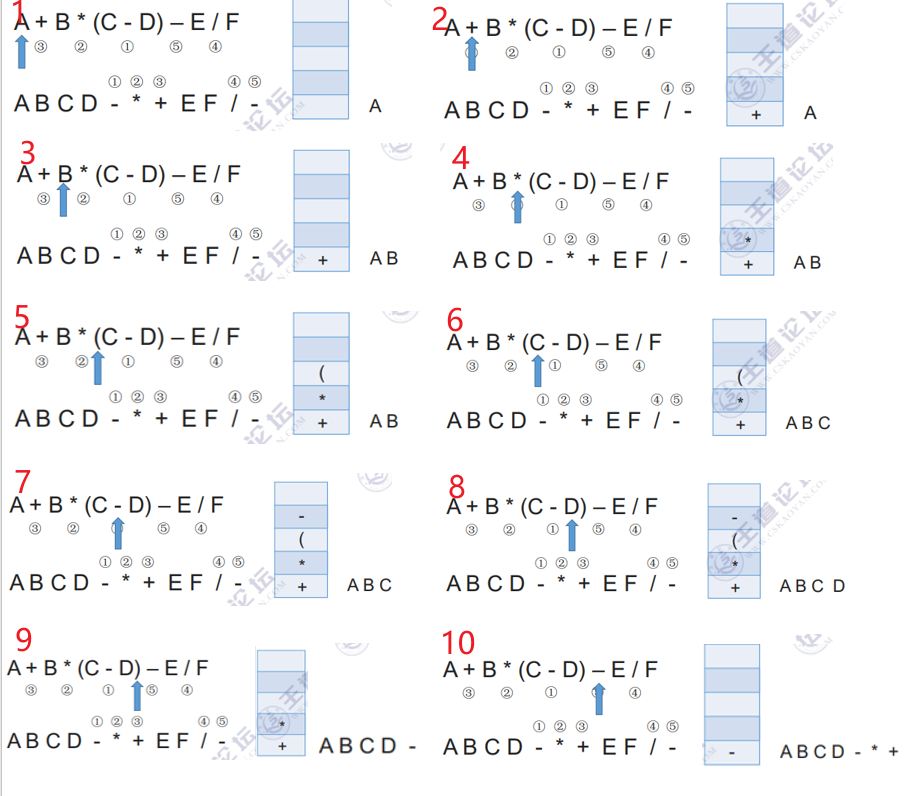
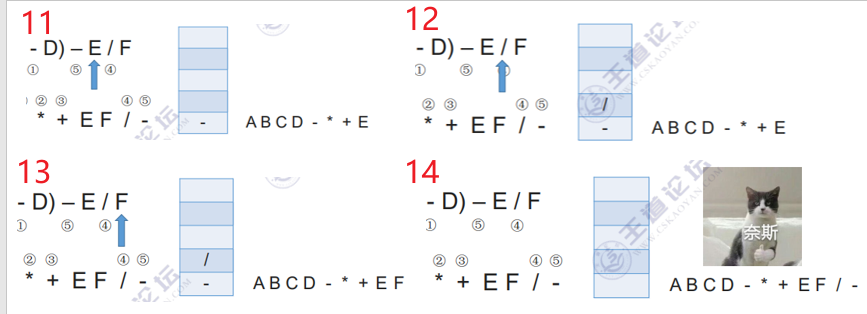
例子2

 

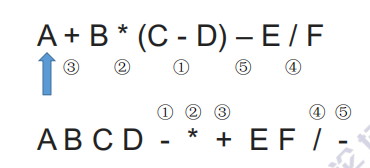
#define MaxSize 40 
typedef struct{     
    char data[MaxSize];   
    int top;
}SqStack;

typedef struct{  
    char data[MaxSize];  
    int front,rear;
}SqQueue;

void InitStack(SqStack &S);
bool StackEmpty(SqStack S);
bool Push(SqStack &S, char x);
bool Pop(SqStack &S, char &x);
void InitQueue(SqQueue &Q);
bool EnQueue(LQueue &Q, char x);
bool DeQueue(LQueue &Q, char &x);
bool QueueEmpty(SqQueue Q);

// 判断元素ch是否入栈
int JudgeEnStack(SqStack &S, char ch){
    char tp = S.data[S->top];   
    // 如果ch是a~z则返回-1    
    if(ch >= 'a' && ch <= 'z')   
        return -1;    
    // 如果ch是+、-、*、/且栈顶元素优先级大于等于ch则返回0  
    else if(ch == '+' && (tp == '+' || tp == '-' || tp == '*' || tp == '/'))   
        return 0;     
    else if(ch == '-' && (tp == '+' || tp == '-' || tp == '*' || tp == '/'))   
        return 0;  
    else if(ch == '*' && (tp == '*' || tp == '/'))  
        return 0;    
    else if(ch == '/' && (tp == '*' || tp == '/'))     
        return 0;    
    // 如果ch是右括号则返回2   
    else if(ch == ')')      
        return 2;     
    // 其他情况ch入栈，返回1   
    else return 1;
}

// 中缀表达式转后缀表达式
int main(int argc, char const *argv[]) {  
    SqStack S;     
    SqQueue Q;	 
    InitStack(S); 
    InitQueue(Q);  
    char ch;	  
    printf("请输入表达式，以“#”结束：");  
    scanf("%c", &ch);   
    while (ch != '#'){  
        // 当栈为空时     
        if(StackEmpty(&S)){ 
            // 如果输入的是数即a~z，直接入队 
            if(ch >= 'a' && ch <= 'z')               
                EnQueue(Q, ch);      	
            // 如果输入的是运算符，直接入栈    
            else                      
                Puch(S, ch);       
        }else{                
            // 当栈非空时，判断ch是否需要入栈 
            int n = JudgeEnStack(S, ch);     
            // 当输入是数字时直接入队      	
            if(n == -1){        	    
                EnQueue(Q, ch);        
            }else if(n == 0){       
                // 当输入是运算符且运算符优先级不高于栈顶元素时    
                while (1){         
                    // 取栈顶元素入队    
                    char tp;        
                    Pop(S, tp);      
                    EnQueue(Q, tp);         
                    // 再次判断是否需要入栈     
                    n = JudgeEnStack(S, ch);
                    // 当栈头优先级低于输入运算符或者栈头为‘)’时，入栈并跳出循环  
                    if(n != 0){           
                        EnStack(S, ch);           
                        break;              
                    }                   
                }            
            }else if(n == 2){  
                // 当出现‘)’时 将()中间的运算符全部出栈入队   
                while(1){                
                    char tp;                
                    Pop(S, tp);             
                    if(tp == '(')          
                        break;        
                    else            
                        EnQueue(Q, tp);    
                }             
            }else{        
                // 当运算符优先级高于栈顶元素或出现‘(’时直接入栈     
                Push(S, ch);         
            }          
        }         
        scanf("%c", &ch);   
    }     
    // 将最后栈中剩余的运算符出栈入队 
    while (!StackEmpty(S)){	  
        char tp;            
        Pop(S, tp);      
        EnQueue(Q, tp);  
    }      
    // 输出队中元素 
    while (!QueueEmpety(Q)){    
        printf("%c ", DeQueue(Q));  
    }    
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111

---

4. 中缀表达式转前缀表达式

4.1 【手算】实现中缀—>前缀

1. 遵循“右优先”原则：只要右边的运算符能先计算，就优先计算右边的，
   来确定中缀表达式中各个运算符的运算顺序。
2. 选择第一个运算符，按照【运算符 左操作数 右操作数 】的方式组合成一个新的操作数。
3. 如果还有运算符没被处理，就继续执行步骤2。

例子1：

4.2 【用栈】实现中缀—>前缀

参考本博客： 3.2 【用栈】实现中缀—>后缀
只是方向变了