图文并茂的—— 二叉树(附有源码实现)

---

每博一文案

世事浮沉，有太多的责任需要我们担当。生活中总有些挫折和磨难，让我们觉得快要扛不住了。
但当我们咬牙坚持过，那段难熬的时光后，发现并没有想象中的那么难。
就像岛上书店中的一句话，每个人的生命中都有最艰难的那一年，等你迈过去了，
人生就会变得高远辽阔，生活总是泥沙俱下，每个看似百毒不侵的成年人，都有
过无数次绝望和崩溃的时刻，要走的路已经选定了，该怎么走，走多久，
都是命中注定的，走多久都是命中注定。在一切变好之前，我们总要经历一段
不开心的日子。这段日子也许很长，也许只是一觉醒来，人只有不断地经历跌倒
才能顽强与坚毅的性格。
                                 ————————   一禅心灵庙语
1
2
3
4
5
6
7
8
9

---

---

创建项目的注意事项

• 首先我们要明白一点就是不存在没有完完全全BUG的项目，就像人无完人一样 我们只能不断地对项目进行优化，减少BUG 的出现，但是我们好像并不能完全的消除所有的BUG
• 而消除bug 的最好的方式就是运行测试+调试
• 而我们在运行测试+调试 的时候，需要我们控制一定的量 ，我们需要把握住这个量 ，这一点是十分重要的，这样有助于我们快速的发现问题，也就是bug 的所在，从而提高我们的效率，减少我们的bug 的出现
• 具体的方法，我个人有以下建议：

1. 首先我们需要对项目进行合理的分类，那个类，那个文件实现什么样的功能： 比如:一个类是用于定义什么类型，方法的 ，另一个类是用于什么头main 的，再另外一个类是用于对于什么功能上的实现的 ，合理的分类，可以提高我们项目的可读性，让我们自身不会因为自己随着代码量的增加，对应功能上的增加而导致我们越敲越乱，越写越蒙
2. 对于量上我们可以，每实现了两三个 功能就运行测试看看，是否存在错误，如果存在出现了错误，我们可以在一定的量(范围内)，快速的找出哪里出现了问题，从而对它进行调试 ，解决问题，而不是，把项目整体写完了或者是已经实现了好几十个功能，才开始运行测试项目，结果一运行，bug,警告 冒出一大坨，我们先不说，让不让人，抓头发，就是找出问题，恐怕都需要不时间上的浪费吧
3. 对于代码上的注释，没事多写明白一点，或许有一天，你会感想曾经，那个写了注释的自己或同事
4. 对于bug 不要害怕，一点一点的调试看看，找出问题的所在，慢慢来，要有耐心，要明白一点现在bug 写的多，以后bug 跟你说拜拜，现在bug ,不解决，bug 天天对你说 明天见

---

树的概念

在实现生活中，存在很多的一对多 的情况需要处理，所以我们需要研究这种一对多的数据结构 —— “树” ，

树: 是一种非线性的数据结构，它是由 n (N >= 0 ) 个有限的节点组成的一个具有层次关系的集合，把它叫做树，是因为它看起来像一个倒挂的树，也就是说它是根朝上，而叶朝下的。

树的一些特点

• 树，有且仅有一个特殊的节点，没有前驱(没有父节点)，称为 根节点
• 除根节点以外，其余节点被分成为 M(M > 0) 个互不相交的集合 ，T1,T2… ,Tn , 其中的每个集合 Ti (1 <= i < =m ) 又是一棵结构与树类似的子树，因此树的定义其实就是我们递归的方法，也就是在树的定义之中还 用到了树的概念，这是一种比较新的定义方法，说简单点就是，把每个节点都看成是棵树的结构定义
• 每个子树的节点只有一个前驱，可以有 0 个 或多个后继(子树)
• 每个子树之间不可以相交

---

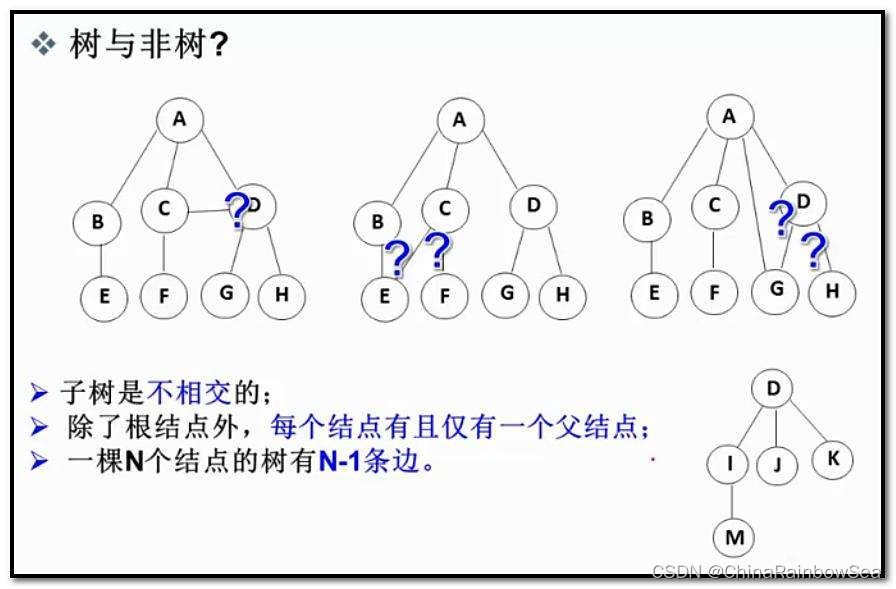
树的表示

树的结构相对线性表而言是比较复杂的，要存储表示起来也比较麻烦，在实际中树的有许多种表示的方式：如：双亲表示法，孩子表示法，孩子兄弟表示法等等 ，这里我们只简单介绍一种 孩子兄弟表示法

所谓的孩子兄弟表示法 ，其实就是创建一个结构体，存放一颗树中的 左孩子的地址，和其兄弟的地址的指针，从而建立树与子树的联系关系。

// 孩子兄弟表示法
typedef char BTDataType;

typedef struct Node
{
	struct Node* firstChild;       // 指向左孩子的节点的指针
	struct Node* pNextBrother;     // 指向其兄弟节点的指针
	BTDataType data;               // 树节点存放的数据
}Node;
1
2
3
4
5
6
7
8
9

树的实际运用主要是在 文件系统中的目录 ，因为使用树结构可以，明显的表示出每个目录中的文件的路径位置是绝对的 ，不存在重复的路径

---

二叉树的结构概念

二叉树 ：是 (n > = 0 ) 个节点的有限集合，该集合可以 0 ，为空集合(空二叉树)，或者由一个根节点和两棵互不相交 的，分别称为根的左子树 和右子树 的二叉树组合成的

二叉树的特点

• 每个节点最多有两棵子树，所以二叉树中不存在度 > 2 的节点。注意: 不是只有两棵子树，而是最多有，没有子树或者有一棵子树都是可以的。
• 左子树和右子树是有顺序的，次序不能任意颠倒。就像人有双手，双脚，但是显然左手，左脚和右手，右脚是不一样的，右手戴左手套，右脚穿左鞋都会极其变扭和难受。
• 即使二叉树种只有一棵子树，也要区分它是左子树还是右子树，下图中，树1和树2是同一棵树，但它们却是不同的二叉树，就好像你一不小心，摔伤了手，伤的是左手还是右手，对你的生活影响是完全不同的

---

特殊的二叉树

满二叉树 ： 在一棵二叉树中，如果所有分支中的节点都存在左子树和右子树，并且所有的叶子都在同一层上，这样的二叉树称为 满二叉树 。注意 ： 单是每个节点都存在左子树和右子树，并不能认定是 满二叉树，还必须要所有的叶子节点都是在同一层上，这就做到了整棵树的平衡，才为 满二叉树。

完全二叉树 ：是效率很高的数据结构，完全二叉树是由满二叉树，引出来的，对于深度 为 K 的，有 n 个节点的二叉树，当且仅当其每个节点都与深度 为 K 的满二叉树中的编号，从 1 至 n 的节点—— 对应时，称为完全二叉树。说白了就是，完全二叉树是 所有的叶子节点在最后一层，并且所有的叶子节点是连续紧挨着的，不可以分开。满二叉树是完全二叉树中的特殊情况，就是完全二叉树中的所有节点都满了

注意： 满二叉树一定是完全二叉树，而完全二叉树不一定是满二叉树

---

二叉树链表的形式的结构

二叉树的链式存储结构 用链表来表示一棵二叉树，即用链来指示数据之间的逻辑关系。通常的方法是链表中每个节点由三个域组成，数据域和左右指针域，左右指针分别用来给出，该节点的左孩子和右孩子所在的链节点的存储地址。链式结构又分为 二叉链 和 三叉链 ，当前我们学习中一般都是二叉链表，而一般高级数据结构如，红黑树，会用到三叉树

typedef char BTDataType;
// 二叉链
typedef struct BinaryTwoNode
{
	struct BinaryTwoNode* pLeft;    // 指向当前左孩子的节点的指针
	struct BinaryTwoNode* pRight;   // 指向当前右孩子的节点的指针
	BTDataType data;                 // 存放的二叉树中的节点的数据
}BTwoNode;
1
2
3
4
5
6
7
8

---

typedef char BTDataType;
// 三叉链
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* pParent;  // 指向当前双亲节点的指针
	struct BinaryTreeNode* pLeft;    // 指向当前左孩子的指针
	struct BinaryTreeNode* pRight;   // 指向当前右孩子的指针
	BTDataType data;                 // 当前二叉树节点存放的数据
}BTreeNode;
1
2
3
4
5
6
7
8
9

---

二叉树链表的代码实现

这里我们使用链表实现二叉树的

创建二叉树的结构体

通过链表实现二叉树，一个数据域，两个指针域

typedef char BTDataType;

// 二叉树的结构体
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;    // 当前节点的左子树
	struct BinaryTreeNode* right;   // 当前节点的右子树
	BTDataType data;                // 当前节点的存放的数据
}BTNode; 

1
2
3
4
5
6
7
8
9
10

---

生成二叉树节点

传存放的数据，通过 malloc 函数动态开辟内存(堆区上)，生成二叉树节点,

注意 ： 一定要判断动态开辟的空间是否，真正开辟成功了，如果失败了，又使用该空间，的话，会报错的，所以一定要再使用前，进行判断，确保开辟成功。再使用，失败了，给予代码提示，容易定位错误，提高代码的健壮性。

// 生成二叉树节点
BTNode* BiTreeCreate(BTDataType x)
{
	// malloc 堆区上开辟空间
	BTNode* new = (BTNode*)malloc(sizeof(BTNode));
	
	// 判断动态开辟空间是否，成功
	if (NULL == new)  
	{
		perror("malloc error");    // 堆区内存开辟空间，失败，错误提示
		exit(-1);                  // 同时，非正常退出，程序
	}
	else                           // 开辟空间成功
	{
		new->data = x;             // 数据存入到，当前节点的数据域中
		new->left = NULL;
		new->right = NULL;
	}

	return new;          // 返回堆区上开辟的空间的地址指针
} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

---

建立二叉树节点关系

我们根据如下的二叉树，为每个二叉树节点之间建立相关的联系

---

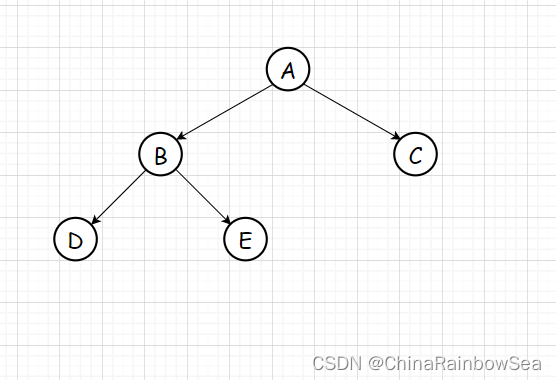
int main()
{
	// 生成二叉树节点
	BTNode* A = BiTreeCreate('A');
	BTNode* B = BiTreeCreate('B');
	BTNode* C = BiTreeCreate('C');
	BTNode* D = BiTreeCreate('D');
	BTNode* E = BiTreeCreate('E');

	// 构建二叉树联系
	A->left = B; 
	A->right = C;
	B->left = D;
	B->right = E;

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

---

二叉树的前序遍历

前序遍历又被称为是先根遍历，规则是若二叉树为空，则空操作返回，否则先访问根节点——>再前序遍历当前节点的左子树——> 最后再前序遍历访问当前节点的右子树。

总结一点就是，把每个节点都当成是一个树 包含（ 根节点 左子树，右子树） [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传
，这样我们就可以使用，分治算法，分而治之，大问题分成类似的子问题，子问题，再分成子问题，直到子问题不可再分割，了。这种方式的处理，运用递归，如下图中的二叉树：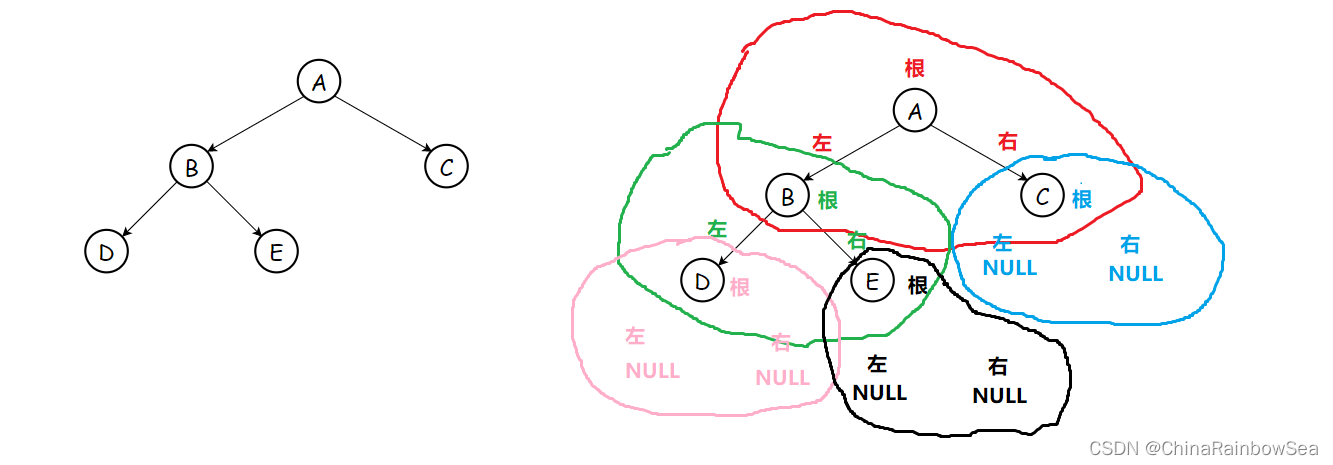

根据如上二叉树其 前序遍历结果 ：A B D NULL NULL E NULL NULL C NULL NULL

// 前序遍历
void PrevOrder(BTNode* root)
{
	if (NULL == root)     // 递归结束条件
	{
		printf("NULL ");
		return;           // 返回调用该函数的位置
	}
	else
	{
		printf("%c ", root->data);     // 访问当前的根节点
		PrevOrder(root->left);         // 递归，访问当前的节点的左子树
		PrevOrder(root->right);        // 递归，访问当前的节点的右子树
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

运行结果

---

前序遍历递归结构展开图

---

二叉树的中序遍历

中序遍历又称为中根遍历，规则是若树为空，则空操作返回，否则 不为空，中序遍历当前根节点的左子树——> 然后再访问中序遍历当前的根节点——> 最后中序遍历当前节点的右子树。同样把每个节点看作是 （根，左，右） [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传
，来递归访问，左子树——> 根——> 右子树

上述二叉树的中序遍历结果 ： NULL D NULL B NULL E NULL A NULL C NULL

// 中序遍历
void InOrder(BTNode* root)
{
	if (NULL == root)    // 递归结束条件
	{
		printf("NULL ");
		return;          // 返回，调用该函数的位置
	}
	else
	{
		InOrder(root->left);          // 递归，当前节点的左子树
		printf("%c ", root->data);     // 打印当前节点的数据
		InOrder(root->right);         // 递归，当前节点的右子树
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

运行结果

---

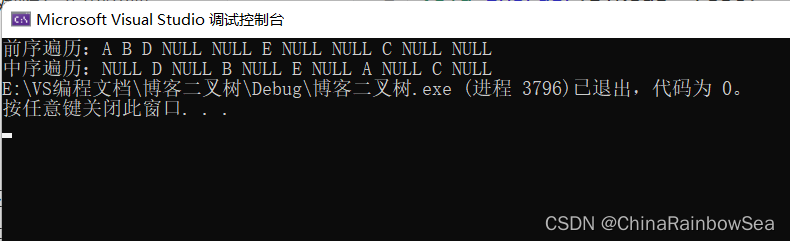
中序遍历递归结构展开图

---

二叉树的后序遍历

后序遍历又称为后根遍历，规则是若树为空，则空操作返回，否则不为空，先后序遍历当前节点的左子树——> 然后后序遍历当前节点的右子树——> 最后后序遍历当前节点的根节点；同样把每个节点看作是 （根，左，右）的[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传
形式理解，递归

上述二叉树的后序遍历结果： NULL NULL D NULL NULL E B NULL NULL C A

// 后序遍历
void PostOrder(BTNode* root)
{
	if (NULL == root)  // 递归结束条件
	{
		printf("NULL ");
		return;
	}
	else
	{
		PostOrder(root->left);   // 递归左子树
		PostOrder(root->right);  // 递归右子树
		printf("%c ", root->data);  // 打印当前的节点存放的数据
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

运行结果

---

后序遍历递归的展开图

---

二叉树的层序遍历

层序遍历 ：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的 根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然 后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问 树的结点的过程就是层序遍历。就是从根节点开始一层一层的从左向右的的访问下去;

这里我们使用队列的方式，进行层序遍历：把根节点入队列，同时定义出队该根节点，拷贝复制一下，循环把该节点的左子树和右子树的也就是下一层节点的数据入队列，

所以需要创建一个队列用于存放

核心思想就是 一层节点的出队带入下一层节点入队列

---

// 层序遍历
/* 核心思想就是，节点不为空入队，再出队，
* 一层中带下一层的数据节点
*/
void LeveIOrder(BTNode* root)
{
	Queue q;  // 定义队列
	QueueInit(&q);   // 初始化队列

	if (root)
	{
		QueuePush(&q, root);   // 根节点入队
	}

	while (!QueueEmpty(&q))      // 当队列为空时，表示二叉树，层序遍历完了
	{
		BTNode* front = QueueFront(&q);   // 取出队列中存放的 根节点
		QueuePop(&q);                    // 出队 ，是一起的，不然无法取到后面的数据
		printf("%c ", front->data);

		if (front->left)
		{
			QueuePush(&q, front->left);    // 当前节点的左子树不为空，入队列
		}
		else
		{
			printf("NULL ");
		}

		if (front->right)
		{
			QueuePush(&q, front->right);    // 当前节点的，右子树不为空，入队列
		}
		else
		{
			printf("NULL ");
		}
	
	}

	printf("\n");
	QueueDestory(&q);   // 清空队列
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

---

清空二叉树中的节点

注意：我们在清空二叉树中的节点的时候，不要 先把根节点中的数据给清除了，如果删除了，就无法访问后面的数据了。所以我们，先后序遍历一样，把根放到最后，释放空间，这里我们同样使用递归的方式把每个节点看成是（根，左子树，右子树），释放空间

// 清空二叉树中的节点
/*
*  注意：在二叉树中的不要把根节点，删除了，不然，无法找到左右子树
*        所以我们需要从最后面，删除，后序遍历类似
*/
void DestroryTree(BTNode* root)
{
	if (NULL == root)
	{
		return;
	}

	DestroryTree(root->left);      // 清空当前节点的左子树
	DestroryTree(root->right);     // 清空当前节点的右子树

	free(root);                    // 释放当前节点的空间

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

---

计算二叉树中所有节点的个数

计算二叉树中所有的节点的个数，我们这里有三种方式：

第一种方式，定义全局变量 递归计算:

定义全局变量的原因是：

如果没有定义全局变量的话，像下面这种 int size = 0 没有被定义全局变量，而是定义成了局部变量，出现的问题就是在，递归的过程中，对被不断初始化为 0 ，导致无法计数到

// 计算二叉树中所有节点的个数 
// 方式一: 定义全局变量，递归计数
int size = 0;
void TreeSizeOne(BTNode* root)
{
	int size = 0;    // 注意这里，每次递归的时候都会被，初始化为 0 ，是没有办法计数到的
	 
	if (NULL == root)   // 节点为空不计数
	{
		return;
	}
	else
	{
		++size;   //递归计数
	}

	TreeSizeOne(root->left);    // 左子树中的所有节点个数
	TreeSizeOne(root->right);   // 右子树中的所有节点个数

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

运行结果

---

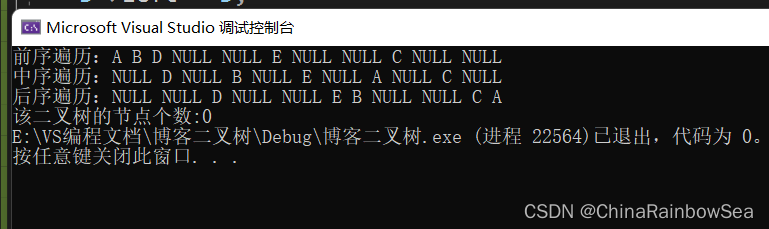
修改一下我们定义一个全局变量，进行计数，代码如下：

int size = 0;
void TreeSizeOne(BTNode* root)
{
	 
	if (NULL == root)   // 节点为空不计数
	{
		return;
	}
	else
	{
		++size;   //递归计数
	}

	TreeSizeOne(root->left);    // 左子树中的所有节点个数
	TreeSizeOne(root->right);   // 右子树中的所有节点个数

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

运行结果:

---

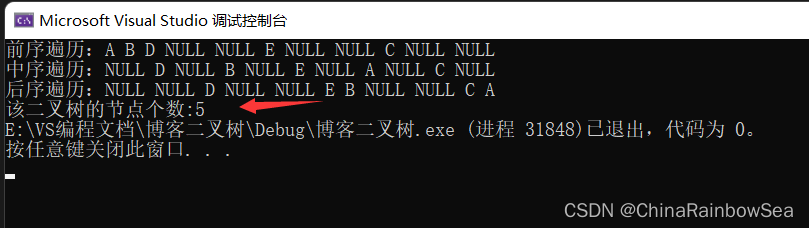
运行结果上看是没有问题的，但是，存在一个问题就是，因为我们定义的是全局变量，当我们计算另外一个二叉树的节点时，会把我们前面的计算的结果累加到一起，其结果就不正确了。

第二种方式: 传参数，递归计算

注意 ：需要传参数的地址，因为形参的改变并不会影响到实参

具体代码实现如下：

// 计算二叉树中所有节点的个数的 
// 方式2：传参数的地址，改变实参 递归计数
void TreeSizeTwo(BTNode* root,int* size)
{
	if (NULL == root)
	{
		return;
	}
	else
	{
		++(*size);     // 解引用改变实参
	}

	TreeSizeTwo(root->left,size);    // 递归，计算左子树的节点个数
	TreeSizeTwo(root->right,size);   // 递归，计算右子树的节点个数
	
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

第三种方式：运用递归返回计数

把每个节点看作是（根，左子树，右子树），进行递归计算其左右子树的节点，计算好后一一返回，计算总合

int TreeSize(BTNode* root)
{
	if (NULL == root)   // 空节点不用计数，返回 0 
	{
		return 0;
	}
	else
	{
		return TreeSize(root->left) + TreeSize(root->right) + 1; // +1 指的是当前不为空的，本身节点
		 //      递归计算左子树中的节点         右子树的节点
	}
}
1
2
3
4
5
6
7
8
9
10
11
12

---

计算二叉树中所有节点的递归展开图

---

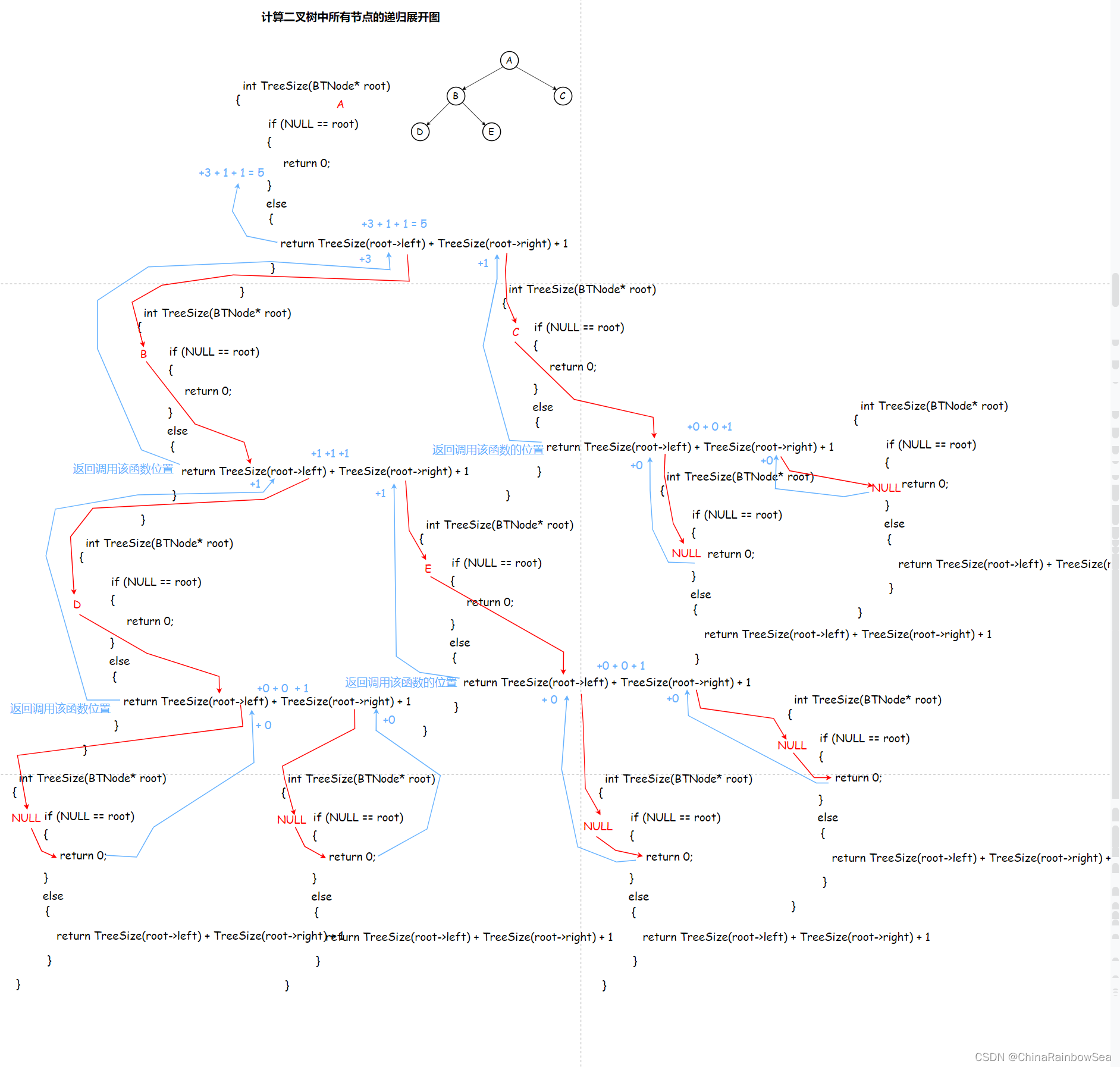
计算二叉树中所有叶子节点的个数

同样计算二叉树中所有叶子节点的个数，我们也可以使用递归分治算法 ，分而治之，将大问题，分成类似的小问题，使用同样的方法，解决。这里我们把每个节点的看作是（根，左子树，右子树） [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传
进行递归分治之，把每个节点中的左子树和右子树计算出来后，一一递归回溯返回，最后汇总计算总和

// 计算二叉树中所有叶子节点的个数
int TreeLeafSize(BTNode* root)
{
	if (root == NULL)    // 节点为空，返回 0
	{
		return 0;
	}
	
	if (NULL == root->left && NULL == root->right)    // 左右子树都为 NULL, 为叶子节点，返回 1 计数
	{
		return 1;
	}

	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
	//      计算 左子树               +   计算 右子树         的叶子节点
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

运行结果

---

计算二叉树中所有叶子节点的递归展开图

---

二叉树完整代码实现

这里使用分布式文件设计模式实现的

BinaryTree.h

该文件存放，头文件的引入，二叉树的结构体定义，有关二叉树函数的声明，宏定义

#pragma once
#define  _CRT_SECURE_NO_WARNINGS  1

#include
#include

typedef char BTDateType;    // 定义存放二叉树中的数据类型

typedef struct BinaryTreeNode {    // 定义二叉树结构体
	struct BinaryTreeNode* left;   // 左子树的
	struct BinaryTreeNode* right;  // 右子树
	BTDateType data;               // 存放的数据

}BTNode;


// extern int size1 ; 存在累计问题

extern void test();        // 用于测试二叉树
extern void BinaryTreeInit(BTNode* root);     // 初始化二叉树
extern BTNode* BinaryTreeGenerate(BTDateType x);   // 产生树节点
extern void PrerOrder(BTNode* root);   // 前序遍历
extern void InOrder(BTNode* root);     // 中序遍历
extern void PostOrder(BTNode* root);   // 后序遍历
// extern void TreeSize1(BTNode* root);              // 计算二叉树的节点个数,方式一：全局变量
// extern void TreeSize2(BTNode* root, int* size);   // 计算二叉树的节点的个数，方式二：传参数，注意时传的是地址
                                                     // 因为形参的改变不会影响到实参的，传地址
extern int TreeSize(BTNode* root);       // 计算二叉树中第三中方式，递归计算
extern int TreeLeafSize(BTNode* root);   // 计算二叉树中叶子节点的个数
extern void DestroryTree(BTNode* root);  // 清空二叉树中的节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

---

BinaryTree.c

该文件存放，有关二叉树功能的函数的实现

#include"BinaryTree.h"


// 初始化二叉树的
void BinaryTreeInit(BTNode* root)
{
	root->left = NULL; 
	root->right = NULL;
}



// 生成二叉树节点
BTNode* BinaryTreeGenerate(BTDateType x)
{
	// 内存堆区开辟空间
	BTNode* new = (BTNode*)malloc(sizeof(BTNode));
	// 判断该空间是否创建成功
	if (NULL == new)
	{
		perror("malloc error");   // 打印提示错误
		exit(-1);
	}

	new->left = NULL;     // 左子树节点
	new->right = NULL;    // 右子树节点
	new->data = x;        // 存放的数值

	return new;
}


//  前序遍历
// 将每个节点看作是 根左右，来递归
void PrerOrder(BTNode* root)
{
	if (NULL == root)     // 递归结束条件
	{
		printf("NULL ");
		return;           // 返回到调用它的位置
	}

	printf("%c ", root->data);  // 取根
	PrerOrder(root->left);      // 左子树递归，
	PrerOrder(root->right);     // 右子树递归

}



// 中序遍历
// 把每个节点看作是 根左右，进行递归
void InOrder(BTNode* root)
{
	if (NULL == root)    // 递归结束条件
	{
		printf("NULL ");
		return;          // 递归，返回到调用该函数的位置
	}

	InOrder(root->left);        // 左子树，递归
	printf("%c ", root->data);  // 取根
	InOrder(root->right);       // 右子树，递归

}


// 后序遍历
// 将每个节点看作是 根左右
void PostOrder(BTNode* root)
{
	if (NULL == root)   // 递归结束条件
	{
		printf("NULL ");
		return;         // 递归，返回调用它的位置处
	}
	else
	{
		PostOrder(root->left);      // 左子树递归
		PostOrder(root->right);     // 右子树，递归
		printf("%c ", root->data);  // 取 根
		
	}
}



// 计算二叉树中所有节点的个数，方式三
/* 递归，计算，把每个节点看作是 根左右，计算每个节点的数量*/
int TreeSize(BTNode* root)
{
	if (NULL == root)  // 递归结束条件
	{
		return 0;      // 当左右树节点为 NULL,返回 0，返回调用它的位置
	}
	else
	{
		return TreeSize(root->left) + TreeSize(root->right) + 1;
		// 把其节点的左右子树的节点个数加起来
	}

}



// 计算二叉树中叶子节点的个数 注意把每个节点看成是 根左右的树
int TreeLeafSize(BTNode* root)
{
	if (NULL == root)   // 递归结束条件
	{
		return 0;       // 空节点 0，返回调用它的位置
	}
	
	if (root->left == NULL && root->right == NULL)
	{
		return 1;  // 左右子树都为空，返回 1， 返回到调用它的位置
	}

	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
	       // 子树的叶子节点          +   右子树的叶子节点
}




// 清空二叉树中的节点
/*
*  注意：在二叉树中的不要把根节点，删除了，不然，无法找到左右子树
*        所以我们需要从最后面，删除，后序遍历类似
*/
void DestroryTree(BTNode* root)
{
	if (NULL == root)
	{
		return;
	}

	DestroryTree(root->left);      // 清空当前节点的左子树
	DestroryTree(root->right);     // 清空当前节点的右子树

	free(root);                    // 释放当前节点的空间

}



// 计算二叉树的节点的个数 ，把每个节点看作是 根左右
/* 方式二，传参数的地址的方式，改变形参影响实参
void TreeSize2(BTNode* root, int* size)
{
	if (NULL == root)  // 递归结束条件
	{
		return;  // 返回，调用你的位置处；
	}
	else    
	{
		(*size)++;  // 解引用，形参改变实参
	}

	TreeSize2(root->left, size);  // 递归,左子树
	TreeSize2(root->right, size); // 递归，右子树


}
*/



/*
void TreeSize2(BTNode* root)
{
	int size = 0;   // 该计算的数值，会在递归中，被不断置为 0，导致无法计数
	if (NULL == root)  // 所以使用传参数的地址的方式
	{
		return;
	}
	else
	{
		size++;
	}

	TreeSize2(root->left);
	TreeSize2(root->right);

}
*/


// 计算二叉树的节点个数
/*方式一，定义全局变量,累计计算
* 存在累计问题
void TreeSize1(BTNode* root)
{

	if (NULL == root)     // 递归结束条件
	{
		return ;
	}
	else
	{
		size1++;    // 节点不为空加加
	}

	TreeSize1(root->left);   // 递归，计算其左子树
	TreeSize1(root->right);  // 递归，计算其右子树

	return ;
}
*/




1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214

---

Test.c

该文件存放 main函数 ，有关二叉树中的测试

#include"BinaryTree.h"

// int size1 = 0;   // 计算二叉树节点的方式一，全局变量，存在累计问题
int main()
{
	test();

	return 0;
}


void test()
{
	BTNode* A = NULL;
	BTNode* B = NULL;
	BTNode* C = NULL;
	BTNode* D = NULL;
	BTNode* E = NULL;


	A = BinaryTreeGenerate('A');  // 创建生成二叉树节点
	B = BinaryTreeGenerate('B');
	C = BinaryTreeGenerate('C');
	D = BinaryTreeGenerate('D');
	E = BinaryTreeGenerate('E');

	A->left = B;      // A的左子树
	A->right = C;     // A的右子树
	B->left = D;      // B的左子树
	B->right = E;     // B的右子树

	printf("前序遍历: ");
	PrerOrder(A);     // 前序遍历
	printf("\n");   
	printf("中序遍历: ");
	InOrder(A);       // 中序遍历
	printf("\n");
	printf("后序遍历: ");
	PostOrder(A);     // 后序遍历

	/*
	* 使用方式一：定义全局变量，计算二叉树节点存在累积问题
	TreeSize1(A);
	printf("\n");
	printf("%d\n", size1); // 5
	TreeSize1(B); 
	printf("%d\n", size1); // 8 这里size 累计到了上次的size的数值了
	*/

	/*使用方式二：传实参的地址，形参的改变影响实参
	int size = 0;
	printf("\n");
	TreeSize2(A, &size);
	printf("%d\n", size);
	int num = 0;
	TreeSize2(B, &num);
	printf("%d\n", num);
	*/

	printf("\n以A为根节点的二叉树中的所有节点的个数：%d",TreeSize(A));    // 计算二叉树中所有节点的个数
	printf("\n以B为根节点的二叉树中的所有节点的个数：%d\n",TreeSize(B));    // 计算二叉树中所有节点的个数
	printf("以A为根节点的二叉树中的所有叶子节点个数：%d", TreeLeafSize(A));   // 计算二叉树中所有叶子节点的个数
	printf("\n");
	printf("以B为根节点的二叉树中的所有叶子节点个数：%d", TreeLeafSize(B));   // 计算二叉树中所有叶子节点的个数
	printf("\n");
	printf("以C为根节点的二叉树中的所有叶子节点个数：%d", TreeLeafSize(C));   // 计算二叉树中所有叶子节点的个数


	DestroryTree(A);      // 清空二叉树中的节点

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

---

运行结果

---

最后:

限于自身水平，其中存在的错误，希望大家给予指教，韩信点兵——多多益善，谢谢大家，后会有期，江湖再见

---