Decoupled Contrastive Learning 论文解读和感想

本文首先提出了当前对比学习的三大痛点：
1、当前的sota方法结构都过于复杂
2、对比学习要想取得效果，必须要用大batch
3、超参敏感(个人认为这里说的超参是指数据增强方式)
然后本文以SimCLR为例，通过对对比损失的梯度进行分析，发现了导致上面2、3的原因，并且在不改变网络结果的前提下提出了一种超简洁的优化方式。

先来看SimCLR的损失，对于第i个训练样本，其loss为：

其中

那么其第一个增强view的梯度为

其中

由于对称性，可以很容易的推出其第二个view的梯度。
我们对$q_{B,i}^{(1)}$进行分析，可以看出其值属于$(0,1)$，并且：
1、当负样本相距太远时(称之为easy negative)，此时分母$U_{i,k}$会变得很小，由此被减项会趋向于1，即$q_{B,i}^{(1)}$趋向于0
2、当正样本相距太近时(称之为easy positive)，此时将上式变形为

可以看出整体依然趋向于0
3、当batch太小时，可以看成是无监督分类(对正负样本的二分类)任务变得过于简单，作为结果，会导致上面两张情况同时发生。
为了验证分析，作者也给出了相应的图例：

可以看出，当batch变太小时不仅$q_B$的分布会趋向于0，并且其协方差也会变大，反映在模型上就是训练会变得极不稳定。
因此，想要避免这三种情况对训练的影响，可以转化成避免$q_{B,i}^{(1)}$对梯度的影响。那么一个直接的方式就是将其直接改写成1(相当于batch→无穷的效果)。通过公式反推，作者惊奇的发现去掉$q_B$就相当于在loss中去掉分母的第一项，因此作者提出将对比损失改写成下面形式：

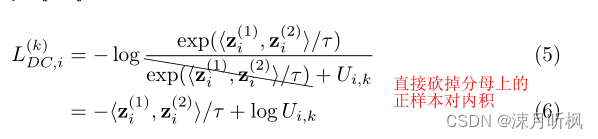
此外为了平衡去掉这一项带来的正样本难易程度自适应问题，作者添加了一项新的权重项：

其中$\sigma$类似于温度系数，当$\sigma$→无穷时，权重项恒等于1。最终loss为：

实验部分的话，作者虽然做了很多实验，但是归结起来就是一点，本文的对比loss要优于传统的对比loss，并且batch越小提升幅度越大：