手写哈希表

​
​

活动地址：CSDN21天学习挑战赛

前言

对哈希表，平常做题用的很多的是容器：map，unordered_map，对于这两个容器呢，我有详细的介绍在c++知识专栏

简单介绍

散列表（Hash table，也叫哈希表），是根据关键码值(Key value)而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。
给定表M，存在函数f(key)，对任意给定的关键字值key，代入函数后若能得到包含该关键字的记录在表中的地址，则称表M为哈希（Hash）表，函数f(key)为哈希(Hash) 函数。

模拟散列表（例题）

点击跳转至例题 模拟散列表
这道题要求要求维护一个集合，支持以下操作：

1. 插入一个数x
2. 询问数x是否在集合中出现过

注意：对于哈希表的下标范围，需要是一个质数，这道题数据范围是1e5，最小的质数是100003 ，但是一般可以设置为 199997

• x % N 如果x为负数的话，那么结果就会是负数，但是h数组是没有负数下标的，为了解决这个问题，我们可以进行这个操作 (x % N + N) % N
• memset 的头文件是 cstring

#include
#include
using namespace std ;
const int N = 199997 , inf = 0x3f3f3f3f;
int h[N];
int find(int x)
{
    int t = (x % N + N) % N ;
    while(h[t] != inf && h[t] != x)
    {
        if( ++ t == N) t = 0 ;
    }
    return t;
}
int main()
{
    int T ;
    cin >> T;
    memset(h , 0x3f , sizeof h);
    while(T--)
    {
        char s[2];
        cin >> s[0];
        if(*s == 'I')
        {
            int x ;
            cin >> x ;
            h[find(x)] = x ;
        }
        else 
        {
            int x ;
            cin >> x ;
            if(h[find(x)] == inf) cout << "No" <<endl;
            else cout << "Yes" << endl; 
        }
    }
    return 0 ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

最大子集（acwing63场周赛）

​点击跳转至周赛题：最大子集
在题目中，说容器慎用，所以用容器大概率是不好过的，重点：证明最大子集中的长度最大为3

这里的证明方法是acwing创始人 y总的证明方法，我直接搬过来了。

证明：
假设 a < b < c < d , {a,b,c,d}是满足题意的一个子集，所以有图可见

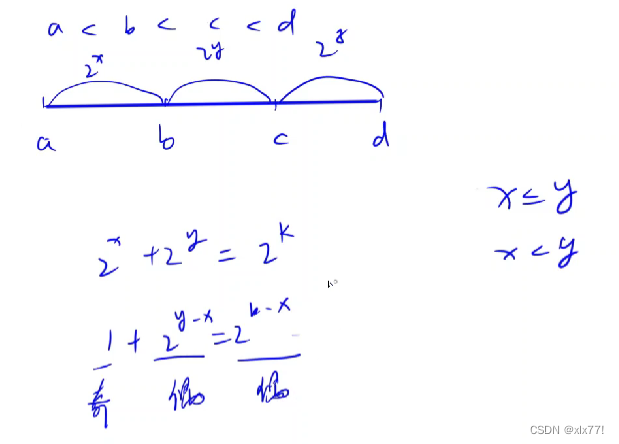
左右同时除以 2的x次方，得到最下面的式子： 左边为1（奇数）和2的y-x次方（偶数），右边是2的k-x次方（偶数）。奇数加偶数不可能是偶数，除非2的y-x次方为奇数，即 y==x

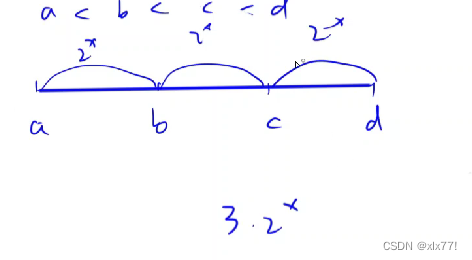
然后我们可以发现在 a 和 d之间的差值是3*2的x次方，显然不是2的整数次幂，所以这道题符合题意的最大长度为3

算法复杂度：

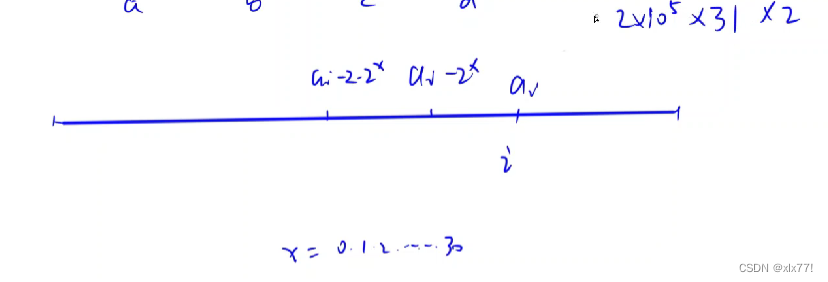
遍历每一个数，看它前两个数是否满足题意凑成子集

• 若第一个数满足，第二个数不满足就在结构数组里加入第一个，而不加入第二个
• 若两个都满足，那么直接跳出循环进行输出
• 若都不满足，那就是第一个数，因为一直没有更新答案

这里的31，是因为题目上数据范围是-10的9次方~10的九次方，那么最极限的减法结果是 2e9 ， 大于2e9的最小的2的整数幂是2的31次幂
一个结果，一个中间数组：

• 因为是从后往前找是否满足的数，所以先把找到的符合题意的数放入中间数组，然后如果 结果数组中的元素数目小于中间数组时，就更新结果数组

#include
#include
#include
using namespace std ;
const int N = 1999997 , inf = 0x3f3f3f3f;
const int M = 200010;
int h[N] , q[M];
int n ;
int find(int x)
{
    int t = ((x % N) + N) % N;
    while(h[t] != x && h[t] != inf)
    {
        if(++t == N) t = 0 ;
    }
    return t ;
}
int main()
{
    cin >> n ;
    for(int i = 0 ; i < n ; i++) cin >> q[i] ;
    sort(q,q+n);
    
    memset(h,0x3f, sizeof h);
    
    int res[3] , s[3];
    int rt = 0 , st = 0 ;
    for(int i = 0 ; i < n ; i++)
    {
        for(int j = 0 ; j <= 30 ; j++)
        {
            int d = 1 << j ;
            s[0] = q[i] , st = 1;
            for(int k = 1 ; k <= 2 ; k++)
            {
                int x = q[i] - d * k ;
                if(h[find(x)] == inf) break;
                s[st++] = x ;
            }
            if(rt < st)
            {
                rt = st ;
                memcpy(res,s,sizeof s);
                if(rt == 3) break;
            }
            if(rt == 3) break;
            h[find(q[i])] = q[i];
        }
    }
    cout << rt << endl ;
    for(int i = 0 ; i < rt ; i++)
    {
        cout << res[i] << " " ;
    }
    return 0 ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

如果有任何问题的话，可以私信我或者在底下评论哦 ，写文不易，希望大家多多支持！