logistic回归又称logistic回归分析，是一种广义的线性回归分析模型，常用于数据挖掘，疾病自动诊断，经济预测等领域。例如，探讨引发疾病的危险因素，并根据危险因素预测疾病发生的概率等。以胃癌病情分析为例，选择两组人群，一组是胃癌组，一组是非胃癌组，两组人群必定具有不同的体征与生活方式等。因此因变量就为是否胃癌，值为“是”或“否”，自变量就可以包括很多了，如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的，也可以是分类的。然后通过logistic回归分析，可以得到自变量的权重，从而可以大致了解到底哪些因素是胃癌的危险因素。同时根据该权值可以根据危险因素预测一个人患癌症的可能性。

数据理解和准备

library(MASS)
data(biopsy)
biopsy
1
2
3

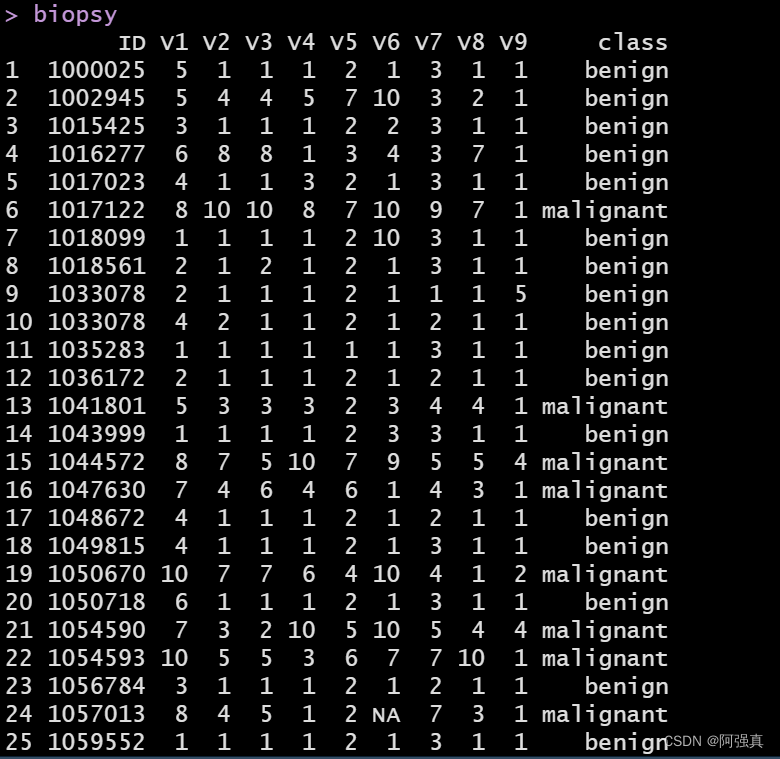
数据集包含699个患者的样本组织，保存在11个变量的数据框中，如下所示：

• ID：样本编码
• V1：细胞浓度
• V2：细胞大小均匀度
• V3：细胞形状均匀度
• V4：边缘黏着度
• V5：单上皮细胞大小
• V6：裸细胞核（16个观测值确实）
• V7：平和染色质
• V8：正常核仁
• V9：有丝分裂状态
• class：肿瘤诊断结果，良性或恶性：这就是我们要预测的结果变量
  首先把样本的编码删除

biopsy$ID=NULL
1

一. 对缺失值的处理

由于缺失值只有16个，占所有观测的2%，所以我们只要删除缺失值即可

biopsy <- na.omit(biopsy)
1

当然你也可以通过插值法来对缺失值进行处理
可以看这篇文章处理缺失值

二.虚拟变量的赋值

考虑将class的两个类别malignant，benign分别赋值为1,0
通过ifelse函数来实现

y <- ifelse(biopsy$class=="malignant",1,0);y
1

三.箱线图

library(tidyverse)
library(reshape2)
biopsy1 <- melt(biopsy,id.var="class");biopsy1
#箱线图
ggplot(biopsy1,aes(class,value))+geom_boxplot(aes(color=variable))+
  facet_wrap(~variable,ncol=3)
1
2
3
4
5
6

四.相关性分析

library(corrplot)
cor(biopsy[,1:9])%>% corrplot.mixed()
1
2

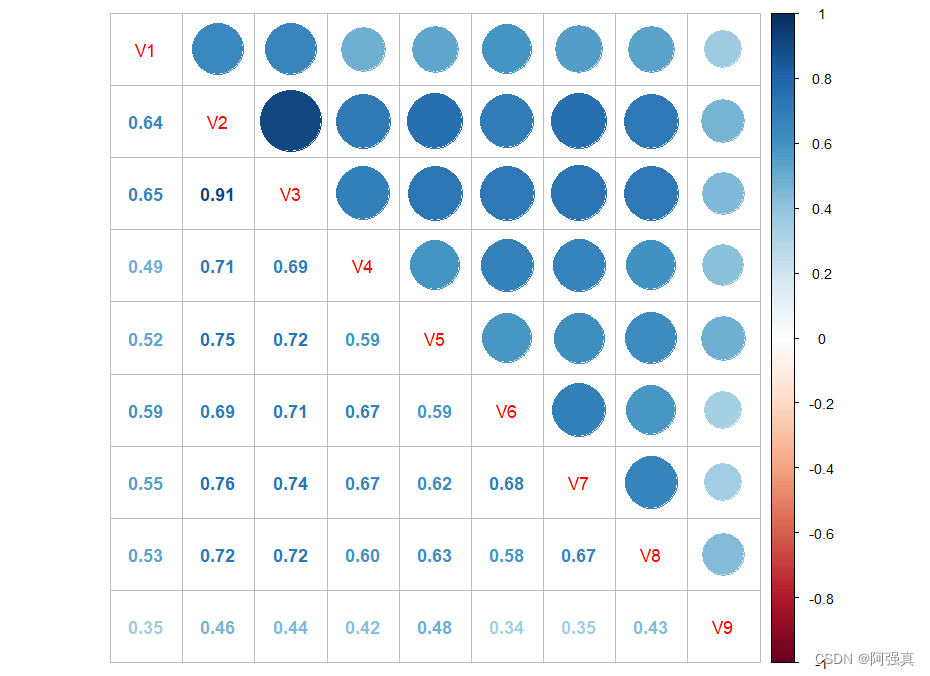
从相关系数可以看出，我们会遇到共线性问题，特别是V2和V3之间的相关系数高达0.91，表现出很明显的共线性

训练集与测试集的划分

有多种方式可以将数据恰当的划分为训练集和测试集：50/50,60/40,70/30,80/20，诸如此类。你应该选择自己的经验和判断选择数据划分方式。在本例中，我选择按照70/30的比例划分数据。如下所示

set.seed(123)
ind <- sample(2,nrow(biopsy1),replace = T,prob=c(0.7,0.3))
ind
train <- biopsy[ind==1,];train
test <- biopsy[ind==2,];test
1
2
3
4
5

为了确保两个数据集的结果变量时均衡的，我们做以下检查

table(train$class)
table(test$class)
1
2

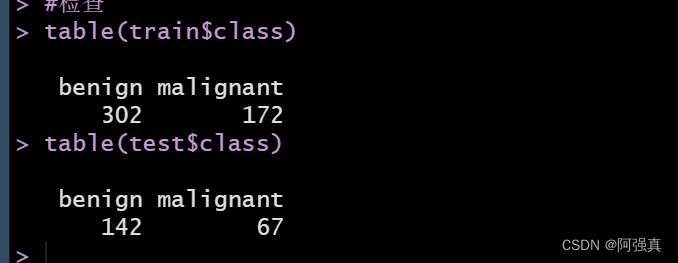
这个内部比例是可以接受的

模型构建与评价

一.logistic回归模型

fit <- glm(class~.,family=binomial,data=train)
summary(fit)
#检查多重共线性
library(car)
vif(fit)
1
2
3
4
5

由于vif值都小于5，可以排除多重共线性的影响

二.检查模型在训练数据集和测试数据集上的表现

首先要建立一个向量表示预测概率：

train.probs <- predict(fit,type="response")
1

下一步需要评价模型在训练集上的效果，然后在评价它在测试集上的拟合程度。
这时我们需要0和1来表示，函数良性区别结果和恶性结果使用的默认值是0.5，也就是说，当概率大于0.5时，就认为这个结果是恶性的

train.probs <- predict(fit,type="response")
train.probs <- ifelse(train.probs >=0.5,1,0)
trainy <- y[ind==1] 
testy <- y[ind==2]
#install.packages("caret")
library(caret)
confusionMatrix(table(trainy, train.probs))
1
2
3
4
5
6
7

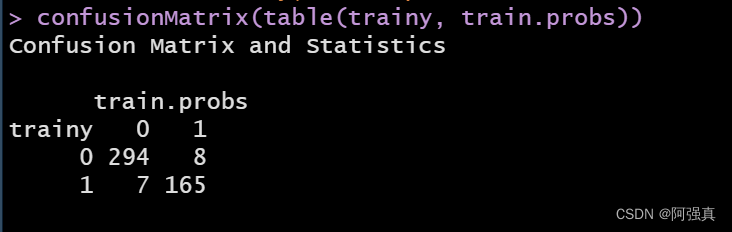
对角线上的就是我们预测错误数值：

error=(7+8)/474;error
1

可以看到预测错误率为0.03
接下来在数据在测试集上的表现：

testy <- y[ind==2]
length(testy)
test.probs <- predict(fit,newdata=test,type="response") #注意这里是newdata
test.probs <-  ifelse(test.probs>=0.5,1,0)
length(test.probs)
confusionMatrix(table(testy, test.probs))
error1 <- (2+3)/209;error1
1
2
3
4
5
6
7

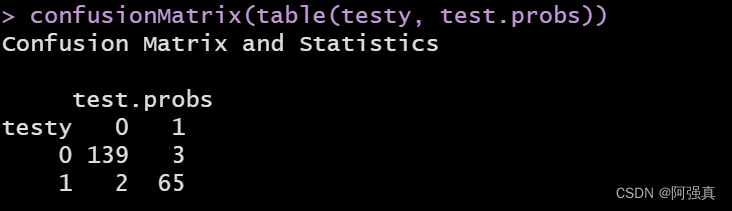
可以看到预测错误率仅为0.02

使用交叉验证的logistic回归

交叉验证
对于原始数据我们要将其一部分分为train data，一部分分为test data。train data用于训练，test data用于测试准确率。在test data上测试的结果叫做validation error。将一个算法作用于一个原始数据，我们不可能只做出随机的划分一次train和test data，然后得到一个validation error，就作为衡量这个算法好坏的标准。因为这样存在偶然性。我们必须好多次的随机的划分train data和test data，分别在其上面算出各自的validation error。这样就有一组validation error，根据这一组validation error，就可以较好的准确的衡量算法的好坏。

Logistic 回归详解 交叉验证概念
我们将用bestglm包进行交叉验证

install.packages("bestglm")
library(bestglm)
X <- train[,1:9]
XY <- data.frame(cbind(X,trainy))
bestglm(Xy=XY,IC="BIC",family=binomial)
1
2
3
4
5

在上面的代码中。Xy=XY指的是我们已经格式化的数据框，IC="BIC"告诉程序我们使用的信息准则为交叉验证

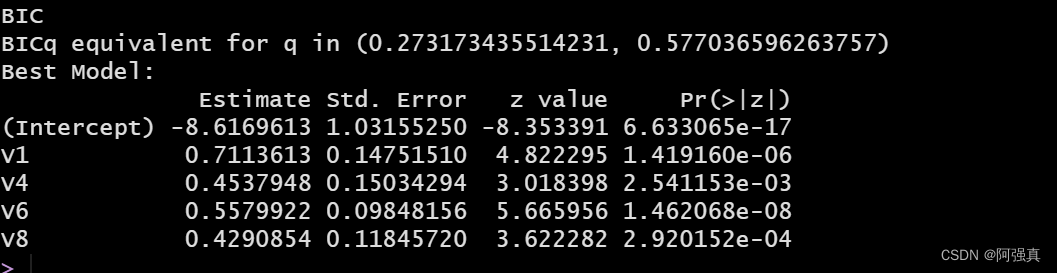
接下来看看BIC最优子集算法的预测效果

bicfit <- glm(class~V1+V4+V6+V8,family=binomial,data=train)
test.bic.probs <- predict(bicfit,family=binomial,newdata=test,
                          type="response")
test.bic.probs <- ifelse(test.bic.probs>=005,1,0)
confusionMatrix(table(testy,test.bic.probs))
1
2
3
4
5

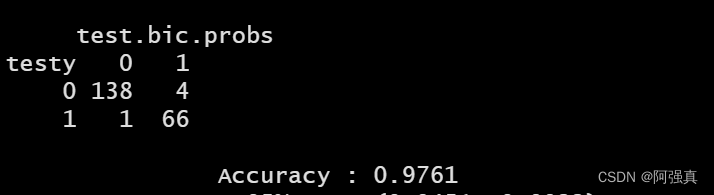
可以看到正确率ACCURACY为0.97