-
Multi-scalar multiplication: state of the art & new ideas
1. 引言
Consensys团队 Gus Gutoski 2020年在zkStudyClub上分享:Multi-scalar multiplication: state of the art & new ideas。
Multi-scalar multiplication(MSM)又名Multi-exponentiation或multi-exp。
针对的场景为:- 参数:某cyclic group G \mathbb{G} G,其order ∣ G ∣ |\mathbb{G}| ∣G∣的bit length为 b b b。(如BLS或BN椭圆曲线,有 ∣ G ∣ ≈ 2 256 |\mathbb{G}|\approx 2^{256} ∣G∣≈2256,即 b = 256 b=256 b=256)
- 输入:
- G \mathbb{G} G内的群元素 G 1 , ⋯ , G n G_1,\cdots,G_n G1,⋯,Gn,称为inputs。
- 整数 a 1 , ⋯ , a n a_1,\cdots,a_n a1,⋯,an的取值范围为 0 0 0到 ∣ G ∣ |\mathbb{G}| ∣G∣,称为scalars。
- 输出:群元素 a 1 G 1 + ⋯ + a n G n a_1G_1+\cdots+a_nG_n a1G1+⋯+anGn称为output。
目标是:
- 减少所需的群运算(+)的次数——为关于 n n n的函数。
直接的解决方案为:
- 使用double-and-add来计算每个 a i G i a_iG_i aiGi,然后将它们相加求和,所需group ops期望值为: 1.5 b n ≈ 1.5 ∗ 256 n ≈ 384 n 1.5bn\approx1.5*256n\approx 384n 1.5bn≈1.5∗256n≈384n
有更优的解决方案么?
1.1 MSM的背景需求
零知识证明ZKP中,Prover向Verifier证明其知道某些 x ⃗ = { a 1 , ⋯ , a n } \vec{x}=\{a_1,\cdots,a_n\} x={a1,⋯,an} secret inputs,使得 P ( x ⃗ ) = y P(\vec{x})=y P(x)=y成立。
在证明过程中,Prover需要使用proving key G 1 , ⋯ , G n G_1,\cdots,G_n G1,⋯,Gn 计算:
G = a 1 G 1 + ⋯ + a n G n G=a_1G_1+\cdots +a_nG_n G=a1G1+⋯+anGn即Prover需要做MSM运算。
- 对于ZCash的NU5升级之前的spend program: n ≈ 4 × 1 0 4 n\approx 4\times 10^4 n≈4×104
- 对于Rollup扩容方案: n n n越大越好
目标是:
- 针对 n = 1 0 7 , 1 0 8 n=10^7,10^8 n=107,108甚至更大的 n n n值。
MSM占据了约 80 % 80\% 80%的Prover工作量。
Justin Drake在2020的Zero-Knowledge podcast Episode 120: ZKPs in Ethereum with Vitalik Buterin & Justin Drake中指出:- Focus on multi-exponentiation, forget about FFTs(Remove the need for FFTs)
- Sparseness
- Recursion
- Custom gates
- Hardware
MSM占据了Prover的主要开销,Prover开销占据ZKP主要开销。改进MSM即意味着提升ZKP效率。
2. bucket method
由Consensys团队开发的:
中采用了bucket算法,针对BLS或BN曲线( b ≈ 256 b\approx 256 b≈256),所需group ops运算次数为:
16 n + ( constant ) 16n+(\text{constant}) 16n+(constant)相比于直接方案的 384 n 384n 384n,性能提升了 24 24 24倍+。
bucket算法详细见2012年论文《Faster batch forgery identification》第4章的“Overlap in the Pippenger approach”,核心策略会:
- 1)将一个 b b b-bit MSM reduce为多个 c c c-bit MSM,其中 c ≤ b c\leq b c≤b。
- 2)使用一些聪明的技巧来计算 c c c-bit MSM。(有趣的部分)
- 3)将多个 c c c-bit MSM合并为最终的 b b b-bit MSM。
3.1 第一步:将一个 b b b-bit MSM reduce为多个 c c c-bit MSM
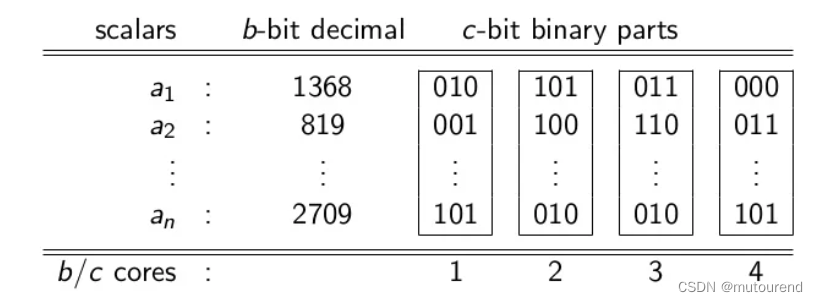
选择 c ≤ b c\leq b c≤b,将每个scalar a 1 , ⋯ , a n a_1,\cdots,a_n a1,⋯,an以二进制表示,将二进制scalar切分为 c c c-bit parts。
如:给定 b = 12 , c = 3 b=12,c=3 b=12,c=3,将每个 12 12 12-bit scalar a a a切分为 3 3 3-bit parts。
若scalar a = 1368 a=1368 a=1368,则将 a a a表示为 a = ( 2 , 3 , 5 , 0 ) a=(2,3,5,0) a=(2,3,5,0):
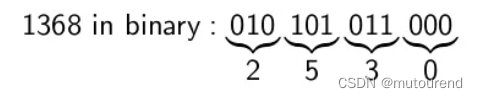
从已切分的scalars推导出 b / c b/c b/c个 c c c-bit MSM instances。
如 ( b , c , b / c ) = ( 12 , 3 , 4 ) (b,c,b/c)=(12,3,4) (b,c,b/c)=(12,3,4),将每个scalar切分表示为 a i = ( a i , 1 , a i , 2 , a i , 3 , a i , 4 ) a_i=(a_{i,1}, a_{i,2}, a_{i,3},a_{i,4}) ai=(ai,1,ai,2,ai,3,ai,4),从而可获得4个 c c c-bit MSM instances T 1 , ⋯ , T 4 T_1,\cdots,T_4 T1,⋯,T4:
T 1 = a 1 , 1 G 1 + ⋯ + a n , 1 G n T_1=a_{1,1}G_1+\cdots +a_{n,1}G_n T1=a1,1G1+⋯+an,1Gn
⋮ \vdots ⋮
T 4 = a 1 , 4 G 1 + ⋯ + a n , 4 G n T_4=a_{1,4}G_1+\cdots +a_{n,4}G_n T4=a1,4G1+⋯+an,4Gn3.2 第三步:将多个 c c c-bit MSM合并为最终的 b b b-bit MSM
常规方法为:double c c c次,然后求和。
仍然以 ( b , c , b / c ) = ( 12 , 3 , 4 ) (b,c,b/c)=(12,3,4) (b,c,b/c)=(12,3,4)为例,合并 T 1 , ⋯ , T 4 T_1,\cdots,T_4 T1,⋯,T4获得最终答案 T T T:- 1)令T=T_1。
- 2)对于
j
=
2
,
⋯
,
4
j=2,\cdots,4
j=2,⋯,4:
- 2.1)令 T = 2 c T T=2^cT T=2cT(double c c c次)
- 2.2)令 T = T + T j T=T+T_j T=T+Tj
最终结果即为 T = a 1 G 1 + ⋯ + a n G n T=a_1G_1+\cdots +a_nG_n T=a1G1+⋯+anGn。
第三步中包含的加法运算开销为:
( b / c − 1 ) × ( c + 1 ) = b − c + b c − 1(b/c−1)×(c+1)=b−c+cb−1( b / c − 1 ) × ( c + 1 ) = b − c + b c − 1 " role="presentation" style="position: relative;">3.3 第二步:使用一些聪明的技巧来计算 c c c-bit MSM
如 ( b , c , b / c ) = ( 12 , 3 , 4 ) (b,c,b/c)=(12,3,4) (b,c,b/c)=(12,3,4),将每个scalar切分表示为 a i = ( a i , 1 , a i , 2 , a i , 3 , a i , 4 ) a_i=(a_{i,1}, a_{i,2}, a_{i,3},a_{i,4}) ai=(ai,1,ai,2,ai,3,ai,4),每个 a i , j a_{i,j} ai,j的取值范围为 1 1 1到 2 c − 1 2^{c}-1 2c−1( 0 0 0值直接忽略,不影响计算结果),对应的取值范围 1 1 1到 2 c − 1 2^{c}-1 2c−1称为bucket,实际的 a i , j a_{i,j} ai,j对应的group G i G_i Gi值放入对应的bucket中,从而有:

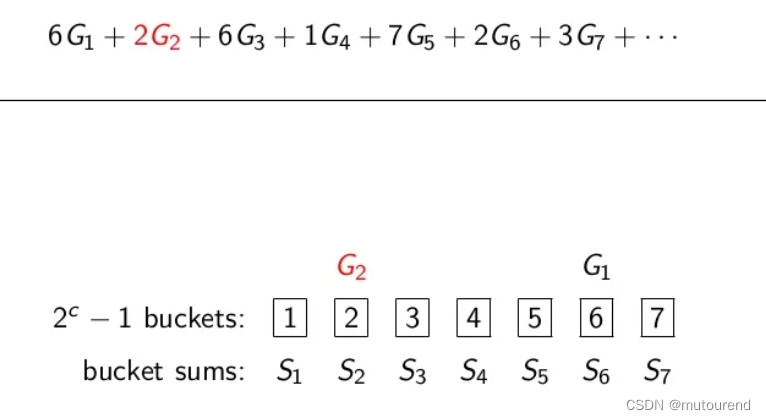
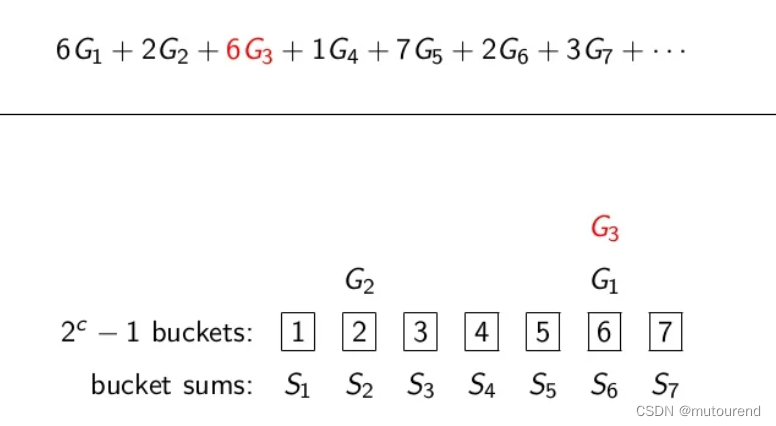
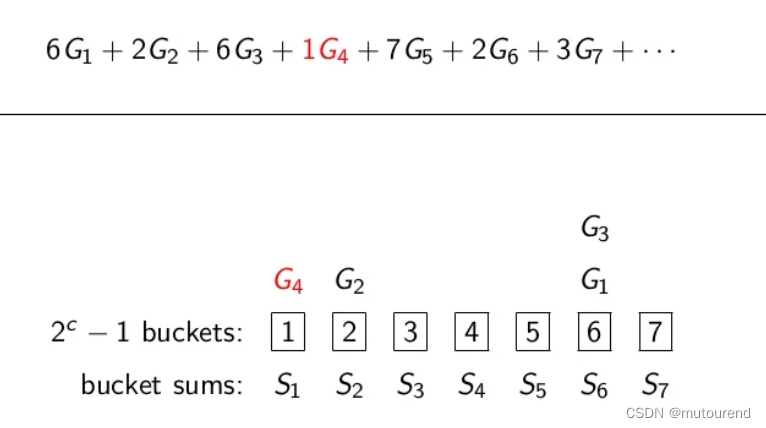

以 n = 14 n=14 n=14为例,将每个bucket求和,相应的 S 1 , S 2 , ⋯ , S 2 c − 1 S_1,S_2,\cdots,S_{2^c-1} S1,S2,⋯,S2c−1为:【所需的加法运算次数为:
n − ( 2 c − 1 ) = n − 2 c + 1n−(2c−1)=n−2c+1n − ( 2 c − 1 ) = n − 2 c + 1 " role="presentation" style="position: relative;">
】

此时, a 1 G 1 + ⋯ a n G n a_1G_1+\cdots a_nG_n a1G1+⋯anGn的结果等价为:
S 1 + 2 S 2 + 3 S 3 + ⋯ + 7 S 7 S_1+2S_2+3S_3+\cdots+7S_7 S1+2S2+3S3+⋯+7S7
这也是一个MSM instance,其中inputs为 S 1 , ⋯ , S 7 S_1,\cdots,S_7 S1,⋯,S7,scalars为 1 , ⋯ , 7 1,\cdots,7 1,⋯,7,且:- inputs数量是固定的,固定为 2 c − 1 2^c-1 2c−1个inputs。
- scalars 1 , ⋯ , 2 c − 1 1,\cdots,2^c-1 1,⋯,2c−1是提前已知的。
快速计算bucket sums S 1 + 2 S 2 + 3 S 3 + ⋯ + 7 S 7 S_1+2S_2+3S_3+\cdots+7S_7 S1+2S2+3S3+⋯+7S7的方法为:
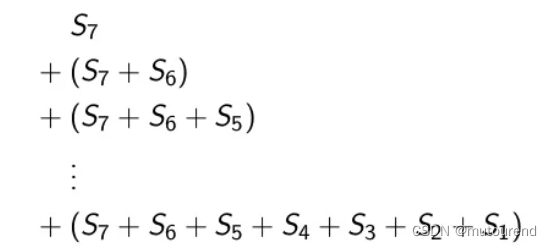
计算 S 1 + 2 S 2 + 3 S 3 + ⋯ + 7 S 7 S_1+2S_2+3S_3+\cdots+7S_7 S1+2S2+3S3+⋯+7S7所需的加法运算次数为:
2 × ( 2 c − 2 ) + 1 = 2 c + 1 − 32×(2c−2)+1=2c+1−32 × ( 2 c − 2 ) + 1 = 2 c + 1 − 3 " role="presentation" style="position: relative;">因此这3步中等式(1)(2)(3),总的加法运算次数为:
( b − c + b c − 1 ) + b c [ ( n − 2 c + 1 ) + ( 2 c + 1 − 3 ) ] = ( b − c + b c − 1 ) + b c ( n + 2 c − 2 ) ≈ b c ( n + 2 c )(b−c+cb−1)+cb[(n−2c+1)+(2c+1−3)]=(b−c+cb−1)+cb(n+2c−2)≈cb(n+2c)( b − c + b c − 1 ) + b c [ ( n − 2 c + 1 ) + ( 2 c + 1 − 3 ) ] = ( b − c + b c − 1 ) + b c ( n + 2 c − 2 ) ≈ b c ( n + 2 c ) " role="presentation" style="position: relative;">当 c ≈ log n c\approx \log n c≈logn时,等式(4)具有最低值。初看,近似scaling为:
O ( b n log n ) O(b\frac{n}{\log n}) O(blognn)注意,必须有 c ≤ b c\leq b c≤b,因此当 n > 2 b n>2^b n>2b时,无法选择 c ≈ log n c\approx \log n c≈logn。
当 n > 2 b n>2^b n>2b时,scaling revert为 O ( n ) O(n) O(n):- 若 b = 1 b=1 b=1,则不可能实现 n log n \frac{n}{\log n} lognn scaling,最好的情况就是 O ( n ) O(n) O(n)。
- 若 b = 256 b=256 b=256,则 n n n永远不可能超过 2 256 2^{256} 2256,因此可实现 n log n \frac{n}{\log n} lognn。
针对等式(4)中的 b c ( n + 2 c ) \frac{b}{c}(n+2^c) cb(n+2c):
- 有large instance n = 1 0 7 n=10^7 n=107,所以 log n ≈ 23 \log n\approx 23 logn≈23。
- gsnark中
b
=
256
b=256
b=256,因此最优性能在
c
=
16
c=16
c=16,实现的开销为:
16 n + ( 2 12 ) 16n+(2^{12}) 16n+(212)
为什么取 c = 16 c=16 c=16,而不是 c = log n c=\log n c=logn呢?原因在于:
- 内存需求scales with 2 c 2^c 2c,因此,内存是瓶颈。
- 若 c c c可被 b b b整除,具有更少的边际情况。
- 如,256-bit scalars存储在4个64-bit limbs中,若 c c c-bit MSM跨坐2个limbs,将是恼人的。
4. 对bucket method的改进
对bucket method的改进措施有:
- 1)可进行并行化处理,这是可行的。
- 2)预计算,除非与后面的措施4结合使用,否则不可行。
- 3)low Hamming-weight表示:不可行。
- 4)【新措施,仅针对椭圆曲线有效】以有符号数字位来表示和概括:可行。
4.1 bucket method的并行加速
采用多核来允许bucket method。
自然的并行分配为:每个 c c c-bit MSM相互独立,类似为:
这样可充分利用 b / c b/c b/c个内核:- 如 ( b , c ) = ( 256 , 16 ) ⇒ 可充分使用 256 / 16 = 16 个内核 (b,c)=(256,16)\Rightarrow 可充分使用256/16=16个内核 (b,c)=(256,16)⇒可充分使用256/16=16个内核。
但是,所需内存也增加了,每个内核都需要 2 c 2^c 2c memory。
当有多于 b / c b/c b/c个内核时,另一种并行分配是:将inputs进行切分:
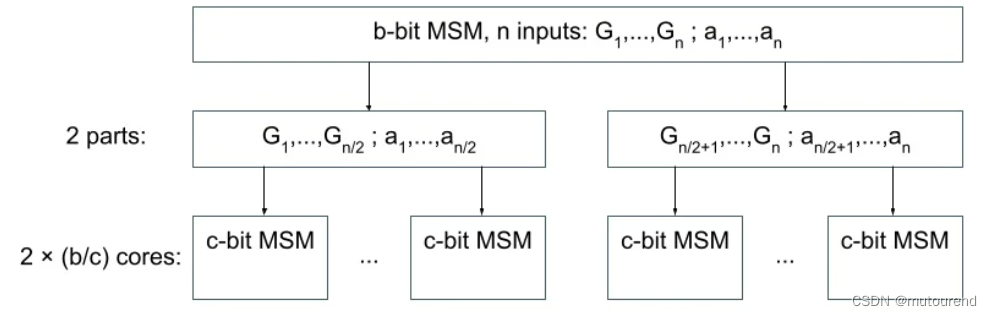
这样分配是inefficiency的:2个size为 n / 2 n/2 n/2的MSM,所需的加法运算次数要多于 1个size为 n n n的MSM。
所以gsnark中并做这种实现,并行化限制为 b / c b/c b/c个核。4.2 对bucket method进行预计算
inputs G 1 , ⋯ , G n G_1,\cdots,G_n G1,⋯,Gn提前已知,可否利用该优势呢?
思路为:预计算并存储a bunch of points,如:- 1)预计算并存储每个input G G G的: 2 G , 3 G , ⋯ , ( 2 c − 1 ) G 2G,3G,\cdots,(2^c-1)G 2G,3G,⋯,(2c−1)G。
- 2)预计算并存储每个input G G G的: 2 k G , 2 2 k G , ⋯ , 2 m k G 2^kG, 2^{2k}G,\cdots,2^{mk}G 2kG,22kG,⋯,2mkG for some k , m k,m k,m。
- 3)预计算并存储各种不同的inputs子集: ( G 1 + G 2 + G 3 ) , ( G 1 + G 2 ) , ( G 1 + G 3 ) , ( G 2 + G 3 ) (G_1+G_2+G_3),(G_1+G_2),(G_1+G_3),(G_2+G_3) (G1+G2+G3),(G1+G2),(G1+G3),(G2+G3)。
目标是:在预计算存储 与 run time之间 取得smooth平衡。
存在的问题是:大的MSM instants以使用了大部分可用内存。- 如,当 n = 1 0 8 n=10^8 n=108时,gsnark需要58GB来存储足够的BLS12-377曲线点啦为具有size- n n n secret input的program生成ZKP。
- 可能可在磁盘上存储额外的点,但磁盘读取可能太慢。需要更多的实验验证。
(1)预计算并存储每个input G G G的: 2 G , 3 G , ⋯ , ( 2 c − 1 ) G 2G,3G,\cdots,(2^c-1)G 2G,3G,⋯,(2c−1)G。
注意, c c c-bit MSM的根本目的是计算 a 1 G 1 + ⋯ + a n G n a_1G_1+\cdots +a_nG_n a1G1+⋯+anGn for b b b-bit scalars a 1 , ⋯ , a n a_1,\cdots,a_n a1,⋯,an。
若 a i G i a_iG_i aiGi已存储,即无需再计算其它的:- 无需计算bucket sum S 1 , ⋯ , S 2 c − 1 S_1,\cdots,S_{2^c-1} S1,⋯,S2c−1;
- 无需对各bucket sum累加求和 S 1 + 2 S 2 + ⋯ + ( 2 c − 1 ) S 2 c − 1 S_1+2S_2+\cdots+(2^c-1)S_{2^c-1} S1+2S2+⋯+(2c−1)S2c−1。
所需的加法运算总次数reduce为:
b c n + ( b − c + b c − 1 ) ≈ b c n \frac{b}{c}n+(b-c+\frac{b}{c}-1)\approx \frac{b}{c}n cbn+(b−c+cb−1)≈cbn所需的额外存储空间为: ( 2 c − 2 ) n (2^c-2)n (2c−2)n:
- 如 b = c = 256 b=c=256 b=c=256,若存储 2 256 n 2^{256}n 2256n个点,仅需要 n n n次加法运算。
- 实际例子 ( n , b , c ) = ( 2 23 , 256 , 16 ) (n,b,c)=(2^{23},256,16) (n,b,c)=(223,256,16),需额外存储5500亿个椭圆曲线点!
(2)在(1)的基础上进行平衡:【不过若存储空间有限,改进有限;若有非常大的存储空间,可由显著改进】

4.3 以low Hamming-weight表示并不能对bucket method加速
针对的是 a G aG aG,单个scalar a a a的计算。
常规是将 a a a以二进制表示,采用double-and-add标准算法,计算开销随 a a a的Hamming weight增加,如以8-bit scalar为例:

针对single-scalar multiplication加速思路有:- 1)采用不同于二进制的表示方法,使scalar具有更低的平均Hamming weight。
如采用non-adjacent form(NAF)表示:

- 2)以double-base number system来表示scalar值:

不过以更低的Hamming-weight表示法并不能改进bucket method的性能:

4.4 引入有符号位表示改进bucket method
新的思路为:利用cheap group inversion。
根源在于:椭圆曲线群逆运算开销几乎为0:- 已知 G ∈ G G\in\mathbb{G} G∈G,计算 − G -G −G为 ( x , y ) ↦ ( x , − y ) (x,y)\mapsto(x,-y) (x,y)↦(x,−y)。
将 c c c-bit的digit set由 { 0 , 1 , ⋯ , 2 c − 1 } \{0,1,\cdots, 2^c-1\} {0,1,⋯,2c−1},改为允许负数的 { − 2 c − 1 , ⋯ , 2 c − 1 − 1 } \{-2^{c-1},\cdots,2^{c-1}-1\} {−2c−1,⋯,2c−1−1}表示:
- 若scalar a > 0 a>0 a>0 for point G G G,则正常向bucket S a S_a Sa添加 G G G。
- 若scalar a < 0 a<0 a<0 for point G G G,则向bucket S ∣ a ∣ S_{|a|} S∣a∣添加 − G -G −G。
- 对于 a > 2 c − 1 a>2^{c-1} a>2c−1,不再需要相应的bucket S a S_a Sa,从而可节约一半的bucket数量。
仍然以3-bit MSM with negative digits为例:





对每个bucket内容求和有:

计算 a 1 G 1 + ⋯ + a n G n a_1G_1+\cdots+a_nG_n a1G1+⋯+anGn等价为计算:
S 1 + 2 S 2 + 3 S 3 + 4 S 4 S_1+2S_2+3S_3+4S_4 S1+2S2+3S3+4S4
相比于之前的 2 c − 1 2^c-1 2c−1个buckets,现在仅需要 2 c − 1 2^{c-1} 2c−1个buckets。
Bucket累加工作跟之前类似,开销由约 2 c 2^c 2c降为了约 2 c − 1 2^{c-1} 2c−1。总的计算开销约为:
b c ( n + 2 c − 1 ) \frac{b}{c}(n+2^{c-1}) cb(n+2c−1)- Option 1:仍选用之前相同的 c c c,可节约50%的bucket的累加开销。
- Option 2:选择
c
=
c
+
1
c=c+1
c=c+1,则可节约一定的总开销,改进量为
c
/
c
+
1
c/c+1
c/c+1,若
c
=
19
c=19
c=19,则对应5%的改进(忽略bucket的累加开销):
b c + 1 ( n + 2 c − 1 ) \frac{b}{c+1}(n+2^{c-1}) c+1b(n+2c−1)
不过,有一些其它原因不建议改变 c c c值。

进一步想象,可便宜计算 ( − 1 ) G (-1)G (−1)G可将bucket累加开销乘以 1 / 2 1/2 1/2因子,若可便宜计算 − μ 1 G , ⋯ , − μ k G -\mu_1G,\cdots,-\mu_kG −μ1G,⋯,−μkG,是否可将bucket累加开销乘以 1 / k 1/k 1/k因子?以 ( c , k ) = ( 16 , 16 ) (c,k)=(16,16) (c,k)=(16,16),MSM性能可提升约20%。

假设可便宜计算 ( − 1 ) G , λ G (-1)G,\lambda G (−1)G,λG:- 可便宜计算 λ G \lambda G λG
- 有 ( μ 1 , μ 2 , μ 3 , μ 4 ) = ( 1 , − 1 , λ , − λ ) (\mu_1,\mu_2,\mu_3,\mu_4)=(1,-1,\lambda,-\lambda) (μ1,μ2,μ3,μ4)=(1,−1,λ,−λ),因此有 k = 4 k=4 k=4而不是2。
从而可使用如下digit set 来表示scalar:

该digit size约为 4 × 2 c 4\times 2^c 4×2c,仅需要约 2 c 2^c 2c个buckets.
此时,引入新的 λ \lambda λ,使得 k k k值double了,不过这种情况并不总有。进一步概括为:

4.4.1 椭圆曲线的cheap multiplication——endomorphism


不过,将scalar转为 λ \lambda λ的digit 表示的开销不容小觑:【 − 1 -1 −1就足够好了,很容易处理overflow的问题】



若可解决将scalar以 λ \lambda λ digit表示的问题,则性能改进还是很客观的,如BLS12-377 ∣ G ∣ |G| ∣G∣为256 bits, λ \lambda λ为128 bits,则可由约50%的性能改进。

4.4.2 如何将scalar值以negative digits表示?



5. 小结



参考资料
[1] Consensys团队 Gus Gutoski 2020年在zkStudyClub上分享:Multi-scalar multiplication: state of the art & new ideas
-
相关阅读:
无胁科技-TVD每日漏洞情报-2022-9-15
SpringBoot整合RocketMQ笔记
【Eclipse】取消按空格自动补全,以及出现没有src的解决办法
Pytorch学习整理笔记(二)
2023最新SSM计算机毕业设计选题大全(附源码+LW)之java智慧医疗问诊系统i0rfv
Kafka 面试八股题整理
《Playing repeated games with Large Language Models》全文翻译
什么是Generator函数?如何使用yield表达式他是干嘛的?next()方法是做什么的?
《大厂面试》之JVM篇21问与答
【unity】【VR】白马VR课堂系列-VR开发核心基础04-主体设置-XR Rig的引入和设置
- 原文地址:https://blog.csdn.net/mutourend/article/details/126207923