队列基本概念

队列（Queue）：是一种只允许在一端插入，在另一端删除的线性表。
我们把允许插入的一端称之为队尾（rear），把允许删除的一端称之为队头（front）。
不含任何数据元素的队列称之为空队列。
队列遵循先进先出（FIFO,first in first out）原则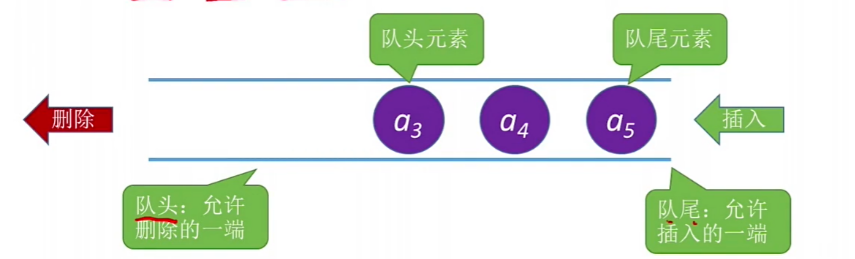

 
生活中的排队就是典型的队列

---

队列的基本操作【只定义函数名】

---

队列的顺序存储实现

1. 顺序队列的结构体

#define MaxSize 10;     //定义队列中元素的最大个数

typedef struct{     
    ElemType data[MaxSize];   //用静态数组存放队列元素     
    int front, rear;          //队头指针和队尾指针
}SqQueue;

void test{     
    SqQueue Q;                //声明一个队列
}
1
2
3
4
5
6
7
8
9
10

2. 顺序队列的初始化：InitQueue(SqQueue &Q)

// 初始化队列
void InitQueue(SqQueue &Q){    
    // 初始化时，队头、队尾指针指向0   
    // 队尾指针指向的是即将插入数据的数组下标  
    // 队头指针指向的是队头元素的数组下标
    Q.rear = Q.front = 0;
}
1
2
3
4
5
6
7

3. 判断队列是否为空：QueueEmpty(SqQueue Q)

bool QueueEmpty(SqQueue Q){     
    if(Q.rear == Q.front)            
        return true;   
    else          
        return false;
}
1
2
3
4
5
6

4. 判断队列是否为满：QueueFull(SqQueue Q) [自己定义]

牺牲最后一个单元，来区分队空和队满

((Q.rear+1) % MaxSize) == Q.front
1

5. 入队（循环队列）：EnQueue(SqQueue &Q, ElemType x)

bool EnQueue(SqQueue &Q, ElemType x){       
    // 如果队列已满直接返回
    if((Q.rear+1)%MaxSize == Q.front) 	//牺牲一个单元区分队空和队满   
        return false;    
    Q.data[Q.rear] = x;   
    Q.rear = (Q.rear+1)%MaxSize; 
    return true;
}
1
2
3
4
5
6
7
8

6. 出队（循环队列）：DeQueue(SqQueue &Q, ElemType &x)

bool DeQueue(SqQueue &Q, ElemType &x){    
    // 如果队列为空直接返回    
    if(Q.rear == Q.front)  
        return false;     
    x = Q.data[Q.front];  
    Q.front = (Q.front+1)%MaxSize;
    return true;
}
1
2
3
4
5
6
7
8

7. 获得队头元素：GetHead(SqQueue &Q, ElemType &x)

bool GetHead(SqQueue &Q, ElemType &x){
    if(Q.rear == Q.front)      
        return false;
    x = Q.data[Q.front];  
    return true;
}
1
2
3
4
5
6

8.求队列元素个数

(rear+MaxSize-front)%MaxSize
1

---

9. !!!【混淆点】：判断是否为空or满的其他方案 !!!

① 解决方法一 ：牺牲一个单元来区分队空和队满

即将(Q.rear+1)%MaxSize == Q.front作为判断队列是否已满，Q.rear == Q.front作为判空的条件。（主流方法，即上面的方法）

② 解决方法二：设置 size 变量记录队列长度

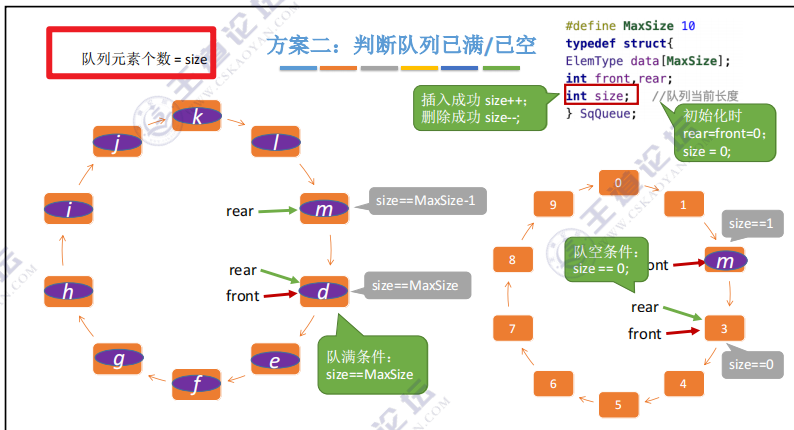
#define MaxSize 10; 

typedef struct{   
    ElemType data[MaxSize]; 
    int front, rear;    
    int size;
}SqQueue;

// 初始化队列
void InitQueue(SqQueue &Q){ 
    Q.rear = Q.front = 0;   
    Q.size = 0;
}

// 判断队列是否为空
bool QueueEmpty(SqQueue 0){     
    if(Q.size == 0)      
        return true;   
    else       
        return false;
}

// 新元素入队
bool EnQueue(SqQueue &Q, ElemType x){ 
    if(Q.size == MaxSize)    
        return false;
    Q.size++; 
    Q.data[Q.rear] = x; 
    Q.rear = (Q.rear+1)%MaxSize;  
    return true;
}

// 出队
bool DeQueue(SqQueue &Q, ElemType &x){   
    if(Q.size == 0)        
        return false;
    Q.size--;
    x = Q.data[Q.front]; 
    Q.front = (Q.front+1)%MaxSize; 
    return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

③ 解决方法三：设置 tag 变量记录队列最近的操作

（tag=0：最近进行的是删除操作；tag=1 ：最近进行的是插入操作）

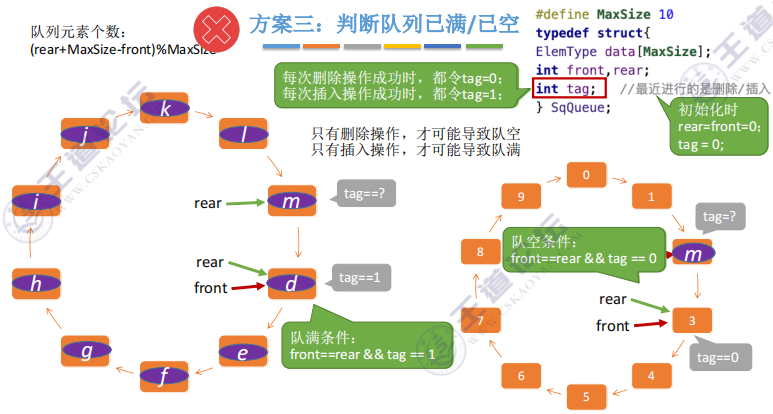
#define MaxSize 10;   

typedef struct{    
    ElemType data[MaxSize]; 
    int front, rear;        
    int tag;
}SqQueue;

// 初始化队列
void InitQueue(SqQueue &Q){    
    Q.rear = Q.front = 0;   
    Q.tag = 0;
}

// 判断队列是否为空
bool QueueEmpty(SqQueue 0){  
    if(Q.front == Q.rear && Q.tag == 0)   
        return true;   
    else       
        return false;
}

// 新元素入队
bool EnQueue(SqQueue &Q, ElemType x){
    if(Q.rear == Q.front && tag == 1)     
        return false;     
    Q.data[Q.rear] = x; 
    Q.rear = (Q.rear+1)%MaxSize;  
    Q.tag = 1;  
    return true;
}

// 出队
bool DeQueue(SqQueue &Q, ElemType &x){
    if(Q.rear == Q.front && tag == 0)  
        return false;   
    x = Q.data[Q.front];
    Q.front = (Q.front+1)%MaxSize; 
    Q.tag = 0;     
    return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

---

队列的链式存储实现

1. 链队列的结构体

// 链式队列结点
typedef struct LinkNode{  
    ElemType data;    
    struct LinkNode *next;
}

// 链式队列
typedef struct{       
    // 头指针和尾指针  
    LinkNode *front, *rear;
}LinkQueue;
1
2
3
4
5
6
7
8
9
10
11

2. 链队列的初始化：InitQueue(LinkQueue &Q)

//带头结点
void InitQueue(LinkQueue &Q){   
    // 初始化时，front、rear都指向头结点 
    Q.front = Q.rear = (LinkNode *)malloc(sizeof(LinkNode));  
    Q.front -> next = NULL;
}



//不带头结点
void InitQueue(LinkQueue &Q){ 
    // 不带头结点的链队列初始化，头指针和尾指针都指向NULL
    Q.front = NULL;   
    Q.rear = NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

3. 判断是否为空：IsEmpty(LinkQueue Q)

//带头结点
bool IsEmpty(LinkQueue Q){ 
    if(Q.front == Q.rear)     
        return true;      
    else         
        return false;
}


//不带头结点
bool IsEmpty(LinkQueue Q){ 
    if(Q.front == NULL)   
        return true;      
    else             
        return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

4. 入队：EnQueue(LinkQueue &Q, ElemType x)

//带头结点
void EnQueue(LinkQueue &Q, ElemType x){ 
    LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode)); 
    s->data = x;  
    s->next = NULL; 
    Q.rear->next = s;  
    Q.rear = s;
}


//不带头结点
void EnQueue(LinkQueue &Q, ElemType x){ 
    LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));  
    s->data = x;   
    s->next = NULL; 
    // 第一个元素入队时需要特别处理   
    if(Q.front == NULL){
        Q.front = s;    
        Q.rear = s; 
    }else{
        Q.rear->next = s;
        Q.rear = s;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

5. 出队：DeQueue(LinkQueue &Q, ElemType &x)

带头结点
不带头结点

//带头结点
bool DeQueue(LinkQueue &Q, ElemType &x){   
    if(Q.front == Q.rear)         
        return false;    
    LinkNode *p = Q.front->next; 
    x = p->data;   
    Q.front->next = p->next; 
    // 如果p是最后一个结点，则将队头指针也指向NULL  
    if(Q.rear == p)          
        Q.rear = Q.front;   
    free(p);     
    return true;
}


//不带头结点
bool DeQueue(LinkQueue &Q, ElemType &x){
    if(Q.front == NULL)
        return false;
    LinkNode *s = Q.front;
    x = s->data;
    if(Q.front == Q.rear){
        Q.front = Q.rear = NULL;
    }else{
        Q.front = Q.front->next;
    }
    free(s);
    return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

---

双端队列

双端队列是允许从两端插入、两端删除的线性表。
如果只使用其中一端的插入、删除操作，则。等同于栈

输入受限的双端队列：允许一端插入，两端删除的线性表。
输出受限的双端队列：允许一端删除，两端插入的线性表。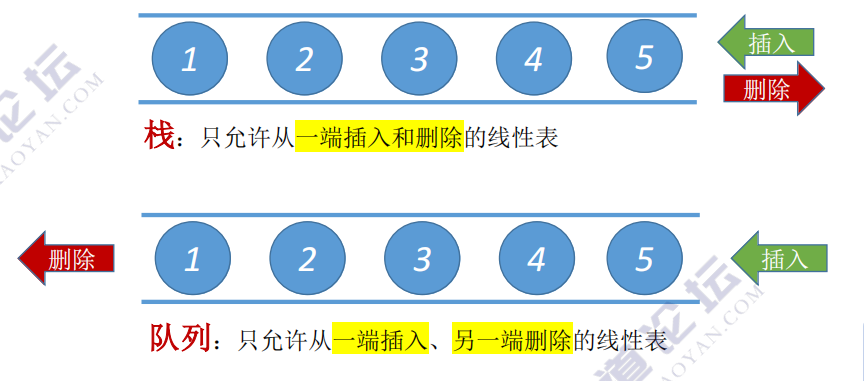

考点：判断输出序列的合法化

• 例：数据元素输入序列为 1，2，3，4，判断 4! = 24 个输出序列的合法性

栈中合法的序列，双端队列中一定也合法