1.算术三元组的数目

1）题目描述

给你一个下标从 0 开始、严格递增 的整数数组 nums 和一个正整数 diff 。如果满足下述全部条件，则三元组 (i, j, k) 就是一个 算术三元组 ：

• i < j < k ，
• nums[j] - nums[i] == diff 且
• nums[k] - nums[j] == diff
  返回不同 算术三元组 的数目。

2）原题链接

3）思路解析

$(1)$数据范围很小，直接暴力枚举即可

4）模板代码

 public int arithmeticTriplets(int[] arr, int diff) {
        int ans=0;
        int n=arr.length;
        for (int i = 0; i <=n-3; i++) {
            for (int j = i+1; j <=n-2; j++) {
                for (int k = j+1; k <=n-1; k++) {
                    if (arr[j]-arr[i]==diff&&arr[k]-arr[j]==diff) ans++;
                }
            }
        }
        return ans;
    }
1
2
3
4
5
6
7
8
9
10
11
12

5）算法与时间复杂度

  算法：暴力枚举
  时间复杂度:$O(n^3)$

2.受限条件下可到达节点的数目

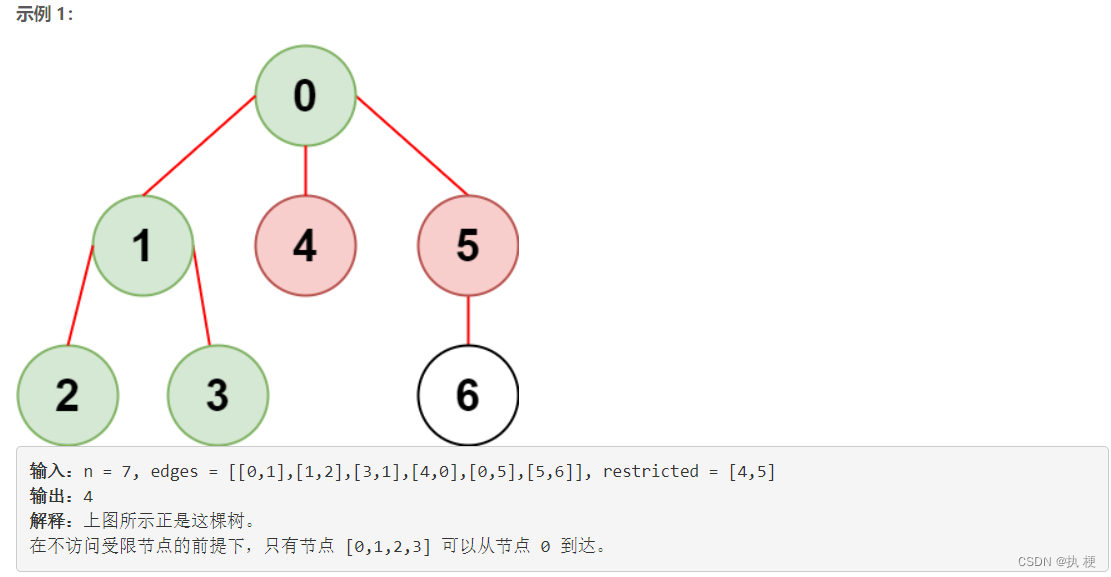
1）题目描述

现有一棵由 n个节点组成的无向树，节点编号从0 到n - 1 ，共有n - 1条边。

给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restricted 表示 受限 节点。

在不访问受限节点的前提下，返回你可以从节点 0 到达的 最多 节点数目。

注意，节点 0 不会标记为受限节点。

2）原题链接

3）思路解析

$(1)$很模板的搜索题，从0开始进行深搜或者广搜都非常简单，当然dfs的代码更加简洁，也可用使用并查集，不过比较麻烦。

4）模板代码

 Map<Integer, List<Integer>> map=new HashMap<>();
    Set<Integer> set=new HashSet<>();
    int ans=0;
    public int reachableNodes(int n, int[][] edges, int[] restricted) {
        
        for (int v:restricted) set.add(v);
        for (int[] a:edges){
            add(a[0],a[1]);
            add(a[1],a[0]);
        }
        dfs(0,-1);
        return ans;
    }
    void dfs(int u,int fa){
        ans++;
        if (!map.containsKey(u)) return;
        for (int h:map.get(u)){
            if (set.contains(h)||h==fa) continue;
            dfs(h,u);
        }
    }
    void  add(int a,int b){
        if (!map.containsKey(a)) map.put(a,new LinkedList<>());
        map.get(a).add(b);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

5）算法与时间复杂度

  算法：搜索
  时间复杂度:最坏情况下$O(n)$，每个点最多被搜索一次。

3.检查数组是否存在有效划分

1）题目描述

给你一个下标从 0 开始的整数数组 nums ，你必须将数组划分为一个或多个 连续 子数组。

如果获得的这些子数组中每个都能满足下述条件 之一 ，则可以称其为数组的一种 有效 划分：

1. 子数组 恰 由 2 个相等元素组成，例如，子数组 [2,2] 。
2. 子数组 恰 由 3 个相等元素组成，例如，子数组[4,4,4]。
3. 子数组 恰 由 3 个连续递增元素组成，并且相邻元素之间的差值为 1 。例如，子数组 [3,4,5] ，但是子数组[1,3,5]不符合要求。

如果数组 至少 存在一种有效划分，返回 true ，否则，返回 false 。

2）原题链接

3）思路解析

• $(1)$比如入门的dp题，如果能想到dp的话就非常好写了，定义$f[i]$为只考虑前$i$个元素是否能进行有效划分。
• $(2)$考虑初始化，首先$f[0]$肯定为true，0个元素肯定是有效情况。$f[1]$肯定为false。
• $(3)$考虑状态转移，只考虑数组中第$i$个元素，那么由转移方程
  $$f[i]=\{\begin{array}{ll}f[i]|=f[i-2]& \text{if a[i-1]==a[i-2]}\\ f[i]|=f[i-3]& \text{if a[i-1]==a[i-2]\&\&a[i-2]==a[i-3]}\\ f[i]|=f[i-3]& \text{if a[i-1]+a[i-3]==a[i-2]*2\&\&a[i-1]-2==a[i-3]}\end{array}$$
  当这三种情况满足任意一种时，$f[i]$均为true。当然后面两种要在i>=3的情况下才可判断，最终答案就为f[n]的值。

4）模板代码

  public boolean validPartition(int[] arr) {
        int n=arr.length;
        boolean[] f=new boolean[n+1];
        f[0]=true;
        for (int i = 2; i<=n; i++) {
            int x=i-1;
            if (arr[x]==arr[x-1]) f[i]|=f[i-2];
            if (i>2){
                if (arr[x]==arr[x-1]&&arr[x-1]==arr[x-2]) f[i]|=f[i-3];
                if (arr[x]+arr[x-2]==arr[x-1]*2&&arr[x]-2==arr[x-2]) f[i]|=f[i-3];
            }
        }
        return f[n];
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14

5）算法与时间复杂度

  算法：动态规划
  时间复杂度:$O(n)$

4.最长理想子序列

1）题目描述

给你一个由小写字母组成的字符串 s ，和一个整数 k 。如果满足下述条件，则可以将字符串 t 视作是 理想字符串 ：

• t是字符串 s 的一个子序列。
• t 中每两个 相邻 字母在字母表中位次的绝对差值小于或等于 k 。
  返回 最长 理想字符串的长度。

字符串的子序列同样是一个字符串，并且子序列还满足：可以经由其他字符串删除某些字符（也可以不删除）但不改变剩余字符的顺序得到。

注意：字母表顺序不会循环。例如，'a' 和'z'在字母表中位次的绝对差值是 25 ，而不是 1 。

2）原题链接

3）思路解析

• $(1)$同样考虑dp解决问题，问题在于如果我们定义f[i]的含义是考虑前i个字符可形成的最长理想字符串长度，这样每次转移的话需要考虑前面所有的字母，这样复杂度会达到$O(n^2)$，1e5的复杂度定然是不可取的。
• $(2)$考虑到这是一个字符串，我们可以定义$f[i]$为以字符i结尾的最长理想字符串长度。所以我们只需要开一个长度为26的数组来映射26个字母即可。
• $(3)$考虑状态转移，当第i个字符的ASCII码为x时，能让第i个字符合法转移的字符的ASCII的区间则为$[x-k,x+k]$。那么当j处于$[x-k,x+k]$区间时，则有转移方程:
  $$f[i]=max(f[j]+1,f[i])$$
  这里需要注意的是，一个字符一定是可以从与它相同的字符转移过来的，也就是说对于$f[i]$的答案，我们需要先记录下来，否则在$[x+k]$这个区间转移时会在再次转移导致答案错误。

4）模板代码

class Solution {
 int[] f=new int[26];
    public int longestIdealString(String s, int k) {
        char[] c=s.toCharArray();
        int len=c.length;
        for (int i = 0; i <len ; i++) {
            int g=c[i]-'a';
            int start=Math.max(0,g-k);
            int end=Math.min(25,g+k);
            int v=f[g];
            for (int j = start; j <=end; j++) {
                v=Math.max(f[j]+1,v);
            }
            f[g]=v;
        }
        int ans=0;
        for (int i = 0; i < 26; i++) {
            ans=Math.max(ans,f[i]);
        }
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

5）算法与时间复杂度

  算法：动态规划
  时间复杂度:$O(nk)$