基本算法——直接选择排序

​
​

活动地址：CSDN21天学习挑战赛

​

学习的最大理由是想摆脱平庸，早一天就多一份人生的精彩；迟一天就多一天平庸的困扰。各位小伙伴，如果您：
想系统/深入学习某技术知识点…
一个人摸索学习很难坚持，想组团高效学习…
想写博客但无从下手，急需写作干货注入能量…
热爱写作，愿意让自己成为更好的人…
…
欢迎参与CSDN学习挑战赛，成为更好的自己，请参考活动中各位优质专栏博主的免费高质量专栏资源（这部分优质资源是活动限时免费开放喔~），按照自身的学习领域和学习进度学习并记录自己的学习过程。您可以从以下3个方面任选其一着手（不强制），或者按照自己的理解发布专栏学习作品，参考如下：

**

创作计划

**
1，机缘

早年就加了群主大大的好友和交流群，那个时候是在刚读大学本科的时候，现在马上也该研二了~~~

2，收获

A，巩固大佬专栏中的基本算法
B，能够让自己写的内容帮助到一部分人
C，认识志同道合的领域同行
…

3，日常

提示：当前创作和你的工作、学习是什么样的关系 例如：

1. 偶尔会写博客记录自己学习的内容
2. 大部分时间没养成写博客的习惯，希望今后遇到问题解决问题都做记录分享给大家

4，憧憬

提示：不想去互联网公司卷，惜命哈哈哈，希望找个稳定一点的工作，过幸福安稳的生活就好~~

学习计划

1，学习目标

每篇博客使用自己习惯的编程语言实现至少一个算法

2，今日学习内容

A，了解直接插入排序的概念
B，使用编程实现该算法

3，学习时间

周一至周五晚上 7 点—晚上9点

4，学习产出

CSDN技术博客 1 篇

学习日记

1.选择排序的概念：

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理是：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。

它也可以被划分为两个区域进行理解：

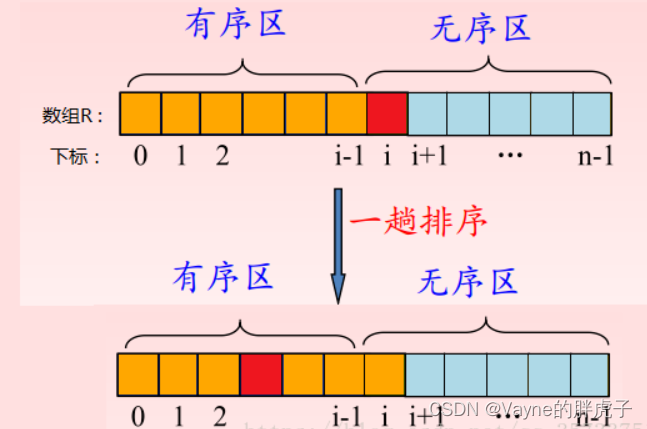
①初始状态：无序区为R[0…n-1]（共n个元素），有序区为空。 [1]
②第1趟排序
设置一个变量i，让i从0至n-2循环的同时，在对比数组中元素i跟元素i+1的大小，如果R[i+1]比R[i]小，则用一个变量k来记住他的位置（即k=i+1）。等到循环结束的时候，我们应该找到了R中最小的那个数的位置了。然后进行判断，如果这个最小元素的不是R的第一个元素，就让第一个元素跟他交换一下值，使R[0…0]和R[1…n-1]分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区。
……
③第i趟排序
第i趟排序开始时，当前有序区和无序区分别为R[0…i-1]和R[i…n-1]。该趟排序从当前无序区中选出关键字最小的记录 R[k]，将它与无序区的第1个记录R交换，使R[0…i]和R分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区。

2.举例说明

现在有一组待排序的初始关键字序列为{49 , 38 , 15 , 17 , 16 , 13 , 27 , 49}，直接选择排序过程如下：

step1：

先找到最小值13，将其放到列表的第一个位置：

step2：

除掉第一个元素13，往后在无序区里面找最小值，找到了15，放在第二个位置，如下图所示：

step3：

除掉排好序的前两个元素，往后在无序区里面找最小值，找到了16，放在第三个位置，如下图所示：

下面的过程就以此类推，不再一一画出来了，大家只要知道原理就可以了，下面是直接选择排序的代码实现了：

3.代码实现版本1（python）：

def direct_select_sort(l):
    for i in range(len(l) - 1):
        min_val = l[i]
        for j in range(i + 1, len(l)):
            if l[j] <= min_val:
                min_val = l[j]
        min_index = l.index(min_val)
        # l[i],l[l.index(min_val)] = l[l.index(min_val)],l[i]
        # l[l.index(min_val)], l[i] = l[i], l[l.index(min_val)]
        l[i], l[min_index] = l[min_index], l[i]
        print(l)
    # print(l)


l = [49, 38, 15, 17, 16]
direct_select_sort(l)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

注意：上面的代码中两行被注释的交换元素的代码在python语言中按道理都是成立的，但是大家运行之后会发现里面有一行不能完成排序操作，大家想知道为什么的可以参考下面这个帖子：

https://blog.csdn.net/Liz_Jiang/article/details/80705011

另外上面这个代码如果列表中有重复的元素也会有bug，因为原理是根据索引值查找的第一个最小值，如果这样就会打乱已经排好序的元素，我们可以使用第二个版本的代码优化：

原理是：每一次选出最值之后，将搜索的列表只局限在无序区中，这样下标就不会定位到有序区中已经排序好的元素了。

4.代码实现版本2（python）：

def direct_select_sort(l):
    for i in range(len(l) - 1):
        min_val = l[i]
        for j in range(i + 1, len(l)):
            if l[j] <= min_val:
                min_val = l[j]
        min_index = l[i:].index(min_val)
        l[i], l[min_index + i] = l[min_index + i], l[i]
        print(l)
    # print(l)


l = [17, 49, 38, 15, 15, 17, 16]
direct_select_sort(l)
1
2
3
4
5
6
7
8
9
10
11
12
13
14

我们还可以只记录下标，这样会更加容易理解：

5.代码实现版本3（python）：

def direct_select_sort(l):
    for i in range(len(l) - 1):
        min_val = i
        for j in range(i + 1, len(l)):
            if l[j] <= l[min_val]:
                min_val = j
        l[i],l[min_val]=l[min_val],l[i]

        # print(l)
    print(l)


l = [17, 49, 38, 15, 15, 17, 16]
direct_select_sort(l)
1
2
3
4
5
6
7
8
9
10
11
12
13
14

6.算法性能

6.1时间复杂度

选择排序的交换操作介于 0 和 (n - 1)次之间。选择排序的比较操作为 n (n - 1） / 2 次之间。选择排序的赋值操作介于 0 和 3 (n - 1） 次之间。比较次数O(n^2），比较次数与关键字的初始状态无关，总的比较次数N=(n-1）+(n-2）+…+1=n*(n-1）/2。交换次数O(n），最好情况是，已经有序，交换0次；最坏情况交换n-1次，逆序交换n/2次。交换次数比冒泡排序少多了，由于交换所需CPU时间比比较所需的CPU时间多，n值较小时，选择排序比冒泡排序快。

6.2稳定性

选择排序是给每个位置选择当前元素最小的，比如给第一个位置选择最小的，在剩余元素里面给第二个元素选择第二小的，依次类推，直到第n-1个元素，第n个元素不用选择了，因为只剩下它一个最大的元素了。那么，在一趟选择，如果一个元素比当前元素小，而该小的元素又出现在一个和当前元素相等的元素后面，那么交换后稳定性就被破坏了。举个例子，序列5 8 5 2 9，我们知道第一遍选择第1个元素5会和2交换，那么原序列中两个5的相对前后顺序就被破坏了，所以选择排序是一个不稳定的排序算法。