将任意一组非线性增长的数均匀映射至0到1上

如果有一组线性增长且刚好在[0, 1]内的数[0, 0.25, 0.5, 0.75, 1]，那么不需要任何计算，这几个数就是均匀分布在0到1内的。假设x从0递增到1，每次加0.01，任意时刻它的结果y∈[0, 1]就等于x。当x走到0.25时刚好在[0, 1]的四分之一处，x走到0.5时刚好在二分之一处，任何人都可以直接看出来。其实这里也有个映射关系的，就是y=x * 1，因为乘以1可以省略，所以看起来就是x没做任何计算就均匀映射到[0, 1]内了。这么简单的东西，实际上还是有点用的。

接着来看第二组数，也是线性增长，但不是在[0, 1]范围内的[0, 2, 4, 6, 8]，x从0增到8，每次加0.1，那么任意时刻的x映射到[0, 1]的结果y，就为y=x / 8。也就是当x走到2时刚好在y的四分之一处，走到4时刚好在y的二分之一处。因为x是线性增长的，所以要将[0, 8]映射到[0, 1]内，就是[0 / 8 = 0, 8 / 8 = 1]。也就是将[0, 2, 4, 6, 8]均匀映射到[0, 1]的映射关系就是y=x / 8，结合上面那一步，完整的映射关系应该是y=x / 8 * 1。

说完了上面那两步，就可以回到标题说的那个问题上了。假设有一组非线性增长的数[0, 2, 3, 9, 14]。线性增长的意思，可以看做：当前的数减去它前一个数，等于它后一个数减去当前的数。而这组数显然是不符合这条件的。如果还要将这组数均匀的映射到[0, 1]内，也就是x从0增到14，每次加0.1，当x走到2时要刚好在[0, 1]四份之一处，走到3时要在二分之一处，走到9时在四分之三处，走到14刚好就是1。那直接用第二步的方法的话，0除以14确实为0，14除以14也确实为1，但是3/14并不等于1/2，是无法达到效果的。当然解决办法还是有的，几行代码就可以搞定。当一个问题无法解决时，可以将其转化为已解决的问题，然后用已知的方法把未解决的问题给解决掉。[0, 2, 3, 9, 14]无法直接映射到[0, 1]，但是可以先把它转换成[0, 1, 2, 3, 4]这样一组线性增长的数，将这组数映射到[0, 1]内那不是简简单单，直接套用第二步的方法[0 / 4 = 0, 4 / 4 = 0]得到映射关系就是y=x / 4。那[0, 2, 3, 9, 14]怎么转换成[0, 1, 2, 3, 4]，其实也不难，通过观察，就可以得到：0、2、3、9、14在数组里的下标，就是0、1、2、3、4，也就是当x走到2时，就可以得到1，走到3时得到2，当然这不是计算出来的，而是固定死的对应关系。但是还有一个问题，x每次加0.1，某一时刻x走到了1，那这个1怎么对应到[0, 1, 2, 3, 4]内呢？还是通过观察，1在0-2的中间，也就是占了0.5，那0-1的0.5还是0.5，x为2.1时在2-3之间占了0.1，那1-2的0.1就是1.1，总结成一般规律就是x - i / j - i，i和j都是[0, 2, 3, 9, 14]中的一个数且i <= x <= j。知道了这两个对应关系，就可以将任意一组非线性增长的数[0, n]转换成一组线性增长的数，再将这组线性增长的数均匀映射到[0, 1]内，最终结果就把这组非线性增长的数均匀映射到[0, 1]内了。因为是非线性的，所以无法通过一个等式就把映射关系表达出来，看代码：

  1 #include <stdio.h>
  2 
  3 static float to_linear(
  4     int* arr, int arr_len, float value, int last, float result
  5 ) {
  6     if (arr_len == 0) {
  7         return result;
  8     }
  9     if (value > arr[0]) { // 这个if里头就是相当于将[0, 2, 3, 9, 14]转换成[0, 1, 2, 3, 4]，得到整数部分
 10         result++;
 11         last = arr[0];
 12         arr++;
 13         arr_len--;
 14         return to_linear(arr, arr_len, value, last, result);
 15     } else { // else里头则计算小数部分，当value不是0/1/2/3/4这几个数时，此时的value应该是[0, 4]的哪个部分
 16         return result + (value - last) / (arr[0] - last);
 17     }
 18 }
 19 
 20 static float to_linear01(float value, int arr_len) {
 21     return value / arr_len; // 这里相当于将转换成线性的[0, 4]后，再将结果映射为[0, 1]内的数
 22 }
 23 
 24 int main(int argc, char** args)
 25 {
 26     int arr[4] = {2, 3, 9, 14};
 27     for (double x = 0.f; x < 14.1f; x += 0.10f) {
 28         float value = to_linear(arr, 4, x, 0, 0);
 29         value = to_linear01(value, 4);
 30         printf("x为:%.2f时，映射到[0, 1]内的:%.2f\n", x, value);
 31     }
 32     return 0;
 33 }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

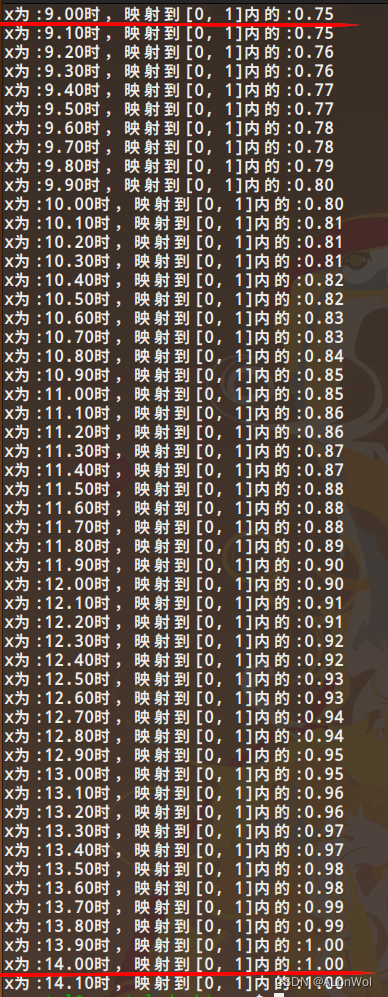
编译执行，可以看到结果：当x为0时，对应[0, 1]的0，x为2时，对应[0, 1]的四分之一处，x为3时，对应[0, 1]的二分之一处，x为9时，对应[0, 1]的四分之三处，x为14时，刚好就是1了。中间部分，x为不同值时，结果有些是重复的，就是因为给定的那组数不是线性增长的。如果给一组线性增长的数，调用该接口，那么得到的结果就不会重复了，同时也是线性增长的。可以换成任意数量，线性或非线性增长的一组数，调用接口就可以均匀映射到[0, 1]内了（注意接口对应参数要做相应修改！）。