线性代数学习笔记6-1：行列式与线性变换

行列式：用面积的变化描述线性变换的效果

之前说过，线性变换就是一种操纵空间和变换坐标轴的手段，它保持原点固定且网格平行等距；
有的线性变换将空间拉伸，有的线性变换将空间向内挤压（如剪切/切变变换），有的甚至将空间压缩至维度降低（对应的矩阵中列向量线性相关）

那么，如何衡量线性变换对空间的拉伸/压缩效果呢？或者更具体的，给定一个区域，如何测量其面积增大/缩小的比例呢？

• 我们只考虑一个1x1的单位正方形（即两个基向量围成的区域）面积变化的情况
  
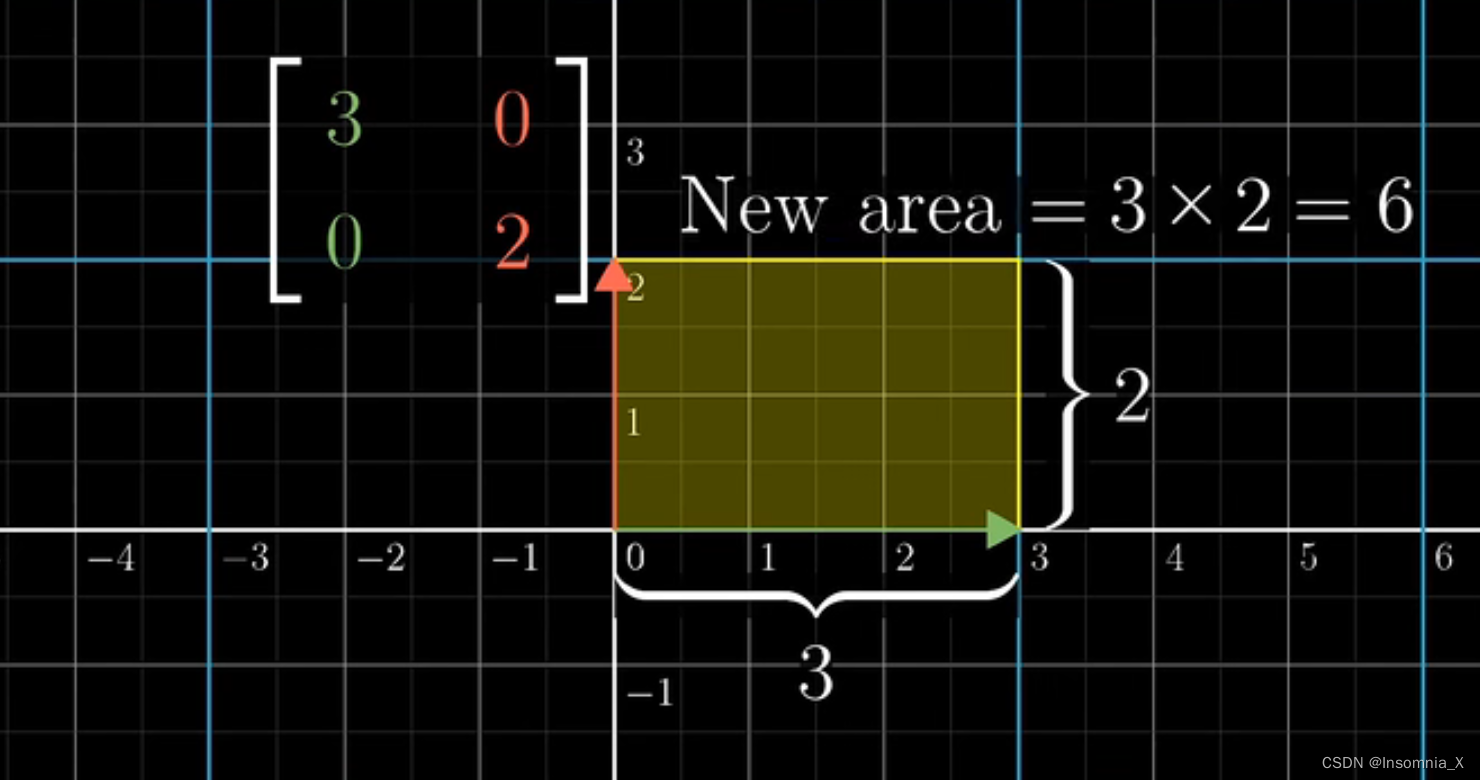
  可见，经过一个线性变换后，其面积变为3x2=6倍
• 一般的，这种面积缩放的比例如何计算呢？——用行列式
  
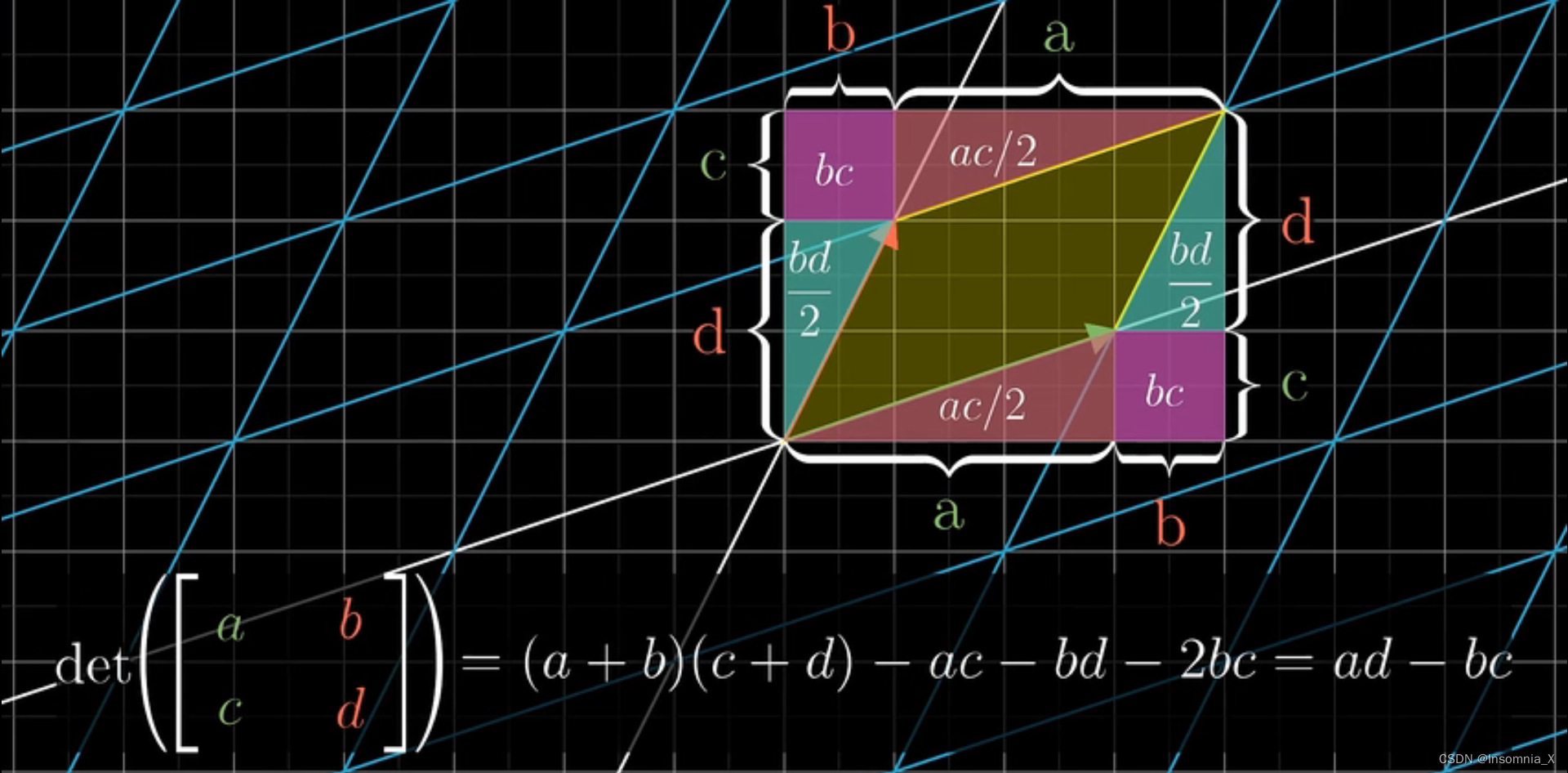
  上图证明了，矩阵行列式determinant（的绝对值），就是相应线性变换后任一区域的面积变化比例
• 那考虑其他区域面积的变化情况呢？
  实际上，上面的1x1正方形的面积变化已经说明了一切：
  ①其他矩形区域的面积变化比例与之相同（这是由于线性变换的比例性决定的）；
  ②而对于一般的不规则区域，可以用微分思想，将其视作由无数不规则的小正方形组成，面积变化比例也与正方形相同。

行列式为何有正负？

行列式为负值，一个区域如何缩放“负数倍”呢？
实际上，这与数学上的定向Orientation的概念有关。

• 对于二维空间，原来的基向量$\mathbf{i}$位于$\mathbf{j}$的右侧，如果线性变换后，${\mathbf{i}}^{\prime }$位于${\mathbf{j}}^{\prime }$的左侧，这就改变了空间的定向（理解为一张纸被翻转到另一面，感觉像这个变化让空间“翻转”了），此时行列式为负值
• 对于三维空间同理，原来三个基向量满足坐标系的右手定则，如果变换后不满足了，则空间的定向被改变，此时行列式为负值

如何直观理解空间定向的改变与行列式负值（负的面积改变）的关系呢？
考虑二维空间中的一个剪切变换：
$\mathbf{i}$轴逐渐靠近$\mathbf{j}$轴，过程中空间不断被压缩，因此行列式为正值且不断减小；
当两个轴重合，此时的变换使得空间降维至一条线，所有面积变为0，因此行列式为0；
$\mathbf{i}$轴继续逆时针转动，逐渐远离$\mathbf{j}$轴，空间定向改变，行列式继续减小为负值，但是过程中空间又扩张了，因此行列式绝对值（面积变化比例）又开始增大了

总之，严格来说，行列式表示有向面积/有向体积（三维时就是体积）的变化比例
或者说，行列式的绝对值表示相应几何图形的面积/体积，其中，这个几何图形的所有边由行列式的行/列向量给出（理解为：原来在标准正交坐标系，坐标轴围成的几何图形的面积/体积为1，故变化比例=线性变换后的图形面积/体积）

行列式为0

根据上面的讨论，行列式为0（i.e. 面积变化比例为0）说明面积被压缩为0，也就是说，空间被压缩至降维！那么对应的矩阵必然列线性相关（变换后有多余基向量无法张成更高维空间，也即基向量线性相关）

注意前提：方阵才有行列式！

几何意义：

• 当变换前后，空间的维度相同（变换矩阵是方阵），我们考虑“有向面积/体积”的变化比例才有意义
• 如果变换后，空间维度已经被压缩（变换矩阵不是方阵），那就没必要看行列式了
  （少一个维度怎么谈论“体积”呢？或着，可以简单理解为此时“行列式”即面积缩放比例为0，没必要再讨论了）

总结

• 矩阵的行列式是一个数，它衡量了线性变换对于空间的拉伸/压缩效果
• 行列式表示有向面积/有向体积（三维时就是体积）的变化比例
  行列式的正负：表示空间定向是否改变
  行列式的绝对值：表示面积/体积的缩放比例
• 用几何的思想理解行列式是有意义的，例如可以简单的证明$det({\mathbf{M}}_1{\mathbf{M}}_2)=det({\mathbf{M}}_1)det({\mathbf{M}}_2)$