一、寻找峰值

题目链接

描述：

给定一个长度为n的数组nums，请你找到峰值并返回其索引。数组可能包含多个峰值，在这种情况下，返回任何一个所在位置即可。
1.峰值元素是指其值严格大于左右相邻值的元素。严格大于即不能有等于
2.假设 nums[-1] = nums[n] = −∞
3.对于所有有效的 i 都有 nums[i] != nums[i + 1]
4.你可以使用O(logN)的时间复杂度实现此问题吗？

数据范围：

1≤nums.length≤2×10^5
−2 ^31<=nums[i]<=2 ^31−1

如输入[2,4,1,2,7,8,4]时，会形成两个山峰，一个是索引为1，峰值为4的山峰，另一个是索引为5，峰值为8的山峰，如下图所示：

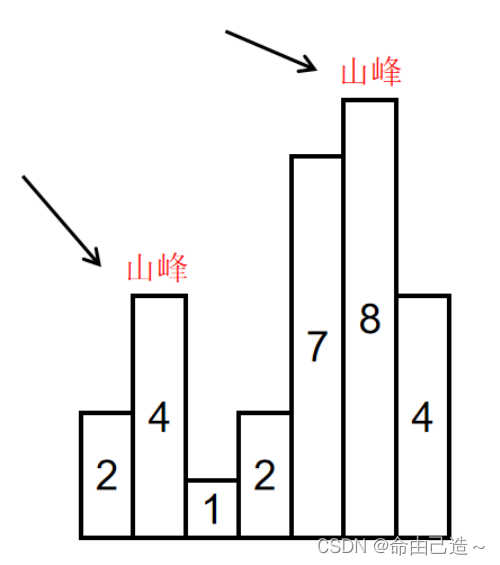
示例1

输入：[2,4,1,2,7,8,4]
返回值：1
说明：4和8都是峰值元素，返回4的索引1或者8的索引5都可以

示例2

输入：[1,2,3,1]
返回值：2
说明：3 是峰值元素，返回其索引 2

思路分析：
这里用到了二分查找的性质，因为数组两边都是无穷小，所以我们只要往高处找就一定能找到波峰。那么我们就可以找一个元素，把数组分成两个区间，每次就走高的一边，最后就能锁定出一个波峰。

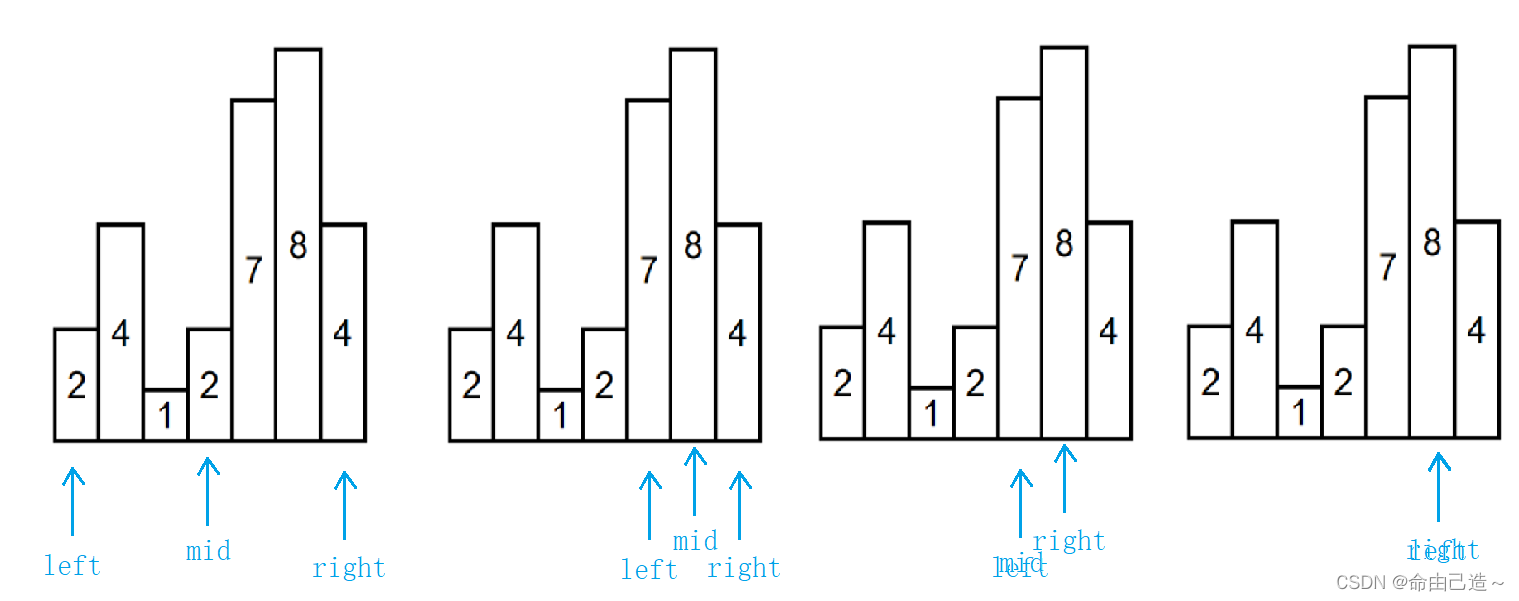
int findPeakElement(int* nums, int numsLen ) {
    // write code here
    int left = 0, right = numsLen - 1;
    while(left < right)
    {
        int mid = (left + right) / 2;
        //右边是往下，不一定有坡峰
        if(nums[mid] > nums[mid + 1])
        {
            right = mid;
        }  
        //右边是往上，一定能找到波峰
        else
        {
            left = mid + 1;
        }
    }
    return left;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

---

二、二维数组中的查找

题目链接
描述：

在一个二维数组array中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。
[
[1,2,8,9],
[2,4,9,12],
[4,7,10,13],
[6,8,11,15]
]
给定 target = 7，返回 true。
给定 target = 3，返回 false。

数据范围：矩阵的长宽满足 0≤n，m≤500，矩阵中的值满足0≤val≤10^9
进阶：空间复杂度 O(1)O(1) ，时间复杂度 O(n+m)O(n+m)

示例1

输入：7,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]]
返回值：true
说明：存在7，返回true

示例2：

输入：1,[[2]]
返回值：false

示例3

输入：3,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]]
返回值：false
说明：不存在3，返回false

① 线性搜索

最简单的方法就是暴力遍历，没有用到二维数组的递增性质。
通过规律发现左下角所在元素的所在行最小，所在列最大，那么如果target小于所在元素，就让行--，否则就让列++。

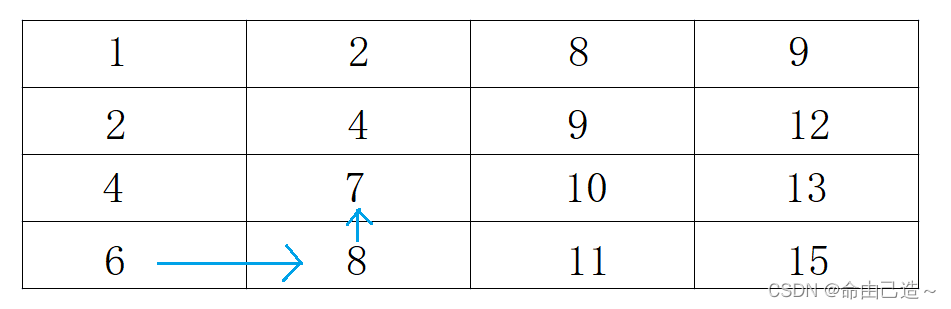
bool Find(int target, int** array, int arrayRowLen, int* arrayColLen ) {
    // write code here
    int row = arrayRowLen - 1, col = 0;
    while(row <= arrayRowLen - 1 && row >= 0 && col <= *arrayColLen - 1 && col >= 0)
    {
        if(array[row][col] == target)
        {
            return true;
        }
        else
        {
            if(array[row][col] < target)
            {
                col++;
            }
            else
            {
                row--;
            }
        }
    }
    return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

② 逐行二分

因为每一行都是有序递增的，所以每一行都能用二分

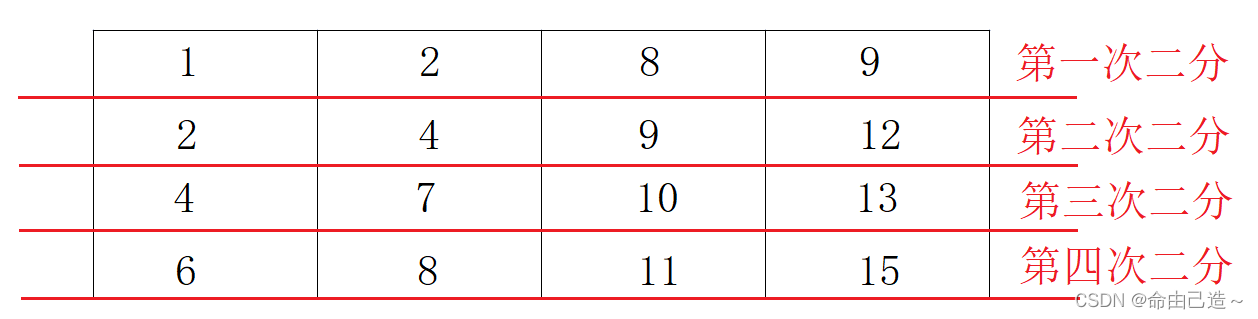
bool binary_search(int* arr, int k, int target)
{
    int left = 0, right = k - 1;
    while (left <= right)
    {
        int mid = (right + left) / 2;
        if (arr[mid] == target)
        {
            return true;
        }
        else if (arr[mid] > target)
        {
            right = mid - 1;
        }
        else
        {
            left = mid + 1;
        }
    }
    return false;
}



bool Find(int target, int** array, int arrayRowLen, int* arrayColLen) {
    // write code here
    for (int i = 0; i < arrayRowLen; i++)
    {
        if (binary_search(array[i], *arrayColLen, target))
        {
            return true;
        }
    }
   /*while (arrayRowLen--)
    {
        if (binary_search(*array, *arrayColLen, target))
        {
            return true;
        }
        array++;
    }*/
    return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

三、旋转数组的最小数字

题目链接

描述：

有一个长度为 n 的非降序数组，比如[1,2,3,4,5]，将它进行旋转，即把一个数组最开始的若干个元素搬到数组的末尾，变成一个旋转数组，比如变成了[3,4,5,1,2]，或者[4,5,1,2,3]这样的。请问，给定这样一个旋转数组，求数组中的最小值。

数据范围：1≤n≤10000，数组中任意元素的值:0≤val≤10000
要求：空间复杂度：O(1)O(1) ，时间复杂度：O(logn)O(logn)

示例1:

输入：[3,4,5,1,2]
返回值：1

示例2:

输入：[3,100,200,3]
返回值：3

思路分析：
这道题其实是二分法的变形，旋转点左边的元素都单调递增且都大于旋转点右边单调递增的元素。
我们的目的是找到旋转点也就是最小的元素，我们可以定义左left、右right指针让他们相遇在旋转点：
当arr[mid] > arr[right]时
说明mid一定在左递增区间，为了使left移动到旋转点就需要缩小区间，left = mid + 1
当arr[mid] < arr[right]时
说明mid一定在右递增区间，为了使right移动到旋转点就需要缩小区间，right = mid
但是也有相同元素的情况，例如：｛1，0，1，1，1｝
这样就无法判断mid在哪个区间了。
那么就让right--，这里不能让left++，因为我们是跟最右边的元素比较,旋转点一定在mid左边。

int minNumberInRotateArray(int* arr, int sz ) {
    // write code here
    if(sz == 0)
    {
        return 0;
    }
    int left = 0, right = sz - 1;
    while(left < right)
    {
        int mid = (left + right) / 2;
        if(arr[mid] > arr[right])
        {
            left = mid + 1;
        }
        else if(arr[mid] < arr[right])
        {
            right = mid;
        }
        else
        {
            right--;
        }
    }
    return arr[left];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25