TI mmWave radar sensors Tutorial 笔记 | Module 5: Angle Estimation

本系列为TI(Texas Instruments) mmWave radar sensors 系列视频公开课 的学习笔记。

• 视频网址: https://training.ti.com/intro-mmwave-sensing-fmcw-radars-module-1-range-estimation?context=1128486-1139153-1128542

• 关注 下面的公众号，回复“ TI毫米波 ”，即可获取 本系列完整的pdf笔记文件~

---

内容在CSDN和微信公众号同步更新

• CSDN博客
• 微信公众号

• Markdown源文件暂未开源
• 笔记难免存在问题，欢迎联系指正

FMCW Radars – Module 1 : Range Estimation
FMCW Radars – Module 2 : The Phase of the IF Signal
FMCW Radars – Module 3 : Velocity Estimation
FMCW Radars – Module 4 : Some System Design Topics
FMCW Radars – Module 5 : Angle Estimation

Module 5 Angle Estimation

• Content
  • Angle Estimation of a single object
  • Field of view
  • Angle resolution
  • Discussion on Range, Velocity and Angle Resolution

This module: to answer the following question

• 1 How does the radar estimate the angle of arrival of an object in front of the radar?
• 2 What if there are multiple objects at different angles ?
• 3 What determines the maximum field of view ?
• 4 What does the angle resolution depend on?

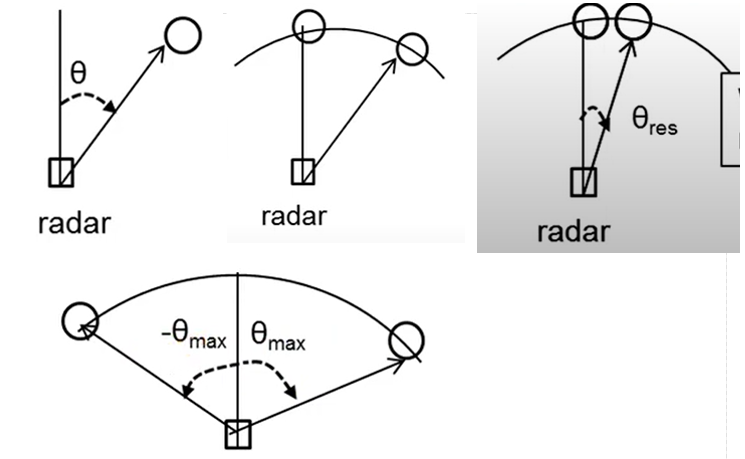
Basis of Angle of Arrival (AoA) estimation

• Recall:
  • a small change in the distance of the object $\Rightarrow$
  • result in a phase change ($\omega$) in the peak of the range-FFT

• Angle Estimation :
  • requires at least 2 RX antennas
  • 不同天线回波由于角度不同会存在距离差, results in a phase change in the 2D-FFT peak, 从而计算出AoA

Question: Why are these two expressions off by a factor of 2?

• 因为 $\Delta \Phi =2\pi f_c\Delta \tau$
• 而这里的 $\Delta \tau =\Delta d/c$ , instead of $\Delta \tau =2\Delta d/c$

How to measure the AoA of an object using 2 RX antennas?

• TX antenna transmits a frame of chirps

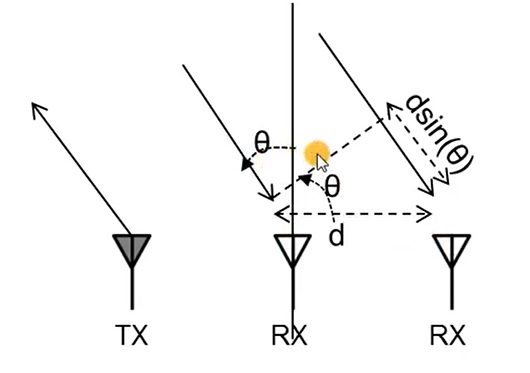
• The 2D-FFT corresponding to each RX antenna will have peaks in the same location but with differing phase
  • 如下图

• The measured phase difference $(\omega )$ can be used to estimate the AoA of the object
  • $\omega =\frac{2\pi dsin(\theta )}{\lambda }$
  • $\Rightarrow$ $\theta =si{n}^{-1}(\frac{\lambda \omega }{2\pi d})$

Estimation accuracy depends $AoA$

• Note that the relationship between $\omega$ and $\theta$ is non-linear
  • unlike in the case of velocity ($\omega =\frac{4\pi v{T}_c}{\lambda }$)
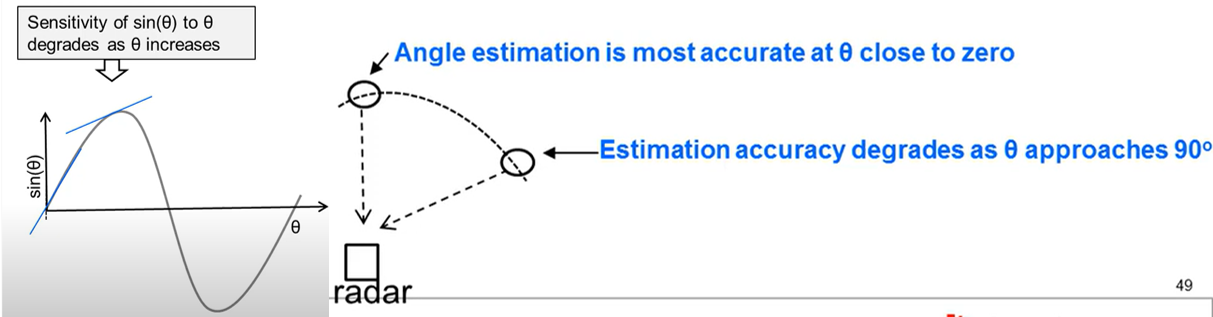
• 非线性的影响：
  • At $\theta =0$, $\omega$ is most sensitive to changes in $\theta$
  • Hence: estimation of $\theta$ is more error prone as $\theta$ increases

Angular Field of View

• 如下图，同样是$|\omega |<180^{\circ }$
  • Unambiguous only if $|\omega |<180^{\circ }$

• Unambiguous measurement of angle:
  • $\Rightarrow$ $|\omega |<180^{\circ }$
  • $\frac{2\pi d sin(\theta)}{\lambda} < \pi < / f o n t > ∗ ∗ ∗ ∗ < f o n t c o l o r = g r e e n f a c e = " C o m i c S a n s M S , S T X i n w e i " > ** ** </font>∗∗∗∗<fontcolor=greenface="ComicSansMS,STXinwei">\Rightarrow < / f o n t > ∗ ∗ ∗ ∗ < f o n t c o l o r = r e d f a c e = " S e g o e P r i n t , S T K a i t i " > ** ** </font>∗∗∗∗<fontcolor=redface="SegoePrint,STKaiti">\theta < sin^{-1} (\frac{\lambda}{2d})$

结论：

• The maximum FoV that can be serviced by two antennas spaced $d$ apart is:
  • ${\theta }_{max}=si{n}^{-1}(\frac{\lambda }{2d})$
  • if spacing $d=\lambda /2$ results in the largest FoV: ±90 ${}^{\circ }$
    (注意这里符号d的含义)

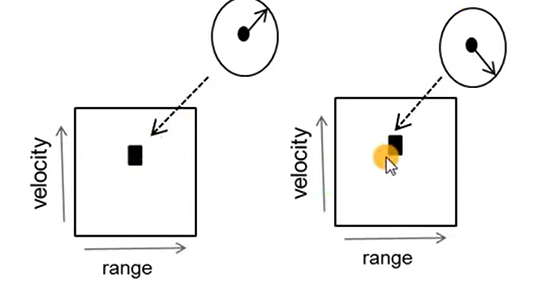
Measuring AoA of multiple objects at the same range and velocity

• Consider two objects equidistant from the radar approaching the radar at the same relative speed to the radar
  • The value at the peak has phasor components from both objects
  • $\Rightarrow$ Hence previous approach will not work

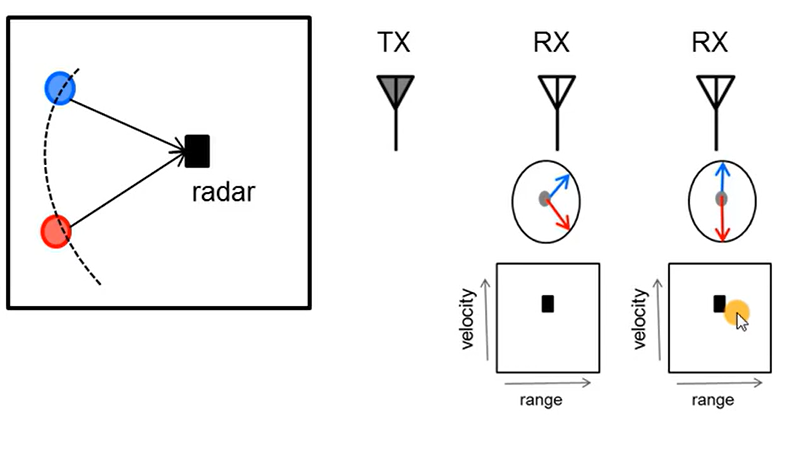
• Solution :
  • An FFT on the sequence of phasors corresponding to the 2D-FFT peaks resolves the two objects
  • $\Rightarrow$ angle-FFT
  • ${\omega }_1$ and ${\omega }_2$ correspond to the phase difference between consecutive chirps for the respective objects

结论 ：

• ${\theta }_1=si{n}^{-1}(\frac{\lambda {\omega }_1}{2\pi d})$
• ${\theta }_2=si{n}^{-1}(\frac{\lambda {\omega }_2}{2\pi d})$

Angle Resolution

• Angle Resolution :
  • Two objects at AOA’s of $\theta$ and $\theta +\Delta \theta$
  • How small can $\Delta \theta$ can get?
• Use the following:
  • An object with an AOA of $\theta$ has a discrete frequency of $\omega =\frac{2\pi dsin(\theta )}{\lambda }$ in the angle-FFT
  • Criterion for separation in the frequency domain: $\Delta \omega >\frac{2\pi }{N}$
  • N: the number of samples in the FFT
• 推导：
  • $\Delta \omega =\frac{2\pi d}{\lambda }(sin(\theta +\Delta \theta )-sin(\theta ))\approx \frac{2\pi d}{\lambda }(cos(\theta )\Delta \theta )$
  • 因为$sin(\theta )$的derivative是$cos(\theta )$
  • $\Rightarrow$ $\Delta \omega >\frac{2\pi }{N}$
  • $\Rightarrow$ $\Delta \theta >\frac{\lambda }{Ndcos(\theta )}$

结论 ：

• Angle resolution given by: ${\theta }_{res}=\frac{\lambda }{Ndcos(\theta )}$
• Resolution is often quoted assuming $d=\lambda /2$ and $\theta =0$ $\Rightarrow$ ${\theta }_{res}=2/N$

Note 1 :

• 角度分辨率与角度$\theta$有关
  • Resolution best at $\theta =0$
• Resolution degrades as AoA increases (如下图)

Comparison of Angle & Velocity Estimation

• 角度 和 速度估计 存在很多相似的地方，可以对比

• Angle Estimation:

  • 基于：天线的 空间分离
  • 分辨率${\theta }_{res}=\frac{\lambda }{Ndcos(\theta )}$，分辨率取决于 孔径(空间)大小
  • 最大测量角度(${\theta }_{max}=\frac{\lambda }{2d}$)取决于天线间的 空间距离$d$

• 速度估计

  • 基于chirps的 时间分离
  • 分辨率$v_{res}=\frac{\lambda }{2T_f}$ 取决于 帧(时间)长度
  • 最大测量速度$\frac{\lambda }{T_c}$取决于chirps的 时间间隔$T_c$

Angle Estimation in FMCW radar

• A single TX, RX chain can estimate the range and velocity of multiple objects
• localization / imaging: 需要 range + angle
  • angle estimation: needs Multiple RX antennass
  • The 2D FFT grid is generated at each RX chain (correpsonding to each antenna)
  • FFT on the corresponding peak across antennas is used to estimate the angle

系列完结 End