---

一：什么是线段树？

线段树的概念： 线段树是算法竞赛中常用的用来维护 区间信息 的数据结构。

线段树可以在 $O(logN)$ 的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。

---

二：线段树的基本结构及空间复杂度

线段树的结构（文字解释）：

• 线段树将每个长度不为 $1$ 的区间划分成左右两个区间递归求解，把整个线段划分为一个树形结构，
• 线段树的操作通过合并左右两区间信息来求得该区间的信息。这种数据结构可以方便的进行大部分的区间操作。
• 线段树为满二叉树，用一维数组存整颗树

线段树的结构（下图所示）：

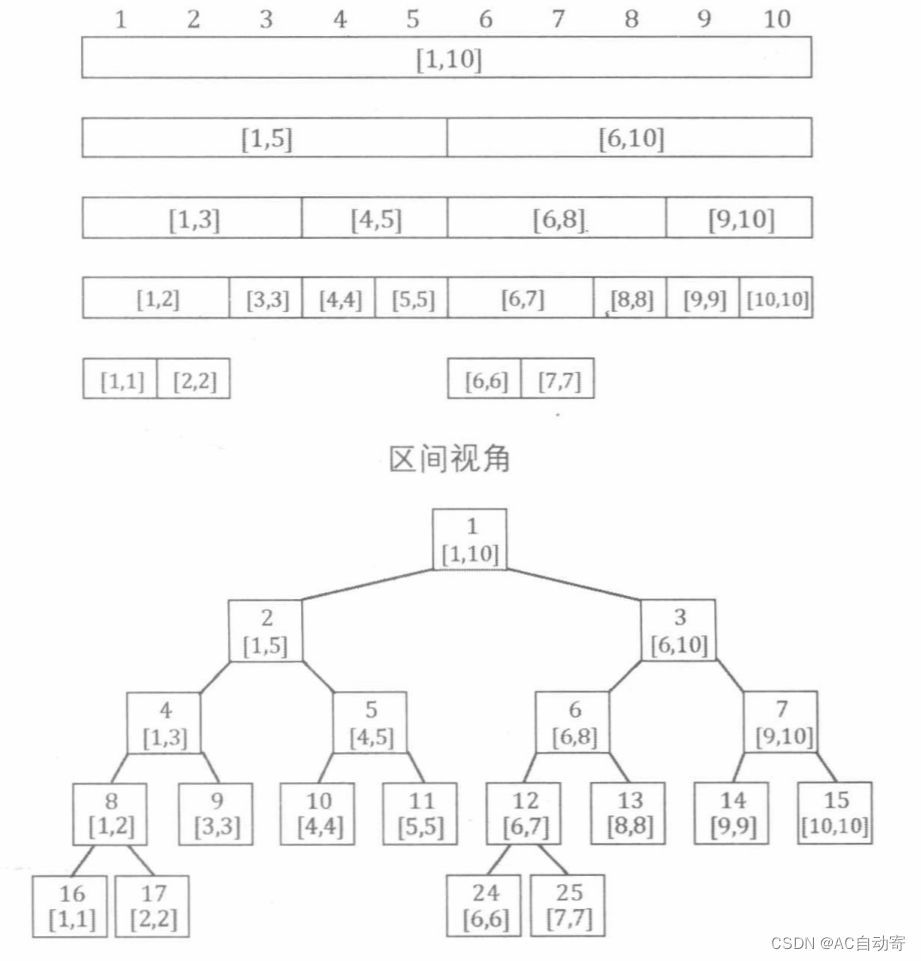
线段树的空间复杂度：

对于线段树最少要开4倍空间的解释：

• 若最后一层节点都满，则该层为最后一层，有$N$个节点，则其上面节点数为 $N/2+N/4+N/8+......+1$，此时所有节点数为 $N+N/2+N/4+N/8+......+1$ 和为 $2N-1$
• 若最后一层不满，即、上两图所示的情况，则倒数第二层为 $N个节点$，除倒数第一层以外的所有层节点和为 $2N-1$，最后一层为 $2N$ 个节点，即、总节点为 $4N-1$ ，所以保险起见，线段树一律开 $4N$ 空间

---

三：线段树的常用操作

线段树的建树

线段树的节点关系：

• 若该节点为 x
• 其父节点为 x / 2等效于x >> 1
• 左儿子为 x * 2等效于x << 1
• 右儿子为 x * 2 + 1等效于x << 1 | 1

---

常用函数：

• $pushup()$
• $pushdown()$
• $build()$
• $modify()$
• $query()$

1.pushup() 更新操作（子->父）

在介绍 $build()$ 函数之前先介绍 $pushup()$ 函数；

$pushup()$函数含义为：由子节点信息更新父节点信息

例子：单点修改（求最大值，最小值等 …)

---

2.pushdown() 更新操作（父->子）

**俗称：**懒标记（支持区间修改）
以区间加为例：
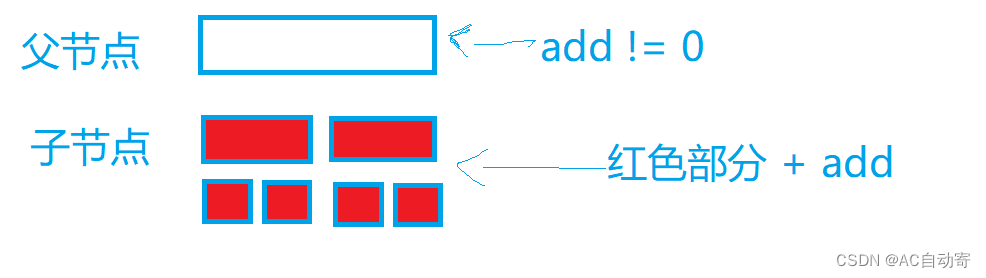
含义： 给当前区间的所有儿子加上 add(懒标记)
如图：

---

3.build() 建树操作

建立线段树：

• 从根节点开始，一层层递归到叶子节点
• 每递归一层调用一次 $pushup()(由子节点更新父节点)$

一般模板为：

函数参数为：当前区间的编号u 当前区间的左端点l 当前区间的右端点r

void build(int u, int l, int r)
{
	tr[u] = {l, r};
	if(l == r) return;
	int mid = l + r >> 1;
	build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
	pushup(u);
}

1
2
3
4
5
6
7
8
9
10
11
12

---

3.modify() 修改操作

• 单点修改操作：一直递归至叶子节点，在返回时 $pushup()$ 即可
• 区间修改操作：和 $query()$函数 类似，每次分裂前 $pushdown()$ ，返回时 $pushup()$

---

4.query() 查询操作

以查询区间最大值为例：
其中 $[L,R]$ 为 要查询的区间，$[T_L,T_R]$ 为当前区间的范围

则有如下几种情况：

1. $[L,R]\supset [T_L,T_R]$
2. $[L,R]\cap [T_L,T_R]\ne \varnothing$
3. $[L,R]\cap [T_L,T_R]=\varnothing$

具体操作：

1. $[L,R]\supset [T_L,T_R]$
如图：

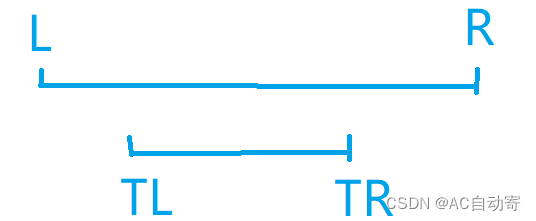
即、树中区间在我们要查询区间的内部：直接返回最大值（树中保存的信息即可）

2. $[L,R]\cap [T_L,T_R]\ne \varnothing$
如图:

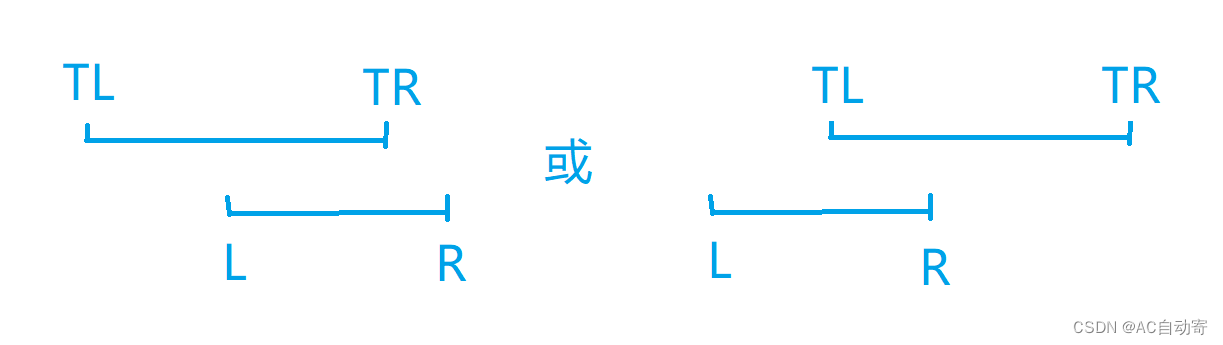
包含如下几种情况：



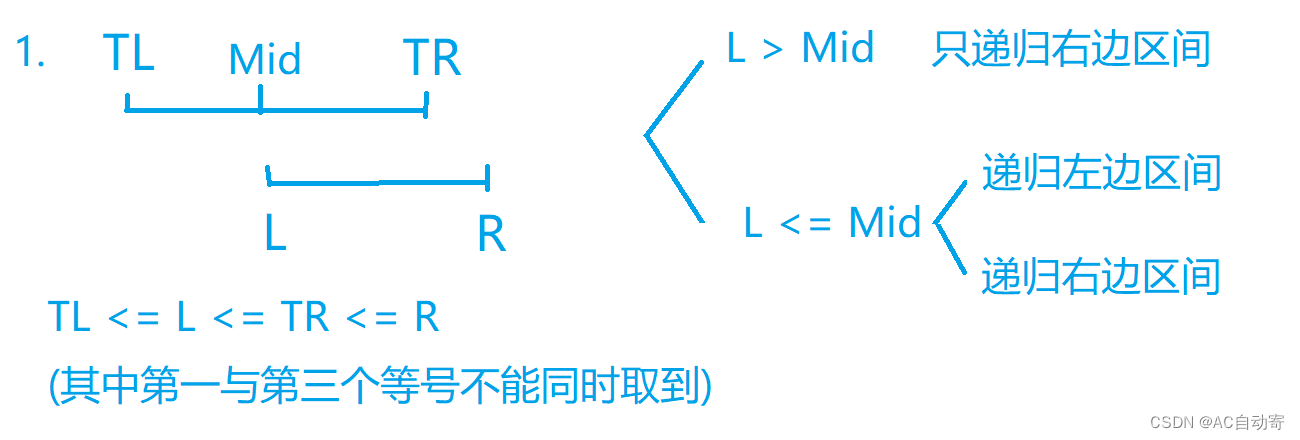
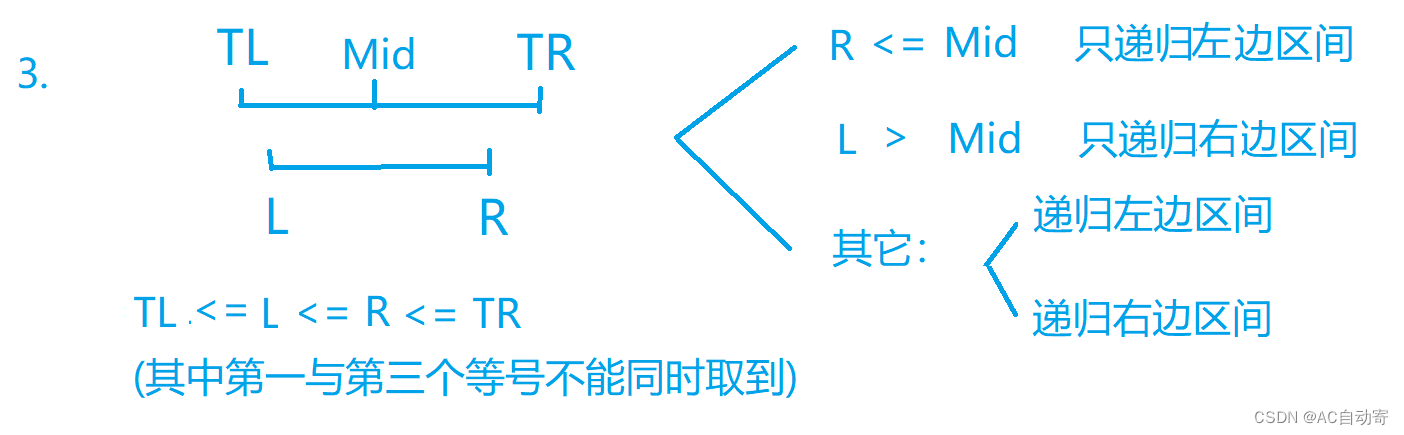
总结

1. 查询区间于树中区间有交集，则递归交集的部分：左边有交集递归左边，右边有交集递归右边

2. 一般只有两条链递归至叶子节点，时间复杂度为 $O(logN)$，但 $logN$ 的常数较大(比树状数组，st表等都大)

3. $[L,R]\cap [T_L,T_R]=\varnothing$
不存在此种情况！！！