【python】实现k-means

K-Means

（理论部分略）

步骤：

1. 选择初始化的k个样本作为初始聚类$C=C_1,...,C_k$
2. 针对数据集中每个样本$x_i$，计算它到k个聚类中心的距离，并将其分到距离最小的聚类中心所对应的类别
3. 针对每个类别$C_j$，重新计算它的聚类中心点$$C_j=\frac{1}{c_i}\sum _{x\in c_i}x$$
4. 重复

K值选取的方式

手肘法 ： 计算误差平方和（SSE），即所有样本的聚类误差
SSE：$$SSE=\sum _{i=1}^k\sum _{p\in C_i}|p-m_i{|}^2$$

$c_i$是第i簇，p为$c_i$的中样本点，$m_i$为$c_i$的质心，随着k的增大，样本划分更精细，每个簇的聚合程度会逐渐提高，因此SSE会减少，呈现下图：

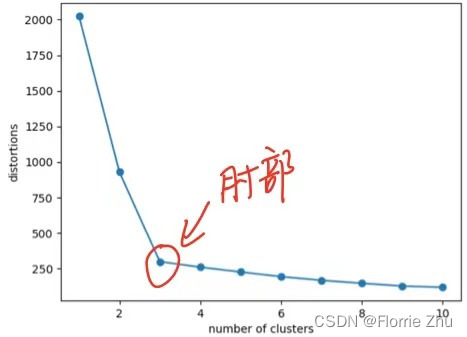
因此，可以按以下规律选择k值：

• k<真实聚类数，k$\uparrow$，SSE$\downarrow$
• k>真实聚类数，k$\downarrow$，SSE趋向于平缓

因此，一般取肘部时的k值。

实现代码

def classify(data, centers):
    '''
    聚类，计算数据和类别中心点聚类，与对应类别距离最短的为一类
    Args:
        data: 数据 ndarray(n,2)
        centers: 类别的中心点 ndarray(c,2)
    Returns: 新的类别(list)，新的距离(float)
    '''
    # 类别数
    clen = centers.shape[0]
    # 类的列表，装每个类有哪些数据
    classes = [ [] for i in range(clen)]

    # 距离
    sumDis = 0

    for i in range(data.shape[0]):
        per_data = data[i]
        # np.tile()将数据横向或纵向拷贝 -> [1,3] 纵向拷贝三份得到，[[1,3],[1,3],[1,3]]
        # 采用tile将数据拷贝clen份，然后在对应维度上进行相减，可以得到 当前坐标点与所有类别的距离
        diff = np.tile(per_data, (clen, 1)) - centers
        # ((x2-x1)^2+(y2-y1)^2) 距离平方求和
        sqDiff = diff**2
        sqDiff = sqDiff.sum(axis=1)

        # 对距离排序
        sortIdx = sqDiff.argsort()
        # 取距离最小的类别索引，把当前数据放入该类别
        classes[sortIdx[0]].append(list(per_data))

        # 记录最小距离
        sumDis += sqDiff[sortIdx[0]]

    return classes, sumDis


def updateCenters(classes):
    # 新的中心点
    new_centers = []
    
    for i in range(len(classes)):
        per_class = classes[i]  # list
        # 转ndarray
        per_class = np.array(per_class)
        center = per_class.sum(axis=0) / len(per_class)
        new_centers.append(center)
    
    return np.array(new_centers)
        


def kmeans(data, centers, sumDis):
    '''
    聚类
    Args:
        data:数据
        centers:类别中心点
        sumDis:距离总和

    Returns:

    '''
    # 聚类
    classes, new_sumDis = classify(data, centers)
    # 如果新的中心点不变，则结束
    if sumDis == new_sumDis:
        return
    # 更新中心点
    new_centers = updateCenters(classes)
    # 再聚类
    kmeans(data, new_centers, new_sumDis)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

优点

1. 容易理解，聚类效果不错，虽然是局部最优， 但往往局部最优就够了；
2. 处理大数据集的时候，该算法可以保证较好的伸缩性；
3. 当簇近似高斯分布的时候，效果非常不错；
4. 算法复杂度低。

缺点

1. K 值需要人为设定，不同 K 值得到的结果不一样；
2. 对初始的簇中心敏感，不同选取方式会得到不同结果；
3. 对异常值敏感；
4. 样本只能归为一类，不适合多分类任务；
5. 不适合太离散的分类、样本类别不平衡的分类、非凸形状的分类。