AVL树四种旋转的详细图解

什么是AVL树？AVL树是具有下下性质的搜索二叉树

1. 它的左右子树都是AVL树
2. 左右子树的高度差不超过1（-1、0、1）

 

如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在O(log(n)) ，搜索时间复杂度O(log(n) )。

AVL树节点的定义

template<class T>
class AVLTreeNode
{
private:
    AVLTreeNode<T>* pleft;
    AVLTreeNode<T>* pright;
    AVLTreeNode<T>* pParent;
    T _data;
    int _bf;
public:
    AVLTreeNode(const T& data)
        :_data(data)
        ,_bf(0)//平衡因子，用它来保持平衡
    {
        pleft=nullptr;
        pright=nullptr;
        pParent=nullptr;
    }
 
};

在插入新的节点后，夫节点的平衡因子需要更新，在插入之前其父亲的平衡因子有三种情况

-1，0，1.

1. 如果插入到父亲节点的左侧，只需要给父亲节点的平衡因子-1
2. 如果插入到父亲节点的右侧，只需要给父亲节点的平衡因子+1

 调整后的父亲的平衡因子有三种情况，分别为，0，±1，±2，

1. 如果父亲节点的平衡因子为0，则插入前父亲的节点的平衡因子为±1，此时满足条件，插入成功
2. 如果父亲节点的平衡因子为±1，则插入前父亲节点的平衡因子一定为0，插入后成±1，满足条件，插入成功
3. 如果父亲节点的平衡因子为±2，则平衡因子违反了平衡树的性质，需要对其进行旋转处理

接下来我们重点讨论你下怎么旋转的问题，有哪些条件需要旋转，怎么旋转

如图是需要右单旋

 

左单旋

 

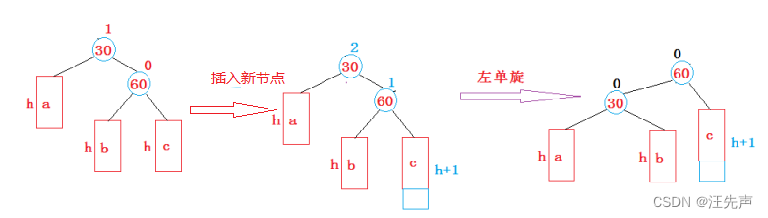
 左右单旋

右左单旋

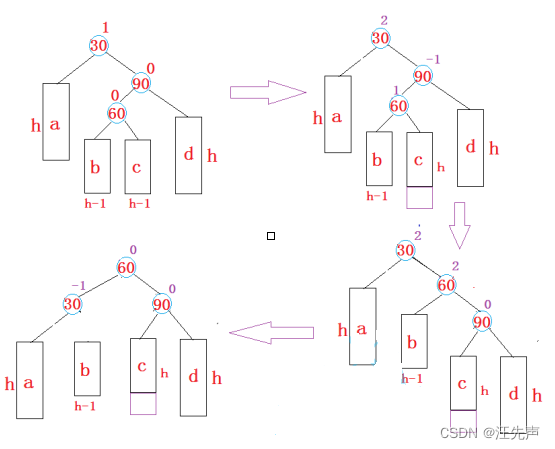
 总结：

假如以pParent为根的子树不平衡，即pPanrende平衡因子为2或者-2，分以下几种情况需要考虑

1、pParent的平衡因子为2时，说明pParent的右子树高，设pParent的右子树的根为psubR

1. 当psubR的平衡因子为1，则需要做左单旋
2. 当psubR的平衡因子为-1，则需要做右左单旋

 2. pParent的平衡因子为-2，说明pParent的左子树高，设pParent的左子树的根为pSubL

1. 当pSubL的平衡因子为-1是，执行右单旋
2. 当pSubL的平衡因子为1时，执行左右双旋

旋转完成后，原pParent为根的子树个高度降低，已经平衡，不需要再向上更新。