编辑距离1：

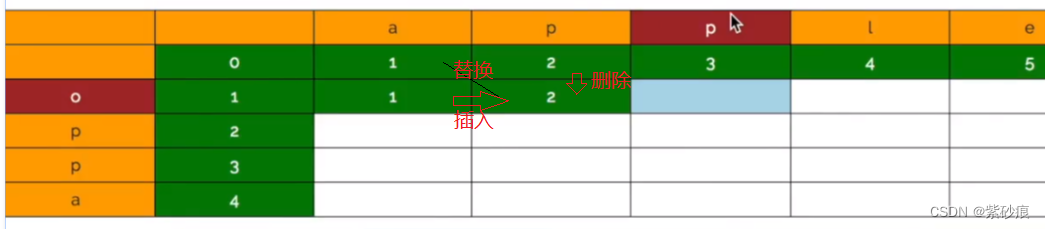
如果 word1[i] == word2[j], 那么直接是等于 word1[i-1]到 word2[j-1]的编辑距离

如果word1[i] ！= word2[j], 那么 从左上、左边、 上边，三个位置选出最小距离 ，然后再加上1，就是当前位置的编辑距离

#
# 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
#
# 
# @param str1 string字符串 
# @param str2 string字符串 
# @return int整型
#
class Solution:
    def editDistance(self , str1: str, str2: str) -> int:
        # write code here
        m = len(str1)
        n = len(str2)
        if m == 0 or n == 0:
            return max(m, n)
        dp = [[0 for j in range(n+1)] for i in range(m+1)]
        dp[0][0] = 0
        for i in range(1, m+1):
            dp[i][0] = i
        for j in range(1, n+1):
            dp[0][j] = j     
            
        for i in range(1, m+1):
            for j in range(1, n+1):
                if str1[i-1] == str2[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j], dp[i][j-1])) +1
        return  dp[-1][-1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

#
# 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
#
# min edit cost
# @param str1 string字符串 the string
# @param str2 string字符串 the string
# @param ic int整型 insert cost
# @param dc int整型 delete cost
# @param rc int整型 replace cost
# @return int整型
#
class Solution:
    def minEditCost(self , str1: str, str2: str, ic: int, dc: int, rc: int) -> int:
        # write code here
        m = len(str1)
        n = len(str2)
        if m == 0 or n == 0:
            return max(m, n)
        dp = [[0 for j in range(n+1)] for i in range(m+1)]
        dp[0][0] = 0
        for i in range(1, m+1):
            dp[i][0] = dc*i   # str1 变成空字符串， 删除操作
        for j in range(1, n+1):
            dp[0][j] = ic*j   # 空字符串变成 str2    插入操作
            
        # str1 -> str2 :
        # [i-1][j-1] -> [i][j]  替换操作
        # [i-1][j] -> [i][j]  删除操作
        # [i][j-1] -> [i][j]  插入操作 
        
        for i in range(1, m+1):
            for j in range(1, n+1):
                if str1[i-1] == str2[j-1]:
                    dp[i][j] = dp[i-1][j-1]
                else:
                    dp[i][j] = min(rc + dp[i-1][j-1], min(dp[i-1][j] + dc, dp[i][j-1]+ic)) 
                
        return  dp[-1][-1]
        
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39