-
矩阵分析与应用(20)
学习来源:《矩阵分析与应用》 张贤达 清华大学出版社
奇异值分解一、矩阵奇异值与矩阵的关系
矩阵的奇异值与矩阵的范数、行列式、条件数、特征值等有密切关系。
1. 奇异值与范数的关系
矩阵
 的谱范数等于
的谱范数等于  的最大奇异值,即
的最大奇异值,即
根据矩阵的奇异值分解定理,由于矩阵
 的 Frobenius 范数
的 Frobenius 范数  是酉不变的,即
是酉不变的,即
因此,有
![\left \| A \right \|_F=\left [ \sum_{i=1}^{m}\sum_{j=1}^{n}\left | a_{ij} \right |^2 \right ]^{\frac{1}{2}}](https://1000bd.com/contentImg/2022/08/11/085217010.gif)


也就是说,任何一个矩阵的 Frobenius 范数等于该矩阵所有非零奇异值平方和的正平方根。
2. 奇异值与行列式的关系
设
 是
是 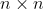 正方矩阵。由于酉矩阵的行列式的绝对值为 1 ,所以有
正方矩阵。由于酉矩阵的行列式的绝对值为 1 ,所以有
当所有的
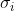 都不为零,则
都不为零,则  是非奇异的;当存在
是非奇异的;当存在 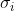 为零时,则
为零时,则  是奇异的。
是奇异的。对于一个
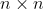 矩阵
矩阵  ,以下不等式均成立:
,以下不等式均成立:3. 奇异值与条件数的关系
对于一个
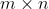 矩阵
矩阵  ,其条件数可以利用奇异值定义为
,其条件数可以利用奇异值定义为![cond(A)=\frac{\sigma_1}{\sigma_p},\qquad p=min\left \{ m,n \right \}]](https://1000bd.com/contentImg/2022/08/11/085226144.gif)
因为
 ,所以条件数是一个大于或等于 1 的正数。对于一个奇异矩阵来说,由于至少有一个奇异值
,所以条件数是一个大于或等于 1 的正数。对于一个奇异矩阵来说,由于至少有一个奇异值  ,因此奇异矩阵的条件数为无穷大;当一个矩阵
,因此奇异矩阵的条件数为无穷大;当一个矩阵  的条件数不是无穷大但很大时,称矩阵
的条件数不是无穷大但很大时,称矩阵  是接近奇异的。它的意思是,当矩阵
是接近奇异的。它的意思是,当矩阵  的条件数很大时,矩阵
的条件数很大时,矩阵  的行向量或列向量的线性相关性很强。
的行向量或列向量的线性相关性很强。对于方程
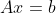 ,
, 的奇异值分解为
的奇异值分解为
即矩阵
 的最大和最小奇异值分别是矩阵
的最大和最小奇异值分别是矩阵  的最大和最小奇异值的平方,所以
的最大和最小奇异值的平方,所以![cond(A^HA)=\frac{\sigma_1^2}{\sigma_n^2}=\left [ cond(A) \right ]^2](https://1000bd.com/contentImg/2022/08/11/085231518.gif)
也就是说,矩阵
 的条件数是矩阵
的条件数是矩阵  的条件数的平方。
的条件数的平方。4. 奇异值与特征值的关系
设
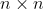 正方对称矩阵
正方对称矩阵  的特征值为
的特征值为  ,奇异值为
,奇异值为 ,则
,则 
二、奇异值的性质汇总
1. 奇异值服从的等式关系
1)矩阵
 和其复共轭转置矩阵
和其复共轭转置矩阵 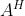 具有相同的奇异值。
具有相同的奇异值。2)矩阵
 的非零奇异值是
的非零奇异值是 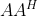 或
或  的非零特征值的正平方根。
的非零特征值的正平方根。3)
 是矩阵矩阵
是矩阵矩阵  的单奇异值,当且仅当
的单奇异值,当且仅当 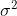 是
是 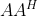 或
或  的单特征值。
的单特征值。4)若
 ,且
,且  是矩阵
是矩阵  的奇异值,则
的奇异值,则
5)矩阵行列式的绝对值等于矩阵奇异值的乘积,即

6)矩阵
 的谱范数等于
的谱范数等于  的最大奇异值,即
的最大奇异值,即  。
。7)若
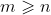 ,则对于矩阵
,则对于矩阵  ,有
,有

8)若
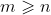 ,则对于矩阵
,则对于矩阵  ,有
,有

9)若
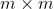 矩阵
矩阵  非奇异,则
非奇异,则
10)若
 是
是 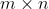 矩阵
矩阵  的奇异值分解,则
的奇异值分解,则  的 Moose-Penrose 逆矩阵
的 Moose-Penrose 逆矩阵
11)若
 是
是 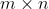 矩阵
矩阵  的非零奇异值(其中,
的非零奇异值(其中,  ),则矩阵
),则矩阵  具有
具有  个非零奇异值
个非零奇异值  和
和  个零奇异值。
个零奇异值。2. 奇异值服从的不等式关系
1)若
 和
和 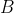 是
是 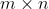 矩阵,则对于
矩阵,则对于  ,有
,有
特别地,当
 时,
时,  成立。
成立。2)对矩阵
 ,有
,有
3)若
 和
和 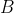 是
是 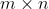 矩阵,则
矩阵,则![\sum_{j=1}^{p}\left [ \sigma_j(A+B)-\sigma_j(A) \right ]^2 \leqslant \sigma_{max}(A)+\sigma_{max}(B)](https://1000bd.com/contentImg/2022/08/11/085312410.gif)
4)若
![A_{m\times n}=[a_1,a_2,\cdots ,a_m]](https://1000bd.com/contentImg/2022/08/11/085313613.gif) 的奇异值
的奇异值  ,则
,则![\sum_{j=1}^{k}[\sigma_{m-k+j}(A)]^2\leqslant \sum_{j=1}^{k}a_j^Ha_j\leqslant \sum_{j=1}^{k}[\sigma_j(A)]^2,\quad k=1,2,\cdots ,m](https://1000bd.com/contentImg/2022/08/11/085315770.gif)
5)若
 ,且
,且  和
和 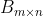 的奇异值排列为
的奇异值排列为  ,
, 和
和  ,则
,则
6)设
 矩阵
矩阵 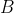 是去掉
是去掉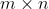 矩阵
矩阵  的任意一列得到的矩阵,且它们的奇异值都按照非降序排列,则
的任意一列得到的矩阵,且它们的奇异值都按照非降序排列,则
式中,
 。
。7)设
 矩阵
矩阵 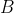 是去掉
是去掉 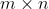 矩阵
矩阵  的任意一行的到的矩阵,且它们的奇异值按照非降序排列,则
的任意一行的到的矩阵,且它们的奇异值按照非降序排列,则
式中,
 。
。8)矩阵
 的最大奇异值满足不等式
的最大奇异值满足不等式![\sigma_{max }(A)\geqslant \left [ \frac{1}{n}tr(A^HA) \right ]^{\frac{1}{2}}](https://1000bd.com/contentImg/2022/08/11/085328442.gif)
-
相关阅读:
人工智能与设计的未来趋势,人工智能和建筑设计
MATLAB/Python编程:绘制一维和二维的分布直方图
Windows 内网渗透之攻击域控
linq to sql性能优化技巧
MHA高可用
nodejs+vue中小学课程辅导系统-计算机毕业设计
2022-06-28管理心得
戴尔大步进军经典量子计算混合模型
DJ12-2-2 算术运算指令
[AIGC] Maven 简介: Java 项目构建的利器
- 原文地址:https://blog.csdn.net/qq_40206924/article/details/126182157