第一章 矩阵与线性方程组（二十六）

1. Khatri-Rao积

如果$G$是$t\times u$矩阵，而$F$是$q\times u$矩阵，即$G$和$F$有相同的列数，则这两个矩阵的Khatri-Rao积记为$F\ast G$，并定义为
$$F\ast G=[f_1\otimes g_1,f_2\otimes g_2,\dots ,f_u\otimes g_u]$$

2. 广义Kronecker积

给定$N$个$m\times r$矩阵$A_i,i=1,2,\dots ,N$，它们组成矩阵组 { A } N \{A\}_N {A}N​该矩阵组与$N\times l$矩阵$B$的Kronecker积称为广义Kronecker积，定义为
{ A } N ⊗ B = [ A 1 ⊗ b 1 A 2 ⊗ b 2 ⋮ A N ⊗ b N ] \{A\}_N \otimes B=

{A}N​⊗B=⎣ ⎡​A1​⊗b1​A2​⊗b2​⋮AN​⊗bN​​⎦ ⎤​
式中，$b_i$是矩阵$B$的第$i$个行向量。
与两个矩阵的Kronecker积不同，广义Kronecker积是多个矩阵组成的矩阵组与另一个矩阵的Kronecker积。
显然，若每一个矩阵$A_i$相同，则广义Kronecker积简化为一般的左Kronecker积。

例
令

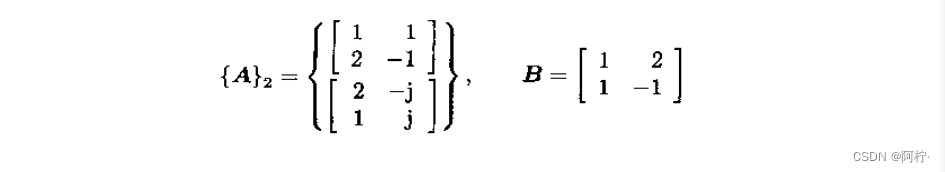
则广义Kronecker积为

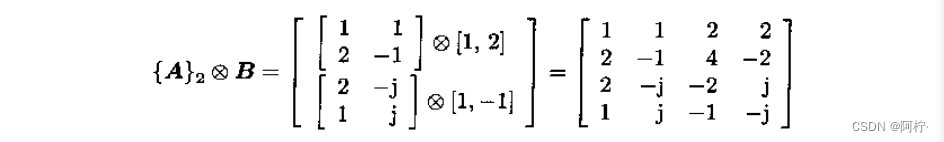
3. 广义Kronecker积的性质

(1)若 { A } \{A\} {A}的每一个矩阵为$m_1\times n_1$矩阵， { B } \{B\} {B}的每一个矩阵为$m_2\times n_2$矩阵，并且 { C } \{C\} {C}的每一个矩阵为$m_3\times n_3$矩阵，则
( { A } ⊗ { B } ) ⊗ { C } = { A } ⊗ ( { B } ⊗ { C } ) (\{A\}\otimes \{B\})\otimes \{C\}=\{A\}\otimes (\{B\}\otimes \{C\}) ({A}⊗{B})⊗{C}={A}⊗({B}⊗{C})
(2)广义Kronecker积与矩阵直和之间存在以下关系:
{ A } N ⊗ I N = ⨁ i = 1 N A i \{A\}_N \otimes I_N = \bigoplus_{i=1}^NA_i {A}N​⊗IN​=i=1⨁N​Ai​
(3)若
{ A } E = [ A 1 E A 2 E ⋮ A N E ] \{A\}E=

{A}E=⎣ ⎡​A1​EA2​E⋮AN​E​⎦ ⎤​
则
( { A } E ) ⊗ ( { B } F ) = ( { A } ⊗ { B } ) ( E ⊗ F ) (\{A\}E)\otimes (\{B\}F)=(\{A\}\otimes \{B\})(E\otimes F) ({A}E)⊗({B}F)=({A}⊗{B})(E⊗F)
(4)令 { A ( 0 ) } , { A ( 1 ) } , … , { A ( p − 1 ) } \{A^{(0)}\},\{A^{(1)}\},…,\{A^{(p-1)}\} {A(0)},{A(1)},…,{A(p−1)}为$p$个矩阵组，并且第$k$个矩阵组有$N_k=m^k$个矩阵，即 { A ( k ) } N k \{A^{(k)}\}_{N_k} {A(k)}Nk​​。定义
R = { A ( p − 1 ) } m p − 1 ⊗ { A ( p − 2 ) } m p − 2 ⊗ { A ( 1 ) } m ⊗ A ( 0 ) R=\{A^{(p-1)}\}_{mp-1} \otimes \{A^{(p-2)}\}_{mp-2} \otimes \{A^{(1)}\}_m \otimes A^{(0)} R={A(p−1)}mp−1​⊗{A(p−2)}mp−2​⊗{A(1)}m​⊗A(0)
则矩阵$R$具有稀疏矩阵分解形式
$$R=\prod _{k=0}^{p-1}[\underset{i=0}{\overset{m^{p-k-1}-1}{⨁}}(I_{n^k}\otimes A_i^{p-k-1})]$$
(5)若每一个矩阵$A_i^{(k)}$为酉(或者仿酉)矩阵，则$R$是酉(或者仿酉)炬阵。
(6)若$m=n$，使得$A_i^{(k)},i=0,1,\dots ,m^k-1,k=0,1,\dots ,p-1$均为正方矩阵，则
$$det(R)=\prod _{k=0}^{p-1}\prod _{i=0}^{m^k-1}[det(A_i^{(k)}){]}^{m^k}$$

4. 向量化函数、Kronecker 乘幂和Khatri-Rao积的性质

(1)矩阵之和的向量化
$$vec(A+B)=vec(A)+vec(B)$$
(2)转置矩阵的向量化
$$vec(A^T)=K_{pq}vec(A)$$
(3)两个矩阵$A_{m\times n},B_{n\times p}$的向量化
$$vec(AB)=(I_s\otimes A)vec(B)=(B^T\otimes I_p)vec(A)$$
$$=(B^T\otimes A)vec(I_q)$$
(4)三个矩阵$A_{m\times n},B_{n\times p},C_{p\times q}$的向量化
$$vec(ABC)=(C^T\otimes A)vec(B)$$
(5)矩阵的Kronecker乘幂
$$A^{[k+1]}=A\otimes A^{[k]}$$
(6)矩阵乘积的Kronecker乘幂
$$(AB{)}^{[k]}=A^{[k]}{B}^{[k]}$$
(7)三个矩阵乘积的迹
$$tr(ABC)=(vec(A){)}^T(I_p\otimes B)vec(C)$$
(8)四个矩阵乘积的迹
$$tr(ABCD)=(vec(D^T){)}^T(C^T\otimes A)vec(B)$$
$$=(vec(D){)}^T(A\otimes C^T)vec(B^T)$$
(9)矩阵内积的迹等于两个矩阵的向量化函数的内积，即
$$tr(A^{T}D)=(vec(A){)}^{T}vec(D)$$
(10)Khatri-Rao积的结合律
$$A\ast (D\ast F)=(A\ast D)\ast F$$
(11)Khatri-Rao积$A\ast B$与$B\ast A$之间的关系
$$A\ast B=K_{nn}(B\ast A)$$
(12) Kronecker 积与Khatri-Rao积的乘积
$$(A\otimes B)(F\ast G)=AF\ast BG$$

5.Kronecker积的应用

Kronecker积最直接的应用是求解矩阵方程组
$$AXB=C$$
式中，$A$和$X$分别是$m\times n$和$n\times p$矩阵，而$B$和$C$的维数分别是$p\times q$和$m\times q$。
利用向量化算符，定义$x=vec(X)$和$c=vec(C)$，则方程组可以用矩阵的Kronecker积改写为
$$(A\otimes B^T)x=c$$
一旦解向量$x$求出后，即可利用向量的矩阵化算符得到原矩阵方程组的解矩阵$X=unvec(x)$。

5.1 向量过程的累积量

考查观测过程$y(n)$，它是一个$p$维随机向量，即$y(n)=[y_1(n),y_2(n),\dots ,y_p(n){]}^T$。随机向量的累积量有两种不同的定义选择。

• 一种方式模仿概率论中的第二特征函数(又叫累积量生成函数)定义。
  令向量$w_i=w_{i1},w_{i2},\dots ,w_{ip}{]}^T,i=1,2,\dots ,k$和$y=[y^T(n),y^T(n+r_1),\dots ,y^T(n+T_{k_1})]$(现在$w_i$和$y$均为$pk$维向量)，并产生累积量生成函数$InEexp(j{w}_{i}y)$，再用该生成函数的Taylor级数展开系数定义随机向量$y$的高阶累积量。但是，这种定义最后的表达式太复杂，并且难于推导出其他很多有用的公式。
• 与上述定义方式不同，另外一种定义具有很多明显的优点。这种方式定义向量元素的互累积量，例如
  $$C_{y_i,y_j,y_l}(n;r_1,r_2)=E{y}_i(n)y_j(n+r_1)y_l(n+r_2)$$
  是$y_i(n),y_j(n)和y_l(n)$的三阶累积量。这样一种定义能更加方便地表示随机向量的$k$阶累积量，也有利于累积量之间的运算。

5.2 多信道BBR公式

除了使用状态空间模型外，随机向量过程$y(n)$也可视为一个线性多信道系统的输出，该系统的冲激响应矩阵为$H(n,k)$，输入为随机向量$e(n)$。具体地说，$y(n)$可表征为
$$y(n)=\sum _{k=-\infty }^{\infty }H(n,k)e(n)\text{\hspace{1em}(1)}$$
其中，$y(n)\in R^{n_y},e(n)\in R^{n_e}$和$H(n,k)\in R^{n_y}\times R^{n_e}$，且$X\times Y$表示非空集合$X$与$Y$的积集合，即$X\times Y=(x,y):x\in x\in X,y\in Y$。

假定$e(n)$与$e(m)，n\ne m$独立，即其累积量为多维Kronecker δ函数:
$$C_{ke}(n;{\tau }_1,\dots ,{\tau }_{k-1})=cume(n),e(n+{\tau }_1),\dots ,e(n+{\tau }_{k-1})$$
$$={{\rm Y}}_{ke}(n)\delta ({\tau }_l)\dots \delta {\tau }_{k-1})\text{\hspace{1em}(2)}$$
式中，输入累积量${{\rm Y}}_{ke}(n)$是一个有$n_e^k$元素的向量。

定理(多信道BBR公式)
对于由(1)式定义的线性向量过程$y(n)$，若输入满足(2)式，且冲激响应矩阵$H(n,k)$是绝对可和的，即
$$\sum _{n=0}^{\infty }\sum _{k=-\infty }^{\infty }|H(n,k)|<\infty$$
则输出向量过程的$k$阶累积量向量由BBR公式给出;并且当系统是时不变即 $H(n,k)=H(n-k)$以及${{\rm Y}}_{ke}(n)={{\rm Y}}_{ke}$时，
$$c_{ky}({\tau }_1,...,{\tau }_{k-1})=\sum _{i=-\infty }^{\infty }[H(i)\otimes H(i+{\tau }_1)\otimes ...\otimes H(i+{\tau }_{k-1})]{{\rm Y}}_{ke}$$
$$=\sum _{i=-\infty }^{\infty }[\underset{l=0}{\overset{l-1}{⨂}}H(i+{\tau }_l)]{{\rm Y}}_{ke},{\tau }_0=0$$
利用Kronecker积还容易推导出多信道ARMA过程的累积量与多信道AR参数之间的线性法方程-多信道修正Yule-Walker(MYW)方程，它是辨识多信道ARMA模型的关键方程。