目录

一、算法简介

1.排序思想

2.优化思路

二、算法实现

1.代码实现

2.测试用例即结果

三、性能分析

1.时间复杂度

2.空间复杂度

3.稳定性

---

一、算法简介

1.排序思想

选择排序的思想就是通过遍历无序序列，每次从无序序列中选出最小（或最大）的元素，将其放到依次放到序列的起始（或末尾）位置，直到全部待排序的元素排序完成。

流程演示：

每次从待排序序列中选取最大元素，将其交换到待排序序列末尾，若最大元素本身就在末尾则不需要交换；待排序序列长度减一。经过n-1趟选择即可完成排序。

2.优化思路

在每次遍历待排序序列选取元素时，我们可以同时选取最大和最小两个元素，然后分别将其放到序列末尾和起始位置即可，这样每趟遍历我们可以一次性排好两个元素，从而提高算法效率。

注意：

采用此思路实现时需注意，当最小元素恰好在序列的最大元素待放入位置时，因为对最大元素进行放入后会改变最小元素位置，所有需要提前改变最小元素的标记位置为最大元素交换前的位置。

示例：

二、算法实现

1.代码实现

#include
using namespace std;
 
void ArryPrint(int* arr, int size) {//数组打印
	for (int i = 0; i < size; i++) {
		cout << arr[i] << ' ';
	}
}
 
void SelectSort(int* arr, int size) {//直接选择排序
	for (int i = 0; i < size - 1; i++) {//n-1趟排序，最后一个元素不需要再排序
		int maxPos = 0;
		for (int j = 0; j < size - i; j++) {//寻找待排序序列内最大元素的下标
			if (arr[j] > arr[maxPos]) {
				maxPos = j;
			}
		}
		if (maxPos != size - i - 1) {//若最大元素不在序列末尾，则交换到末尾
			swap(arr[size - i - 1],arr[maxPos]);
		}
	}
}
 
void SelectSortOP(int* arr, int size) {//直接选择排序优化版
	int begin = 0;//标记待排序序列区间
	int end = size - 1;
	while (begin < end) {//至少还有2个元素
		int minPos = begin;
		int maxPos = begin;
		int index = begin + 1;
		while (index <= end) {//选取待排序序列最大和最小元素
			if (arr[index] > arr[maxPos]) {
				maxPos = index;
			}
			if (arr[index] < arr[minPos]) {
				minPos = index;
			}
			index++;
		}
		if (minPos == end) {//若最小元素恰好在末尾，提前改变其标记位置
			minPos = maxPos;
		}
		if (maxPos != end) {//将最大元素交换到末尾
			swap(arr[maxPos], arr[end]);
		}
		if (minPos != begin) {//将最小元素交换到起始
			swap(arr[begin], arr[minPos]);
		}
		end--;
		begin++;
	}
}
 
void Test() {
	int arr[] = { 5,8,4,7,1,9,3,2,0 };
	int size = sizeof(arr) / sizeof(arr[0]);
 
	cout << "排序前：";
	ArryPrint(arr, size);
	//SelectSort(arr, size);
	SelectSortOP(arr, size);
	cout << endl << "排序后：";
	ArryPrint(arr, size);
}
 
int main() {
	Test();
	return 0;
}

2.测试用例即结果

用例：int arr[] = { 5,8,4,7,1,9,3,2,0 }

普通版本测试结果：

优化版本测试结果：

 

三、性能分析

1.时间复杂度

 O()：

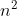根据算法的实现思想和代码实现可知，直接选择排序内循环中代码的执行次数固定为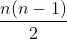次，与待排序序列的初始状态无关，时间复杂度计算只关心其最终量级，所以直接选择排序算法的时间复杂度为O()。

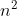2.空间复杂度

O(1)：

因为算法实现中除了用于标记元素位置的临时变量外，没有借助额外的复制空间，所以直接选择排序的空间复杂度为O(1)。

3.稳定性

不稳定：

​因为算法实现中，每次遍历待排序序列选取元素后，是将其放入到序列的最后位置，所以序列中相同元素位置靠前的先放入到序列末尾，靠后的元素后放入末尾，改变了其相对位置，所以直接选择排序不稳定。

活动地址：CSDN21天学习挑战赛

​