-
今天就跟你们聊聊缓存穿透吧

小编之前在面试字节提前批的时候,二面的面试官就问过 Redis 缓存穿透的问题,下面让我们一起深度还原一下陌溪当初的面试场景吧~
面试官:你的蘑菇博客项目用到了 Redis ?
小编:主要是为了缓解数据库压力,将首页的一些热门文章信息储存在 Redis 中。
面试官:好,那你知道什么是缓存穿透么?
小编:那我以蘑菇博客的场景来聊聊什么是缓存穿透。
什么是缓存穿透?
举个蘑菇博客中的案例来说,现在有一个 博客详情页 ,详情页中的内容是存储在 Redis 中的,通过博客的 uid 进行获取,正常的情况是:用户进入博客详情页,传递 uid 获取 Redis 中缓存的文章详情,如果有内容就直接访问,如果缓存为空,那么需要访问数据库,然后从数据库中查询我们的博客详情后,再存储到 Redis 中,最后把数据返回给我们的页面。
但是可能存在一些 非法用户 ,会通过不合法的 uid 去请求博客后台,首先 redis 的缓存没有命中该 key ,那么就会去请求数据库,这样大量非法的请求直接打在数据库中,可能会导致数据库直接 宕机 ,无法对外提供服务,这就是我们所说的缓存穿透问题。
面试官: OK ,那来谈谈蘑菇是怎么解决 缓存穿透 的?
小编(内心):糟糕,蘑菇博客中我并没有去解决缓存穿透问题,要是直接说没有解决,岂不是 回家等通知 了?
小编:针对上面出现的情况,我们有一种简单的解决方法就是,在数据库没有查询该条数据的时候,我们让该 key 缓存一个 空数据,这样用户再次以该 key 请求后台的时候,会直接返回 null ,避免了再次请求数据库。
面试官:好的,但是如果非法用户使用不同的 key 去请求后台时,那这样还是每次都不会命中缓存,都会查询数据库,针对这种情况,你有什么解决方法呢?
小编(内心):这面试连环炮有些遭不住,还好之前看八股文的时候,有看到过布隆过滤器,这会刚好可以说了。
小编:这种情况,我会使用布隆过滤器来解决这个问题~
什么是布隆过滤器?
布隆过滤器的巨大作用 ,就是能够迅速判断一个元素是否存在一个集合中。因此它有如下几个使用场景
-
网站爬虫对 URL 的去重,避免爬取相同的 URL 。
-
反垃圾邮件,从数十亿个垃圾邮件列表中判断某邮箱是否是垃圾邮件(同理,垃圾短信)
-
缓存穿透,将所有可能的数据缓存放到布隆过滤器中,当黑客访问不存在的缓存时,迅速返回避免缓存以及 DB 挂掉。
布隆过滤器其内部维护了一个全为 0 的 bit 数组,需要说明的是,布隆过滤器有一个误判的概念,误判率越低,则数组越长,所占空间越大。误判率越高则数组越小,所占的空间多少。
假设,根据误判率,我们生成一个 10 位的 bit 数组,以及 2 个 hash 函数 f1 和 f2 ,如下图所示:生成的数组的位数 和 hash 函数的数量。这里我们不用去关心如何生成的,因为有数学论文进行验证。

然后我们输入一个集合,集合中包含 N1 和 N2 ,我们通过计算 f1(N1) = 2 , f2(N1) = 5 ,则将数组下标为 2 和下标为 5 的位置设置成 1 ,就得到了下图。

同理,我们再次进行计算 N2的值, f1(N2) = 3,f2(N2) = 6。得到如下所示的图
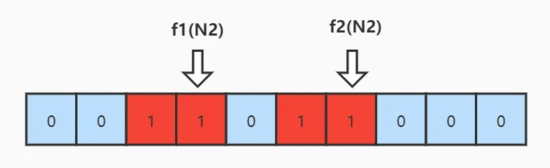
这个时候,假设我们有第三个数 N3 过来了,需要判断 N3 是否在集合 [N1,N2] 中,需要做的操作就是,使用 f1 和 f2 计算出数组中的地址
-
若值恰巧都位于上图的红色位置,我们认为 N3在集合 [N1,N2] 中
-
若值有一个不位于上图的红色部分,我们认为N3不在集合 [N1,N2] 中
这就是布隆过滤器的计算原理。
如何使用布隆过滤器
在 Java 中使用布隆过滤器,首先需要引入依赖,布隆过滤器拥有 Google 提供的一个开箱即用的组件,来帮助实现布隆过滤器。其实布隆过滤器的核心思想其实并不难,难的是在于如何设计随机映射函数,到底映射几次,二进制向量设置多少比较合适。
com.google.guava guava 22.0 - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
然后编写代码,测试某元素是否存在于百万元素集合中
private static int size = 1000000;//预计要插入多少数据 private static double fpp = 0.01;//期望的误判率 private static BloomFilterbloomFilter = BloomFilter.create(Funnels.integerFunnel(), size, fpp); public static void main(String[] args) { //插入数据 for (int i = 0; i < 1000000; i++) { bloomFilter.put(i); } int count = 0; for (int i = 1000000; i < 2000000; i++) { if (bloomFilter.mightContain(i)) { count++; System.out.println(i + "误判了"); } } System.out.println("总共的误判数:" + count); } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
代码分析
上面的代码中,我们创建了一个布隆过滤器,其中有两个重要的参数,分别是要预计插入的数据和我们所期望的误判率,误判率率不能为 0 。
首先向布隆过滤器中插入 0 ~ 100万 条数据,然后在用 100万 ~ 200 万的数据进行测试
最后输出结果,查看一下误判率
1999501误判了 1999567误判了 1999640误判了 1999697误判了 1999827误判了 1999942误判了 总共的误判数:10314
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
现在有 100万 不存在的数据,误判了 10314 次,通过计算可以得出 误判率
10314 / 1000000 = 0.010314
- 1
- 2
和之前定义的误判率为 0.01 相差无几,这也说明了布隆过滤器在处理 Redis 缓存穿透问题上,也具有比较好的表现。
-
-
相关阅读:
04. 人工智能核心基础 - 导论(3)
Leetcode33. Search in Rotated Sorted Array | Binary Search
F - Decreasing Heights
KingbaseESV8R6 snapshot too old的配置和测试
SmartBeta
大数据开发之Sqoop详细介绍
Nginx的Map模块
qlib格式的可转债数据:正股价,转股价的整合
UOS 开启 VisualStudio 远程调试 .NET 应用之旅
推荐几款比较使用的idea插件
- 原文地址:https://blog.csdn.net/m0_57042151/article/details/126171447
