-
吴恩达深度学习deeplearning.ai——第一门课:神经网络与深度学习——第二节:神经网络基础(下)
2.11 向量化(Vectorization)
向量化是非常基础的去除代码中for循环的技术,在深度学习安全领域、深度学习实践中,你会经常发现自己训练大数据集,因为深度学习算法处理大数据集效果很棒,所以你的代码运行速度非常重要,否则如果在大数据集上,你的代码可能花费很长时间去运行,你将要等待非常长的时间去得到结果。所以在深度学习领域,运行向量化是一个关键的技巧,让我们举个例子说明什么是向量化。
在逻辑回归中你需要去计算 z = w T x + b z={{w}^{T}}x+b z=wTx+b, w w w、 x x x都是列向量。如果你有很多的特征那么就会有一个非常大的向量,所以 w ∈ R n x w\in {{\mathbb{R}}^{{{n}{x}}}} w∈Rnx , x ∈ R n x x\in{{\mathbb{R}}^{{{n}{x}}}} x∈Rnx,所以如果你想使用非向量化方法去计算 w T x {{w}^{T}}x wTx,你需要用如下方式(python)
z=0 for i in range(n_x): z += w[i]*x[i] z += b- 1
- 2
- 3
- 4
这是一个非向量化的实现,你会发现这真的很慢,作为一个对比,向量化实现将会非常直接计算 w T x {{w}^{T}}x wTx,代码如下:
z=np.dot(w,x)+b- 1
这是向量化计算 w T x {{w}^{T}}x wTx的方法,你将会发现这个非常快
让我们用一个小例子说明一下,在我的我将会写一些代码(以下为教授在他的Jupyter notebook上写的Python代码,)
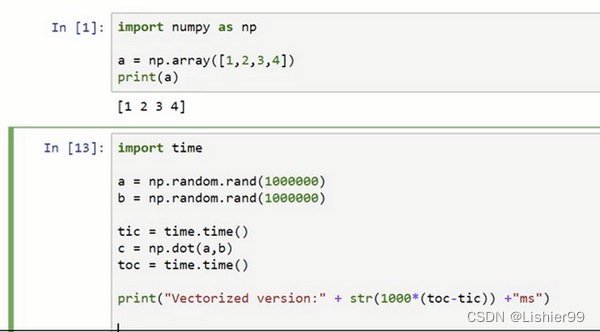
import numpy as np #导入numpy库 a = np.array([1,2,3,4]) #创建一个数据a print(a) # [1 2 3 4] import time #导入时间库 a = np.random.rand(1000000) b = np.random.rand(1000000) #通过round随机得到两个一百万维度的数组 tic = time.time() #现在测量一下当前时间 #向量化的版本 c = np.dot(a,b) toc = time.time() print("Vectorized version:" + str(1000*(toc-tic)) +"ms") #打印一下向量化的版本的时间 #继续增加非向量化的版本 c = 0 tic = time.time() for i in range(1000000): c += a[i]*b[i] toc = time.time() print(c) print("For loop:" + str(1000*(toc-tic)) + "ms")#打印for循环的版本的时间- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
返回值见图。
在两个方法中,向量化和非向量化计算了相同的值,如你所见,向量化版本花费了1.5毫秒,非向量化版本的for循环花费了大约几乎500毫秒,非向量化版本多花费了300倍时间。所以在这个例子中,仅仅是向量化你的代码,就会运行300倍快。这意味着如果向量化方法需要花费一分钟去运行的数据,for循环将会花费5个小时去运行。
一句话总结,和for循环相比,向量化可以快速得到结果。
你可能听过很多类似如下的话,“大规模的深度学习使用了GPU或者图像处理单元实现”,但是我做的所有的案例都是在jupyter notebook上面实现,这里只有CPU处理,CPU和GPU都有并行化的指令,叫做SIMD指令,这个代表了一个单独指令多维数据,它的基础意义是:如果你使用了built-in函数(像np.function)或者并不要求你实现循环的函数,它可以让python的充分利用并行化计算(而不是循环)。事实上,GPU更加擅长SIMD计算,即使CPU事实上也不是太差。接下来的视频中,你将看到向量化怎么能够加速你的代码,总而言之,无论什么时候,避免使用明确的for循环。
以下代码及运行结果截图:
2.12 向量化的更多例子(More Examples of Vectorization)
从上节中,你知道了怎样通过numpy内置函数和避开显式的循环(loop)的方式进行向量化,从而有效提高代码速度。
经验提醒我,当我们在写神经网络程序时,或者在写逻辑(logistic)回归,或者其他神经网络模型时,应该避免写循环(loop)语句。虽然有时写循环(loop)是不可避免的,但是我们可以使用比如numpy的内置函数或者其他办法去计算,程序效率总是快于循环(loop)。
让我们看另外一个例子。如果你想计算向量 u = A v u = Av u=Av,这时矩阵乘法定义为,矩阵乘法的定义就是: u i = ∑ i ∑ j A ij v i u_{i} =\sum\limits_{i}^{}\sum\limits_{j}^{}{A_{\text{ij}}v_{i}} ui=i∑j∑Aijvi,这取决于你怎么定义 u i u_{i} ui值。
- 同样使用非向量化实现, u = n p . z e r o s ( n , 1 ) u=np.zeros(n,1) u=np.zeros(n,1), 并且通过两层循环 f o r ( i ) : f o r ( j ) : for(i):for(j): for(i):for(j):,得到 u [ i ] = u [ i ] + A [ i ] [ j ] ∗ v [ j ] u[i]=u[i]+A[i][j]*v[j] u[i]=u[i]+A[i][j]∗v[j] 。现在就有了 i i i 和 的两层循环,这就是非向量化。
- 向量化方式就可以用 u = n p . d o t ( A , v ) u=np.dot(A,v) u=np.dot(A,v),右边这种向量化实现方式,消除了两层循环使得代码运行速度更快。

下面通过另一个例子继续了解向量化。如果你已经有一个向量 v v v,并且想要对向量 v v v的每个元素做指数操作,得到向量 u u u等于 e e e的 v 1 v_1 v1, e e e的 v 2 v_2 v2,一直到 e e e的 v n v_n vn次方。这里是非向量化的实现方式,首先你初始化了向量 u = n p . z e r o s ( n , 1 ) u=np.zeros(n,1) u=np.zeros(n,1),并且通过循环依次计算每个元素。但事实证明可以通过python的numpy内置函数,帮助你计算这样的单个函数。所以我会引入
import numpy as np,执行 u = n p . z e r o s ( n , 1 ) u=np.zeros(n,1) u=np.zeros(n,1) 命令。注意到,在之前有循环的代码中,这里仅用了一行代码,向量 v v v作为输入, u u u作为输出。你已经知道为什么需要循环,并且通过右边代码实现,效率会明显的快于循环方式。事实上,numpy库有很多向量函数。比如
u=np.log是计算对数函数( l o g log log)、np.abs()计算数据的绝对值、np.maximum(v, 0)按元素计算 v v v中每个元素和和0相比的最大值,v**2代表获得元素 每个值的平方、1/v获取 v v v 中每个元素的倒数等等。所以当你想写循环时候,检查numpy是否存在类似的内置函数,从而避免使用循环(loop)方式。
那么,将刚才所学到的内容,运用在逻辑回归的梯度下降上,看看我们是否能简化两个计算过程中的某一步。以下我们逻辑回归的求导代码,有两层循环。在这例子我们有 n n n个特征值。如果你有超过两个特征时,需要循环 、 d w 2 dw_2 dw2 、 d w 3 dw_3 dw3 等等(图中是只有两个特征,实际上如果多个特征,有一个循环像绿色笔记那样,遍历 j = 1 , 2 , . . . , n x j = 1,2,...,n_x j=1,2,...,nx)。所以 j j j 的实际值是1、2 和 n x n_x nx,就是你想要更新的值。所以我们想要消除第二循环
那么在第一行,这样我们就不用初始化 d w 1 = 0 , d w 2 = 0 dw_1 = 0,dw_2 = 0 dw1=0,dw2=0 , 我们直接把所有 d w dw dw向量都初始化为0,即定义了一个 x x x行的一维向量,再用 u = n p . z e r o s ( n ( x ) , 1 ) u=np.zeros(n(x),1) u=np.zeros(n(x),1)初始化这个向量(每一行就是一个 d w dw dw) 。从而替代循环。我们仅仅使用了一个向量操作 d w = d w + x ( i ) d z ( i ) dw = dw + x^{(i)}dz^{(i)} dw=dw+x(i)dz(i)就能代替原本循环更新 。最后,我们得到 d w = d w / m dw = dw / m dw=dw/m 。现在我们通过将两层循环转成一层循环,我们仍然还有这个循环训练样本。
原操作:

向量化:

希望这个视频给了你一点向量化感觉,减少一层循环使你代码更快,但事实证明我们能做得更好。所以在下一节,我们将进一步的讲解逻辑回归,你将会看到更好的监督学习结果。在训练中不需要使用任何 for 循环,你也可以写出代码去运行整个训练集。到此为止一切都好,让我们看下一个视频。
2.13 向量化逻辑回归(Vectorizing Logistic Regression)
我们已经讨论过向量化是如何显著加速你的代码,在本节中我们将讨论如何实现逻辑回归的向量化计算。这样就能处理整个数据集,甚至不会用一个明确的for循环就能实现对于整个数据集梯度下降算法的优化,并且当我们后面谈到神经网络时同样也不会用到一个明确的 for 循环。
首先我们回顾一下逻辑回归的前向传播步骤。如果你有 m m m 个训练样本,然后对第一个样本进行预测,使用这个公式 z ( 1 ) = w T x ( 1 ) + b z^{(1)}=w^{T}x^{(1)}+b z(1)=wTx(1)+b 。然后计算激活函数 a ( 1 ) = σ ( z ( 1 ) ) a^{(1)}=\sigma (z^{(1)}) a(1)=σ(z(1)) ,计算第一个样本的预测值 y y y 。
然后对第二个样本进行预测,你需要计算 z ( 2 ) = w T x ( 2 ) + b z^{(2)}=w^{T}x^{(2)}+b z(2)=wTx(2)+b , a ( 2 ) = σ ( z ( 2 ) ) a^{(2)}=\sigma (z^{(2)}) a(2)=σ(z(2)) 。然后对第三个样本进行预测,你需要计算 z ( 3 ) = w T x ( 3 ) + b z^{(3)}=w^{T}x^{(3)}+b z(3)=wTx(3)+b , a ( 3 ) = σ ( z ( 3 ) ) a^{(3)}=\sigma (z^{(3)}) a(3)=σ(z(3)) ,依次类推。如果你有 m m m 个训练样本,你可能需要这样做 m m m 次。可以看出,为了完成前向传播步骤,即对我们的 m m m 个样本都计算出预测值。有一个办法可以并且不需要任何一个明确的for循环。让我们来看一下你该怎样做。
首先,回忆一下我们曾经定义了一个矩阵 X X X 作为你的训练输入,(如下图中蓝色 X X X )像这样在不同的列中堆积在一起。这是一个 n x n_x nx 行 m m m 列的矩阵。我现在将它写为Python numpy的形式(即每一列都是一个样品,每一行都是某个样品的某个特征值)
( n x , m ) (n_{x},m) (nx,m)
这只是表示 X X X 是一个 n x n_x nx 乘以 m m m 的矩阵 R n x × m R^{n_x \times m} Rnx×m。

现在我首先想做的是告诉你该如何在一个步骤中计算 z 1 z_1 z1、 z 2 z_2 z2 、 z 3 z_3 z3 等等。实际上,只用了一行代码。所以,我打算先构建一个 1 × m 1\times m 1×m 的矩阵,实际上它是一个行向量,同时我准备计算 z ( 1 ) z^{(1)} z(1), z ( 2 ) z^{(2)} z(2) ……一直到 z ( m ) z^{(m)} z(m) ,所有值都是在同一时间内完成。结果发现它可以表达为 w w w 的转置乘以大写矩阵 x x x 然后加上向量 [ b b . . . b ] [b b...b] [bb...b] , ( [ z ( 1 ) z ( 2 ) . . . z ( m ) ] = w T + [ b b . . . b ] ) ([z^{(1)} z^{(2)}...z^{(m)}]=w^{T}+[bb...b]) ([z(1)z(2)...z(m)]=wT+[bb...b]) 。 [ b b . . . b ] [b b...b] [bb...b] 是一个 1 × m 1\times m 1×m 的向量或者 1 × m 1\times m 1×m 的矩阵或者是一个 m m m 维的行向量。所以希望你熟悉矩阵乘法,你会发现的 w w w 转置乘以 x ( 1 ) x^{(1)} x(1) , x ( 2 ) x^{(2)} x(2) 一直到 x ( m ) x^{(m)} x(m) 。所以 w w w 转置可以是一个行向量。所以第一项 w T X w^{T}X wTX 将计算 w w w 的转置乘以 x ( 1 ) x^{(1)} x(1), w w w 转置乘以 x ( 2 ) x^{(2)} x(2) 等等。然后我们加上第二项 [ b b . . . b ] [b b...b] [bb...b] ,你最终将 b b b 加到了每个元素上。所以你最终得到了另一个 1 × m 1\times m 1×m 的向量。
[ z ( 1 ) z ( 2 ) . . . z ( m ) ] = w T X + [ b b . . . b ] = [ w T x ( 1 ) + b , w T x ( 2 ) + b . . . w T x ( m ) + b ] [z^{(1)} z^{(2)}...z^{(m)}]=w^{T}X+[b b...b]=[w^{T}x^{(1)}+b,w^{T}x^{(2)}+b...w^{T}x^{(m)}+b] [z(1)z(2)...z(m)]=wTX+[bb...b]=[wTx(1)+b,wTx(2)+b...wTx(m)+b] 。
w T x ( 1 ) + b w^{T}x^{(1)}+b wTx(1)+b 这是第一个元素, w T x ( 2 ) + b w^{T}x^{(2)}+b wTx(2)+b 这是第二个元素, w T x ( m ) + b w^{T}x^{(m)}+b wTx(m)+b 这是第 m m m 个元素。
如果你参照上面的定义,第一个元素恰好是 z ( 1 ) z^{(1)} z(1) 的定义,第二个元素恰好是 z ( 2 ) z^{(2)} z(2) 的定义,等等。所以,因为 X X X是一次获得的,当你得到你的训练样本,一个一个横向堆积起来,这里我将 [ z ( 1 ) z ( 2 ) . . . z ( m ) ] [z^{(1)} z^{(2)} ... z^{(m)}] [z(1)z(2)...z(m)] 定义为大写的 Z Z Z ,你用小写 z z z 表示并将它们横向排在一起。所以当你将不同训练样本对应的小写 x x x 横向堆积在一起时得到大写变量 X X X 并且将小写变量也用相同方法处理,将它们横向堆积起来,你就得到大写变量 Z Z Z 。结果发现,为了计算 W T X + [ b b . . . b ] W^{T}X+[b b ... b] WTX+[bb...b] ,numpy命令是 Z = n p . d o t ( w . T , X ) + b Z=np.dot(w.T,X)+b Z=np.dot(w.T,X)+b。**这里在Python中有一个巧妙的地方,这里 b b b 是一个实数,或者你可以说是一个 1 × 1 1\times 1 1×1 矩阵,只是一个普通的实数。但是当你将这个向量加上这个实数时,Python自动把这个实数 b b b 扩展成一个 1 × m 1\times m 1×m 的行向量。所以这种情况下的操作似乎有点不可思议,它在Python中被称作广播(brosdcasting),目前你不用对此感到顾虑,我们将在下一个视频中进行进一步的讲解。话说回来它只用一行代码,用这一行代码,你可以计算大写的 Z Z Z,而大写 Z Z Z 是一个包含所有小写 z ( 1 ) z^{(1)} z(1) 到 z ( m ) z^{(m)} z(m) 的 1 × m 1\times m 1×m 的矩阵。这就是 Z Z Z 的内容,关于变量 a a a 又是如何呢?
我们接下来要做的就是找到一个同时计算 [ a ( 1 ) a ( 2 ) . . . a ( m ) ] [a^{(1)} a^{(2)} ... a^{(m)}] [a(1)a(2)...a(m)] 的方法。就像把小写 x x x 堆积起来得到大写 X X X 和横向堆积小写 z z z 得到大写 Z Z Z 一样,堆积小写变量 a a a 将形成一个新的变量,我们将它定义为大写 A A A。在编程作业中,你将看到怎样用一个向量在sigmoid函数中进行计算。所以sigmoid函数中输入大写 Z Z Z 作为变量并且非常高效地输出大写 A A A。你将在编程作业中看到它的细节。
总结一下,在这张幻灯片中我们已经看到,不需要for循环,利用 m m m 个训练样本一次性计算出小写 z z z 和小写 a a a,用一行代码即可完成。
Z = np.dot(w.T,X) + b- 1
这一行代码: A = [ a ( 1 ) a ( 2 ) . . . a ( m ) ] = σ ( Z ) A=[a^{(1)} a^{(2)} ... a^{(m)}]=\sigma (Z) A=[a(1)a(2)...a(m)]=σ(Z) ,通过恰当地运用 σ \sigma σ一次性计算所有 a a a。这就是在同一时间内你如何完成一个所有 m m m 个训练样本的前向传播向量化计算。
概括一下,你刚刚看到如何利用向量化在同一时间内高效地计算所有的激活函数的所有 a a a值。接下来,可以证明,你也可以利用向量化高效地计算反向传播并以此来计算梯度。让我们在下一个视频中看该如何实现。
2.14 向量化 logistic 回归的梯度输出(Vectorizing Logistic Regression’s Gradient)
注:本节中大写字母代表向量,小写字母代表元素
如何向量化计算的同时,对整个训练集预测结果 a a a,这是我们之前已经讨论过的内容。在本次视频中我们将学习如何向量化地计算 m m m个训练数据的梯度,本次视频的重点是如何同时计算 m m m 个数据的梯度,并且实现一个非常高效的逻辑回归算法(Logistic Regression)。
之前我们在讲梯度计算的时候,列举过几个例子, d z ( 1 ) = a ( 1 ) − y ( 1 ) dz^{(1)}=a^{(1)}-y^{(1)} dz(1)=a(1)−y(1), d z ( 2 ) = a ( 2 ) − y ( 2 ) dz^{(2)}=a^{(2)}-y^{(2)} dz(2)=a(2)−y(2) ……等等一系列类似公式。现在,对 m m m个训练数据做同样的运算,我们可以定义一个新的变量 d Z = [ d z ( 1 ) , d z ( 2 ) . . . d z ( m ) ] dZ=[dz^{(1)} ,dz^{(2)} ... dz^{(m)}] dZ=[dz(1),dz(2)...dz(m)] ,所有的 d z dz dz 变量横向排列,因此, d Z dZ dZ 是一个 1 × m 1\times m 1×m 的矩阵,或者说,一个 m m m 维行向量。在之前的幻灯片中,我们已经知道如何计算 A A A,即 [ a ( 1 ) , a ( 2 ) . . . a ( m ) ] [a^{(1)},a^{(2)} ... a^{(m)}] [a(1),a(2)...a(m)],我们需要找到这样的一个行向量 Y = [ y ( 1 ) , y ( 2 ) , . . . , y ( m ) ] Y=[y^{(1)}, y^{(2)} ,... ,y^{(m)}] Y=[y(1),y(2),...,y(m)] ,由此,我们可以这样计算 d Z = A − Y = [ a ( 1 ) − y ( 1 ) , a ( 2 ) − y ( 2 ) , . . . , a ( m ) − y ( m ) ] dZ=A-Y=[a^{(1)}-y^{(1)}, a^{(2)}-y^{(2)}, ... ,a^{(m)}-y^{(m)}] dZ=A−Y=[a(1)−y(1),a(2)−y(2),...,a(m)−y(m)],不难发现第一个元素就是 d z ( 1 ) dz^{(1)} dz(1),第二个元素就是 d z ( 2 ) dz^{(2)} dz(2) ……所以我们现在仅需一行代码,就可以同时完成这所有的计算。
在之前的实现中,我们已经去掉了一个for循环,但我们仍有一个遍历训练集的循环,如下所示:
d w = 0 dw=0 dw=0
d w + = x ( 1 ) ∗ d z ( 1 ) dw + = x^{(1)}*{dz}^{(1)} dw+=x(1)∗dz(1)
d w + = x ( 2 ) ∗ d z ( 2 ) dw + = x^{(2)}\ *dz^{(2)} dw+=x(2) ∗dz(2)
………….
d w + = x ( m ) ∗ d z ( m ) dw + = x^{(m)}*{dz}^{(m)} dw+=x(m)∗dz(m)
d w = d w m dw = \frac{{dw}}{m} dw=mdw
d b = 0 db = 0 db=0
d b + = d z ( 1 ) db + = {dz}^{(1)} db+=dz(1)
d b + = d z ( 2 ) db + = {dz}^{(2)} db+=dz(2)
………….
d b + = d z ( m ) db + = dz^{(m)} db+=dz(m)
d b = d b m db = \frac{{db}}{m} db=mdb
上述(伪)代码就是我们在之前实现中做的,我们已经去掉了一个for循环,但用上述方法计算 d w dw dw 仍然需要一个循环遍历训练集,我们现在要做的就是将其向量化!(也就是之前我们有两个for循环,第一个for循环是遍历m个样品的,上节课我们已经用向量化解决了,而第二个for循环时遍历m个特征值的,这次我们就要解决这个)
首先我们来看 d b db db,不难发现 d b = 1 m ∑ i = 1 m d z ( i ) db=\frac{1}{m}\sum_{i=1}^{m}dz^{(i)} db=m1i=1∑mdz(i) 之前的讲解中,我们知道所有的 d z ( i ) dz^{(i)} dz(i)已经组成一个行向量 d Z dZ dZ了,所以在Python中,我们很容易地想到 d b = 1 m n p . s u m ( d Z ) db=\frac{1}{m}np.sum(dZ) db=m1np.sum(dZ)接下来看 d w dw dw,我们先写出它的公式 d w = 1 m X d z T dw=\frac{1}{m}Xdz^{T} dw=m1XdzT 其中, X X X 是一个行向量。因此展开后 d w = 1 m ( x ( 1 ) d z ( 1 ) + x ( 2 ) d z ( 2 ) + . . . + x m d z m ) dw=\frac{1}{m}(x^{(1)}dz^{(1)}+x^{(2)}dz^{(2)}+...+x^{m}dz^{m}) dw=m1(x(1)dz(1)+x(2)dz(2)+...+xmdzm) 因此我们可以仅用两行代码进行计算: d b = 1 m n p . s u m ( d Z ) db=\frac{1}{m}np.sum(dZ) db=m1np.sum(dZ) d w = 1 m X d z T dw=\frac{1}{m}Xdz^{T} dw=m1XdzT这样,我们就避免了在训练集上使用for循环。
现在,让我们回顾一下,看看我们之前怎么实现的逻辑回归,可以发现,没有向量化是非常低效的,如下图所示代码:

我们的目标是不使用for循环,而是向量,我们可以这么做:
Z = w T X + b = n p . d o t ( w . T , X ) + b Z = w^{T}X + b = np.dot( w.T,X)+b Z=wTX+b=np.dot(w.T,X)+b
A = σ ( Z ) A = \sigma( Z ) A=σ(Z)
d Z = A − Y dZ = A - Y dZ=A−Y
d w = 1 m X d z T {{dw} = \frac{1}{m}Xdz^{T}\ } dw=m1XdzT
d b = 1 m ∗ n p . s u m ( d Z ) db= \frac{1}{m}*np.sum( dZ) db=m1∗np.sum(dZ)
w : = w − a ∗ d w w: = w - a*dw w:=w−a∗dw
b : = b − a ∗ d b b: = b - a*db b:=b−a∗db
现在我们利用前五个公式完成了前向和后向传播,也实现了对所有训练样本进行预测和求导,再利用后两个公式,梯度下降更新参数。我们的目的是不使用for循环,所以我们就通过一次迭代实现一次梯度下降,但如果你希望多次迭代进行梯度下降,那么仍然需要for循环,放在最外层。不过我们还是觉得一次迭代就进行一次梯度下降,避免使用任何循环比较舒服一些。
最后,我们得到了一个高度向量化的、非常高效的逻辑回归的梯度下降算法,我们将在下次视频中讨论Python中的Broadcasting技术。
2.15 Python 中的广播(Broadcasting in Python)
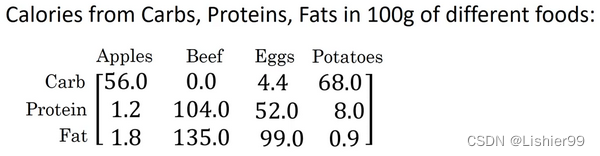
这是一个不同食物(每100g)中不同营养成分的卡路里含量表格,表格为3行4列,列表示不同的食物种类,从左至右依次为苹果,牛肉,鸡蛋,土豆。行表示不同的营养成分,从上到下依次为碳水化合物,蛋白质,脂肪。
那么,我们现在想要计算不同食物中不同营养成分中的卡路里百分比。
现在计算苹果中的碳水化合物卡路里百分比含量,首先计算苹果(100g)中三种营养成分卡路里总和56+1.2+1.8 = 59,然后用56/59 = 94.9%算出结果。
可以看出苹果中的卡路里大部分来自于碳水化合物,而牛肉则不同。
对于其他食物,计算方法类似。首先,按列求和,计算每种食物中(100g)三种营养成分总和,然后分别用不用营养成分的卡路里数量除以总和,计算百分比。
那么,能否不使用for循环完成这样的一个计算过程呢?
假设上图的表格是一个4行3列的矩阵 A A A,记为 A 3 × 4 A_{3\times 4} A3×4,接下来我们要使用Python的numpy库完成这样的计算。我们打算使用两行代码完成,第一行代码对每一列进行求和,第二行代码分别计算每种食物每种营养成分的百分比。
在jupyter notebook中输入如下代码,按shift+Enter运行,输出如下。

下面使用如下代码计算每列的和,可以看到输出是每种食物(100g)的卡路里总和。

其中
sum的参数axis=0表示求和运算按列执行,之后会详细解释。接下来计算百分比,这条指令将 3 × 4 3\times 4 3×4的矩阵 A A A除以一个 1 × 4 1 \times 4 1×4的矩阵,得到了一个 3 × 4 3 \times 4 3×4的结果矩阵,这个结果矩阵就是我们要求的百分比含量。
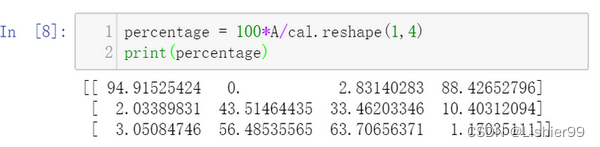
下面再来解释一下
A.sum(axis = 0)中的参数axis。axis用来指明将要进行的运算是沿着哪个轴执行,在numpy中,0轴是垂直的,也就是列,而1轴是水平的,也就是行。而第二个
A/cal.reshape(1,4)指令则调用了numpy中的广播机制。这里使用 3 × 4 3 \times 4 3×4的矩阵 A A A除以 1 × 4 1 \times 4 1×4的矩阵 c a l cal cal。技术上来讲,其实并不需要再将矩阵 c a l cal cal reshape(重塑)成 1 × 4 1 \times 4 1×4,因为矩阵 c a l cal cal本身已经是 1 × 4 1 \times 4 1×4了(cal就是卡路里总量矩阵,上面已经计算了)。但是当我们写代码时不确定矩阵维度的时候,通常会对矩阵进行重塑来确保得到我们想要的列向量或行向量。重塑操作reshape是一个常量时间的操作,时间复杂度是 O ( 1 ) O(1) O(1),它的调用代价极低。那么一个 3 × 4 3 \times 4 3×4 的矩阵是怎么和 1 × 4 1 \times 4 1×4的矩阵做除法的呢?让我们来看一些更多的广播的例子。

在numpy中,当一个 4 × 1 4 \times 1 4×1的列向量与一个常数做加法时,实际上会将常数扩展为一个 4 × 1 4 \times 1 4×1的列向量,然后两者做逐元素加法。结果就是右边的这个向量。这种广播机制对于行向量和列向量均可以使用。
再看下一个例子。
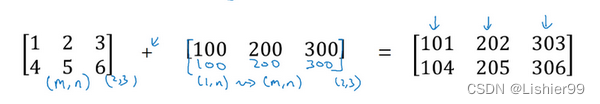
用一个 2 × 3 2 \times 3 2×3的矩阵和一个 1 × 3 1 \times 3 1×3 的矩阵相加,其泛化形式是 m × n m \times n m×n 的矩阵和 1 × n 1 \times n 1×n的矩阵相加。在执行加法操作时,其实是将 1 × n 1 \times n 1×n 的矩阵复制成为 m × n m \times n m×n 的矩阵,然后两者做逐元素加法得到结果。针对这个具体例子,相当于在矩阵的第一列加100,第二列加200,第三列加300。这就是在前一张幻灯片中计算卡路里百分比的广播机制,只不过这里是除法操作(广播机制与执行的运算种类无关)。
下面是最后一个例子
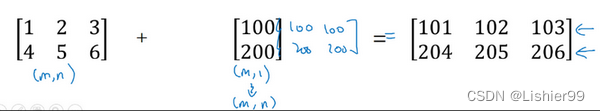
这里相当于是一个 m × n m \times n m×n 的矩阵加上一个 m × 1 m \times 1 m×1 的矩阵。在进行运算时,会先将 m × 1 m \times 1 m×1 矩阵水平复制 n n n 次,变成一个 m × n m \times n m×n 的矩阵,然后再执行逐元素加法。
广播机制的一般原则如下:

这里我先说一下我本人对numpy广播机制的理解,再解释上面这张PPT。
首先是numpy广播机制
如果两个数组的后缘维度的轴长度相符或其中一方的轴长度为1,则认为它们是广播兼容的。广播会在缺失维度和轴长度为1的维度上进行。
后缘维度的轴长度:
A.shape[-1]即矩阵维度元组中的最后一个位置的值对于图中卡路里计算的例子,矩阵 A 3 , 4 A_{3,4} A3,4 后缘维度的轴长度是4,而矩阵 c a l 1 , 4 cal_{1,4} cal1,4 的后缘维度也是4,则他们满足后缘维度轴长度相符,可以进行广播。广播会在轴长度为1的维度进行,轴长度为1的维度对应
axis=0,即垂直方向,矩阵 cal ( 1 , 4 ) \text{cal}{(1,4)} cal(1,4) 沿axis=0(垂直方向)复制成为 c a l ( t e m p ) ( 3 , 4 ) {cal_{(temp)}}{(3,4)} cal(temp)(3,4) 之后两者进行逐元素除法运算。现在解释上图中的例子
矩阵 A m , n A_{m,n} Am,n 和矩阵 B 1 , n B_{1,n} B1,n 进行四则运算,后缘维度轴长度相符,可以广播,广播沿着轴长度为1的轴进行,即 B 1 , n B_{1,n} B1,n 广播成为 B m , n ′ {B_{m,n}}' Bm,n′ ,之后做逐元素四则运算。
矩阵 A m , n A_{m,n} Am,n 和矩阵 B m , 1 B_{m,1} Bm,1 进行四则运算,后缘维度轴长度不相符,但其中一方轴长度为1,可以广播,广播沿着轴长度为1的轴进行,即 B m , 1 B_{m,1} Bm,1 广播成为 B m , n ′ {B_{m,n}}' Bm,n′ ,之后做逐元素四则运算。
矩阵 A m , 1 A_{m,1} Am,1 和常数 R R R 进行四则运算,后缘维度轴长度不相符,但其中一方轴长度为1,可以广播,广播沿着缺失维度和轴长度为1的轴进行,缺失维度就是
axis=0,轴长度为1的轴是axis=1,即 R R R广播成为 B m , 1 ′ {B_{m,1}}' Bm,1′ ,之后做逐元素四则运算。最后,对于Matlab/Octave 有类似功能的函数
bsxfun。总结一下
broadcasting,可以看看下面的图(可以理解为自适应维度):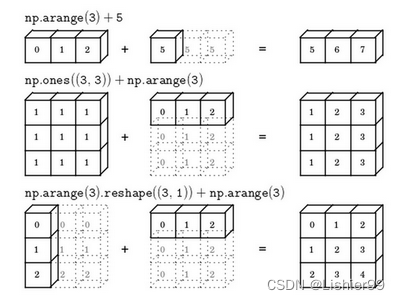
2.16 关于 python _ numpy 向量的说明(A note on python or numpy vectors)
本节主要讲Python中的numpy一维数组的特性,以及与行向量或列向量的区别。并介绍了老师在实际应用中的一些小技巧,去避免在coding中由于这些特性而导致的bug。
Python的特性允许你使用广播(broadcasting)功能,这是Python的numpy程序语言库中最灵活的地方。而我认为这是程序语言的优点,也是缺点。优点的原因在于它们创造出语言的表达性,Python语言巨大的灵活性使得你仅仅通过一行代码就能做很多事情。但是这也是缺点,由于广播巨大的灵活性,有时候你对于广播的特点以及广播的工作原理这些细节不熟悉的话,你可能会产生很细微或者看起来很奇怪的bug。例如,如果你将一个列向量添加到一个行向量中,你会以为它报出维度不匹配或类型错误之类的错误,但是实际上你会得到一个行向量和列向量的求和。
在Python的这些奇怪的影响之中,其实是有一个内在的逻辑关系的。但是如果对Python不熟悉的话,有一些学生非常生硬、非常艰难地去寻找bug。所以我在这里想做的就是分享给你们一些技巧,这些技巧对我非常有用,它们能消除或者简化我的代码中所有看起来很奇怪的bug。同时我也希望通过这些技巧,你也能更容易地写没有bug的Python和numpy代码。
为了演示Python-numpy的一个容易被忽略的效果,特别是怎样在Python-numpy中构造向量,让我来做一个快速示范。首先设置 a = n p . r a n d o m . r a n d n ( 5 ) a=np.random.randn(5) a=np.random.randn(5),这样会生成存储在数组 a a a 中的5个高斯随机数变量。之后输出 a a a,从屏幕上可以得知,此时 a a a 的shape(形状)是一个 ( 5 , ) (5,) (5,)的结构。这在Python中被称作一个一维数组。它既不是一个行向量也不是一个列向量,这也导致它有一些不是很直观的效果。举个例子,如果我输出一个转置阵,最终结果它会和 a a a看起来一样,所以 a a a和 a a a的转置阵最终结果看起来一样。而如果我输出 a a a和 a a a的转置阵的内积,即
np.dot(a,a.T),你可能会想: a a a乘以 a a a的转置返回给你的可能会是一个矩阵。但是如果我这样做,你只会得到一个数。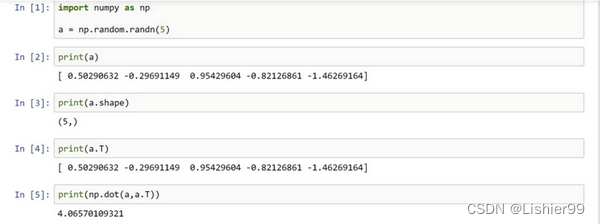
所以建议你编写神经网络时,不要使用shape为 (5,)、(n,) 或者其他一维数组的数据结构。相反,如果你设置 a a a 为 ( 5 , 1 ) (5,1) (5,1),即5行1列向量。在先前的操作里 a a a 和 a a a 的转置看起来一样,而现在这样的 a a a 变成一个新的 a a a 的转置,并且它是一个行向量。请注意一个细微的差别,在这种数据结构中,当我们输出 a a a 的转置时有两对方括号,而之前只有一对方括号,所以这就是1行5列的矩阵和一维数组的差别。
注意:两个红色箭头,前面的不是行向量,是一个一维数组(不推荐使用),后面的是行向量。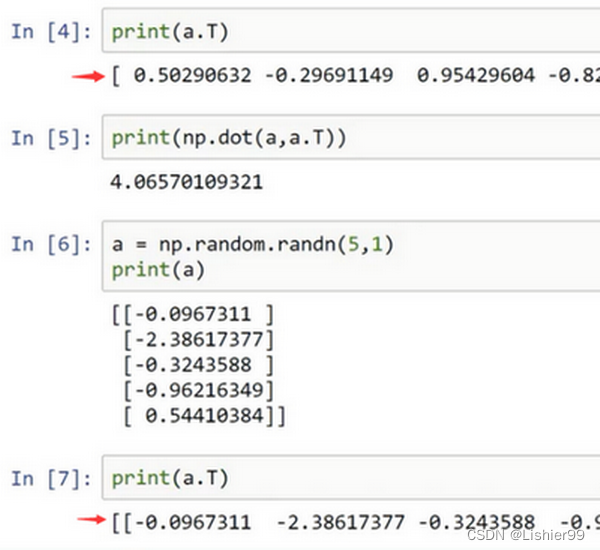
如果你输出 a a a 和 a a a 的转置的乘积,然后会返回给你一个向量的外积,所以这两个向量的外积返回给你的是一个矩阵,即行向量乘以列向量得到一个矩阵。
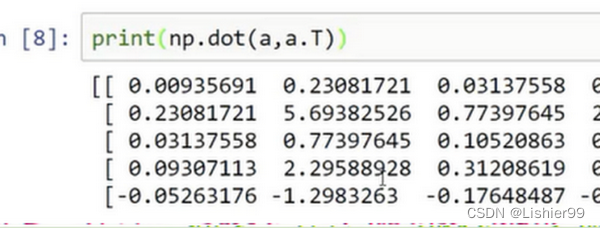
就我们刚才看到的,再进一步说明。首先我们刚刚运行的命令是这个 ( a = n p . r a n d o m . r a n d n ( 5 ) ) (a=np.random.randn(5)) (a=np.random.randn(5)),它生成了一个数据结构 a a a,其中 a . s h a p e a.shape a.shape是 ( 5 , ) (5,) (5,)。这被称作 a a a 的一维数组,同时这也是一个非常有趣的数据结构。它不像行向量和列向量那样表现的很一致,这使得它带来一些不直观的影响。所以我建议,当你在编程练习或者在执行逻辑回归和神经网络时,你不需要使用这些一维数组。

相反,如果你每次创建一个数组,你都得让它成为一个列向量,产生一个 ( 5 , 1 ) (5,1) (5,1)向量或者你让它成为一个行向量,即推荐使用向量,那么你的向量的行为可能会更容易被理解。所以在这种情况下, a . s h a p e a.shape a.shape等同于 ( 5 , 1 ) (5,1) (5,1)。这种表现很像 a a a,但是实际上却是一个列向量。同时这也是为什么当它是一个列向量的时候,你能认为这是矩阵 ( 5 , 1 ) (5,1) (5,1);同时这里 a . s h a p e a.shape a.shape 将要变成 ( 1 , 5 ) (1,5) (1,5),这就像行向量一样。所以当你需要一个向量时,我会说用这个或那个(column vector or row vector),但绝不会是一维数组。

我写代码时还有一件经常做的事,那就是如果我不完全确定一个向量的维度(dimension),我经常会扔进一个断言语句(assertion statement)。像这样,去确保在这种情况下是一个 ( 5 , 1 ) (5,1) (5,1)向量,或者说是一个列向量。这些断言语句实际上是要去执行的,并且它们也会有助于为你的代码提供信息。所以不论你要做什么,不要犹豫直接插入断言语句。如果你不小心以一维数组来执行,你也能够重新改变数组维数 a = r e s h a p e a=reshape a=reshape,表明一个 ( 5 , 1 ) (5,1) (5,1)数组或者一个 ( 1 , 5 ) (1,5) (1,5)数组,以致于它表现更像列向量或行向量,可以理解为强行将数组转换成向量。
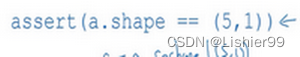
不要使用一维数组。总是使用 n × 1 n \times 1 n×1 维矩阵(基本上是列向量),或者 1 × n 1 \times n 1×n 维矩阵(基本上是行向量),这样你可以减少很多assert语句来节省核矩阵和数组的维数的时间。另外,为了确保你的矩阵或向量所需要的维数时,不要羞于 reshape 操作。
总之,我希望这些建议能帮助你解决一个Python中的bug,从而使你更容易地完成练习。
2.17 Jupyter/iPython Notebooks快速入门(Quick tour of Jupyter/iPython Notebooks)
学到现在,你即将要开始处理你的第一个编程作业。但在那之前,让我快速地给你介绍一下在Coursera上的iPython Notebooks工具。
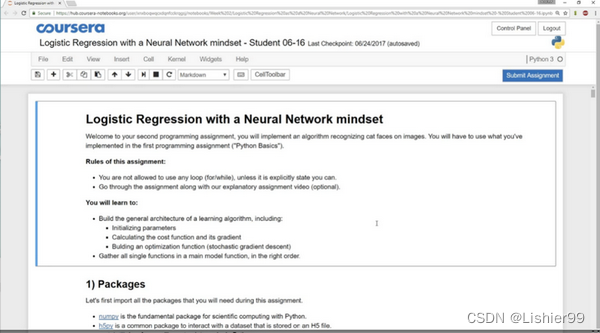
这就是Jupyter iPython Notebooks的界面,你可以通过它连接到Coursera。让我快速地讲解下它的一些特性。关于它的说明已经被写入这个Notebook中。
这里有一些空白区域的代码块,你可以在这里编写代码。有时,你也会看到一些函数块。而关于这些的说明都已经在iPython Notebook的文本中。在iPython Notebook中,在这些较长的灰色的区域就是代码块。
有时,你会看到代码块中有像这样的开始代码和结束代码。在进行编程练习时,请确保你的代码写在开始代码和结束代码之间。
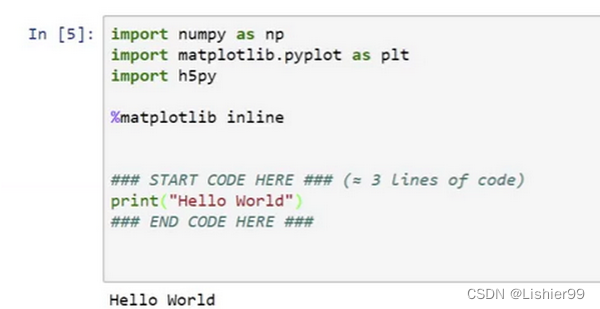
比如,编写打印输出Hello World的代码,然后执行这一代码块(你可以按shift +enter来执行这一代码块)。最终,它就会输出我们想要的Hello World。
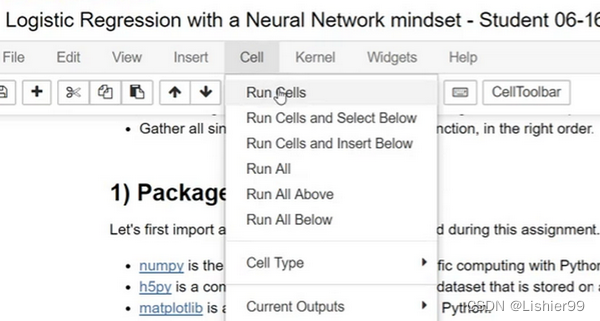
在运行一个单元格cell时,你也可以选择运行其中的一块代码区域。通过点击Cell菜单的Run Cells执行这部分代码。
也许,在你的计算机上,运行cell的键盘快捷方式可能并非是shift enter。但是,Mac应该和我的个人电脑一样,可以使用shift + enter来运行cell。
当你正在阅读指南时,如果不小心双击了它,点中的区域就会变成markdown语言形式。如果你不小心使其变成了这样的文本框,只要运行下单元格cell,就可以回到原来的形式。所以,点击cell菜单的Run Cells或者使用shift + enter,就可以使得它变回原样。
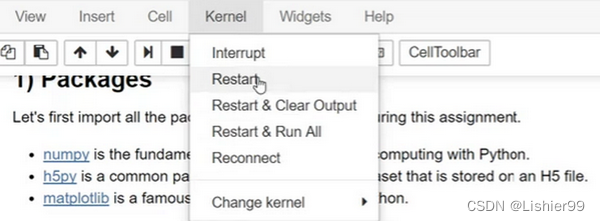
这里还有一些其他的小技巧。比如当你执行上面所使用的代码时,它实际上会使用一个内核在服务器上运行这段代码。如果你正在运行超负荷的进程,或者电脑运行了很长一段时间,或者在运行中出了错,又或者网络连接失败,这里依然有机会让Kernel重新工作。你只要点击Kernel,选择Restart,它会重新运行Kernel使程序继续工作。
所以,如果你只是运行相对较小的工作并且才刚刚启动你的ipad或笔记本电脑,这种情况应该是不会发生的。但是,如果你看见错误信息,比如Kernel已经中断或者其他信息,你可以试着重启Kernel。
当我使用iPython Notebook时会有多个代码区域块。尽管我并没有在前面的代码块中添加自己的代码,但还是要确保先执行这块代码。因为在这个例子,它导入了numpy包并另命名为np等,并声明了一些你可能需要的变量。为了能顺利地执行下面的代码,就必须确保先执行上面的代码,即使不要求你去写其他的代码。
最后,当你完成作业后,可以通过点击右上方蓝色的Submit Assignment按钮提交你的作业。
我发现这种交互式的shell命令,在iPython Notebooks是非常有用的,能使你快速地实现代码并且查看输出结果,便于学习。所以我希望这些练习和Jupyter iPython Notebooks会帮助你更快地学习和实践,并且帮助你了解如何去实现这些学习算法。后面一个视频是一个选学视频,它主要是讲解逻辑回归中的代价函数。你可以选择是否观看。不管怎样,都祝愿你能通过这两次编程作业。我会在新一周的课程里等待着你。
2.18 (选修)logistic 损失函数的解释(Explanation of logistic regression cost function)
在前面的视频中,我们已经分析了逻辑回归的损失函数表达式,在这节选修视频中,我将给出一个简洁的证明来说明逻辑回归的损失函数为什么是这种形式。
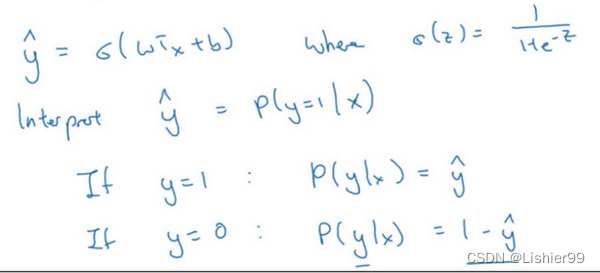
回想一下,在逻辑回归中,需要预测的结果 y ^ \hat{y} y^,可以表示为 y ^ = σ ( w T x + b ) \hat{y}=\sigma(w^{T}x+b) y^=σ(wTx+b), σ \sigma σ是我们熟悉的 S S S型函数 σ ( z ) = σ ( w T x + b ) = 1 1 + e − z \sigma(z)=\sigma(w^{T}x+b)=\frac{1}{1+e^{-z}} σ(z)=σ(wTx+b)=1+e−z1 。我们约定 y ^ = p ( y = 1 ∣ x ) \hat{y}=p(y=1|x) y^=p(y=1∣x) ,即算法的输出 y ^ \hat{y} y^ 是给定训练样本 x x x 条件下 y y y 等于1的概率。换句话说,如果 y = 1 y=1 y=1,在给定训练样本 x x x 条件下 y = y ^ y=\hat{y} y=y^;反过来说,如果 y = 0 y=0 y=0,在给定训练样本 x x x条件下 y y y 等于1减去 y ^ ( y = 1 − y ^ ) \hat{y}(y=1-\hat{y}) y^(y=1−y^),因此,如果 y ^ \hat{y} y^ 代表 y = 1 y=1 y=1 的概率,那么 1 − y ^ 1-\hat{y} 1−y^就是 y = 0 y=0 y=0的概率。接下来,我们就来分析这两个条件概率公式。
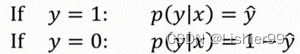
这两个条件概率公式定义形式为 p ( y ∣ x ) p(y|x) p(y∣x)并且代表了 y = 0 y=0 y=0 或者 y = 1 y=1 y=1 这两种情况,我们可以将这两个公式合并成一个公式。需要指出的是我们讨论的是二分类问题的损失函数,因此, y y y的取值只能是0或者1。上述的两个条件概率公式可以合并成如下公式:
p ( y ∣ x ) = y ^ y ( 1 − y ^ ) ( 1 − y ) p(y|x)={\hat{y}}^{y}{(1-\hat{y})}^{(1-y)} p(y∣x)=y^y(1−y^)(1−y)
接下来我会解释为什么可以合并成这种形式的表达式: ( 1 − y ^ ) (1-\hat{y}) (1−y^)的 ( 1 − y ) (1-y) (1−y)次方这行表达式包含了上面的两个条件概率公式,我来解释一下为什么。
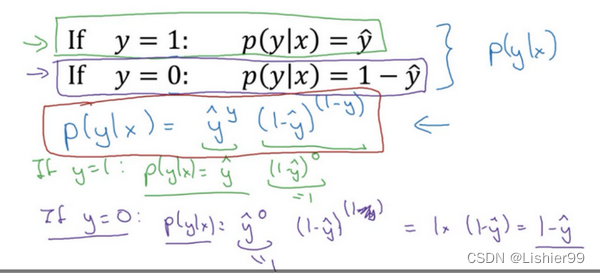
第一种情况,假设 y = 1 y=1 y=1,由于 y = 1 y=1 y=1,那么 ( y ^ ) y = y ^ {(\hat{y})}^{y}=\hat{y} (y^)y=y^,因为 y ^ \hat{y} y^的1次方等于 y ^ \hat{y} y^, 1 − ( 1 − y ^ ) ( 1 − y ) 1-{(1-\hat{y})}^{(1-y)} 1−(1−y^)(1−y)的指数项 ( 1 − y ) (1-y) (1−y)等于0,由于任何数的0次方都是1, y ^ \hat{y} y^乘以1等于 y ^ \hat{y} y^。因此当 y = 1 y=1 y=1时 p ( y ∣ x ) = y ^ p(y|x)=\hat{y} p(y∣x)=y^(图中绿色部分)。
第二种情况,当 y = 0 y=0 y=0 时 p ( y ∣ x ) p(y|x) p(y∣x) 等于多少呢? 假设 y = 0 y=0 y=0, y ^ \hat{y} y^的 y y y次方就是 y ^ \hat{y} y^ 的0次方,任何数的0次方都等于1,因此 p ( y ∣ x ) = 1 × ( 1 − y ^ ) 1 − y p(y|x)=1×{(1-\hat{y})}^{1-y} p(y∣x)=1×(1−y^)1−y ,前面假设 y = 0 y=0 y=0 因此 ( 1 − y ) (1-y) (1−y)就等于1,因此 p ( y ∣ x ) = 1 × ( 1 − y ^ ) p(y|x)=1×(1-\hat{y}) p(y∣x)=1×(1−y^)。因此在这里当 y = 0 y=0 y=0时, p ( y ∣ x ) = 1 − y ^ p(y|x)=1-\hat{y} p(y∣x)=1−y^。这就是这个公式(第二个公式,图中紫色字体部分)的结果。
因此,刚才的推导表明 p ( y ∣ x ) = y ^ ( y ) ( 1 − y ^ ) ( 1 − y ) p(y|x)={\hat{y}}^{(y)}{(1-\hat{y})}^{(1-y)} p(y∣x)=y^(y)(1−y^)(1−y),就是 p ( y ∣ x ) p(y|x) p(y∣x) 的完整定义。由于 log 函数是严格单调递增的函数,最大化 l o g ( p ( y ∣ x ) ) log(p(y|x)) log(p(y∣x)) 等价于最大化 p ( y ∣ x ) p(y|x) p(y∣x) 并且地计算 p ( y ∣ x ) p(y|x) p(y∣x) 的 log对数,就是计算 l o g ( y ^ ( y ) ( 1 − y ^ ) ( 1 − y ) ) log({\hat{y}}^{(y)}{(1-\hat{y})}^{(1-y)}) log(y^(y)(1−y^)(1−y)) (其实就是将 p ( y ∣ x ) p(y|x) p(y∣x) 代入),通过对数函数化简为:
y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ylog\hat{y}+(1-y)log(1-\hat{y}) ylogy^+(1−y)log(1−y^)
而这就是我们前面提到的损失函数的负数 ( − L ( y ^ , y ) ) (-L(\hat{y},y)) (−L(y^,y)) ,前面有一个负号的原因是当你训练学习算法时需要算法输出值的概率是最大的(以最大的概率预测这个值),然而在逻辑回归中我们需要最小化损失函数,因此最小化损失函数与最大化条件概率的对数 l o g ( p ( y ∣ x ) ) log(p(y|x)) log(p(y∣x)) 关联起来了,因此这就是单个训练样本的损失函数表达式。
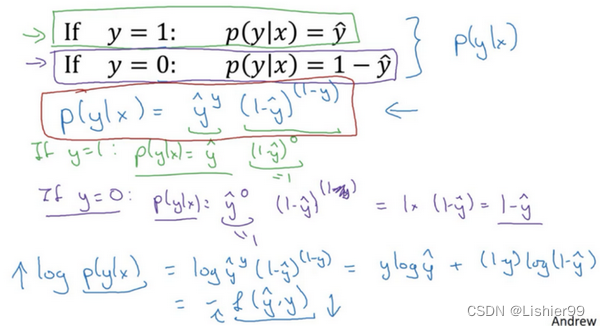
在 m m m个训练样本的整个训练集中又该如何表示呢,让我们一起来探讨一下。
让我们一起来探讨一下,整个训练集中标签的概率,更正式地来写一下。假设所有的训练样本服从同一分布且相互独立,也即独立同分布的,所有这些样本的联合概率就是每个样本概率的乘积:
P ( labels in training set ) = ∏ i = 1 m P ( y ( i ) ∣ x ( i ) ) P\left(\text{labels in training set} \right) = \prod_{i =1}^{m}{P(y^{(i)}|x^{(i)})} P(labels in training set)=∏i=1mP(y(i)∣x(i))。
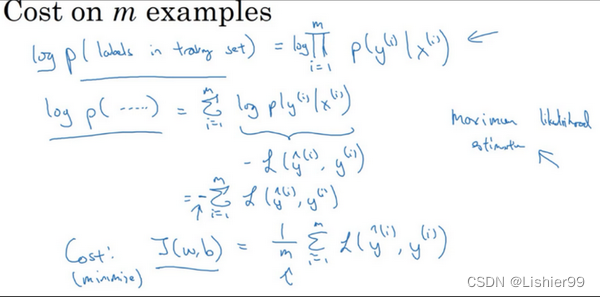
如果你想做最大似然估计,需要寻找一组参数,使得给定样本的观测值概率最大,但令这个概率最大化等价于令其对数最大化,在等式两边取对数:
l o g p ( labels in training set ) = l o g ∏ i = 1 m P ( y ( i ) ∣ x ( i ) ) = ∑ i = 1 m l o g P ( y ( i ) ∣ x ( i ) ) = ∑ i = 1 m − L ( y ^ ( i ) , y ( i ) ) logp\left( \text{labels in training set} \right) = log\prod_{i =1}^{m}{P(y^{(i)}|x^{(i)})} = \sum_{i = 1}^{m}{logP(y^{(i)}|x^{(i)})} = \sum_{i =1}^{m}{- L(\hat y^{(i)},y^{(i)})} logp(labels in training set)=log∏i=1mP(y(i)∣x(i))=∑i=1mlogP(y(i)∣x(i))=∑i=1m−L(y^(i),y(i))
在统计学里面,有一个方法叫做最大似然估计,即求出一组参数,使这个式子取最大值,也就是说,使得这个式子取最大值, ∑ i = 1 m − L ( y ^ ( i ) , y ( i ) ) \sum_{i= 1}^{m}{- L(\hat y^{(i)},y^{(i)})} ∑i=1m−L(y^(i),y(i)),可以将负号移到求和符号的外面, − ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) - \sum_{i =1}^{m}{L(\hat y^{(i)},y^{(i)})} −∑i=1mL(y^(i),y(i)),这样我们就推导出了前面给出的logistic回归的成本函数 J ( w , b ) = ∑ i = 1 m L ( y ^ ( i ) , y ( ^ i ) ) J(w,b)= \sum_{i = 1}^{m}{L(\hat y^{(i)},y^{\hat( i)})} J(w,b)=∑i=1mL(y^(i),y(^i))。
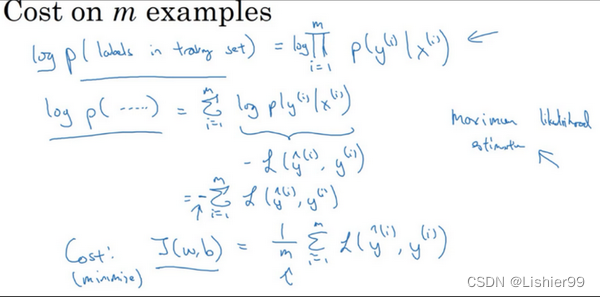
由于训练模型时,目标是让成本函数最小化,所以我们不是直接用最大似然概率,要去掉这里的负号,最后为了方便,可以对成本函数进行适当的缩放,我们就在前面加一个额外的常数因子 1 m \frac{1}{m} m1,即: J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) J(w,b)= \frac{1}{m}\sum_{i = 1}^{m}{L(\hat y^{(i)},y^{(i)})} J(w,b)=m1∑i=1mL(y^(i),y(i))。
总结一下,为了最小化成本函数 J ( w , b ) J(w,b) J(w,b),我们从logistic回归模型的最大似然估计的角度出发,假设训练集中的样本都是独立同分布的条件下。尽管这节课是选修性质的,但还是感谢观看本节视频。我希望通过本节课您能更好地明白逻辑回归的损失函数,为什么是那种形式,明白了损失函数的原理,希望您能继续完成课后的练习,前面课程的练习以及本周的测验,在课后的小测验和编程练习中,祝您好运。
-
相关阅读:
STM32 -- 做一块自己的开发板(STM32F103C8T6)
基于Springboot+Mybatis+mysql+vue宠物领养网站1.0
公司新来的阿里P7大咖,只用十分钟就教会了我实现高层次的复用
mybatis基本构成&mybatis与hibernate的区别&添加mybatis支持
jmeter的简单使用
如何学习渗透测试?怎样才能入行?
计算机毕设之基于数据可视化的智慧社区内网平台python+django+mysql(含开题+源码+部署教程)
计算机的进制转换
HTML期末学生大作业-使用HTML+CSS技术仿传智博客网站
微信小程序如何使用地球半径计算两组经纬度点之间的距离(自身位置与接口返回位置)【上】
- 原文地址:https://blog.csdn.net/weixin_43895667/article/details/126163816
