educoder_python：7-1-矩阵（numpy）

第1关：ndarray对象

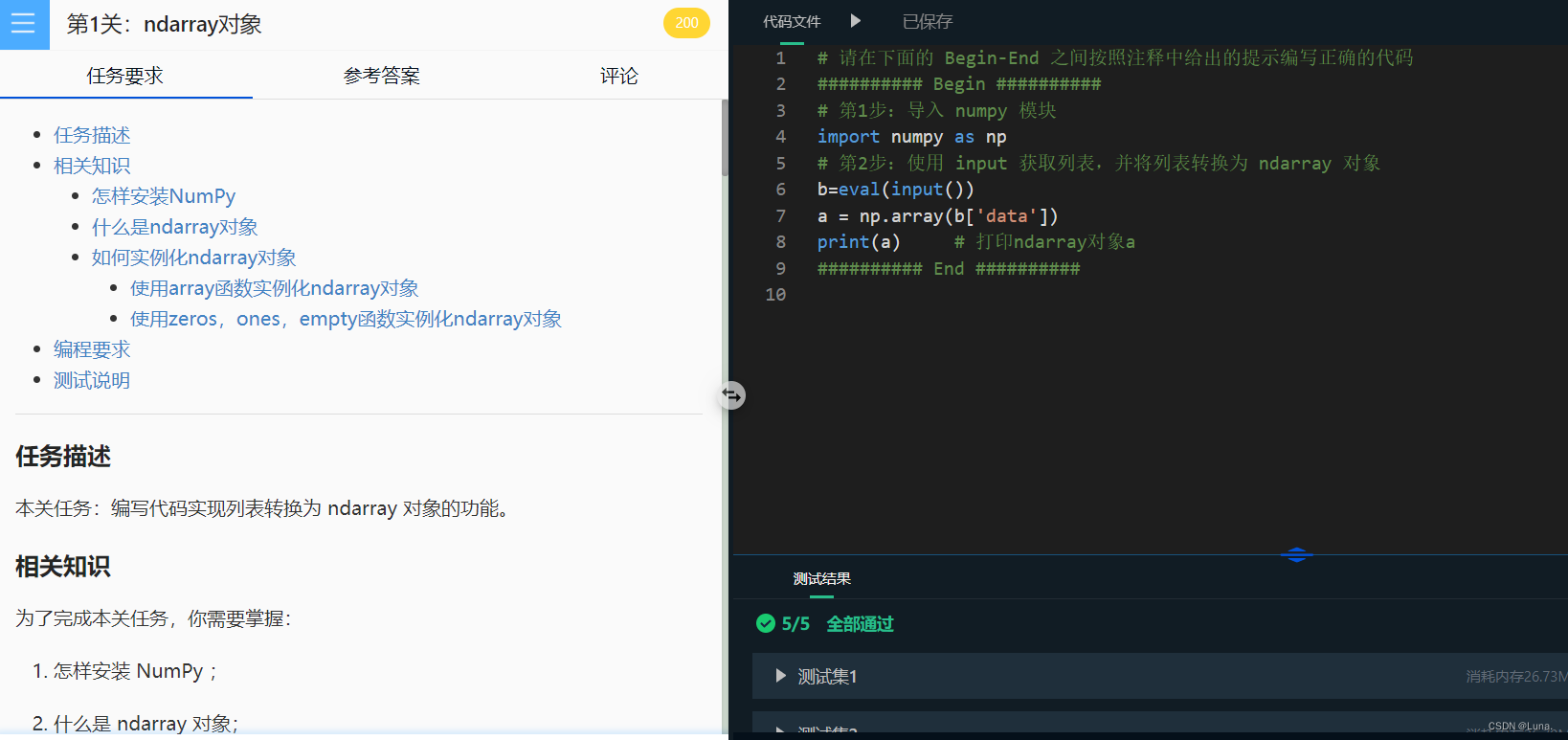
本关任务：编写代码实现列表转换为 ndarray 对象的功能。

第2关：形状操作

本关任务：使用本关所学知识完成 ndarray 对象的变形。

第3关：矩阵运算

任务描述
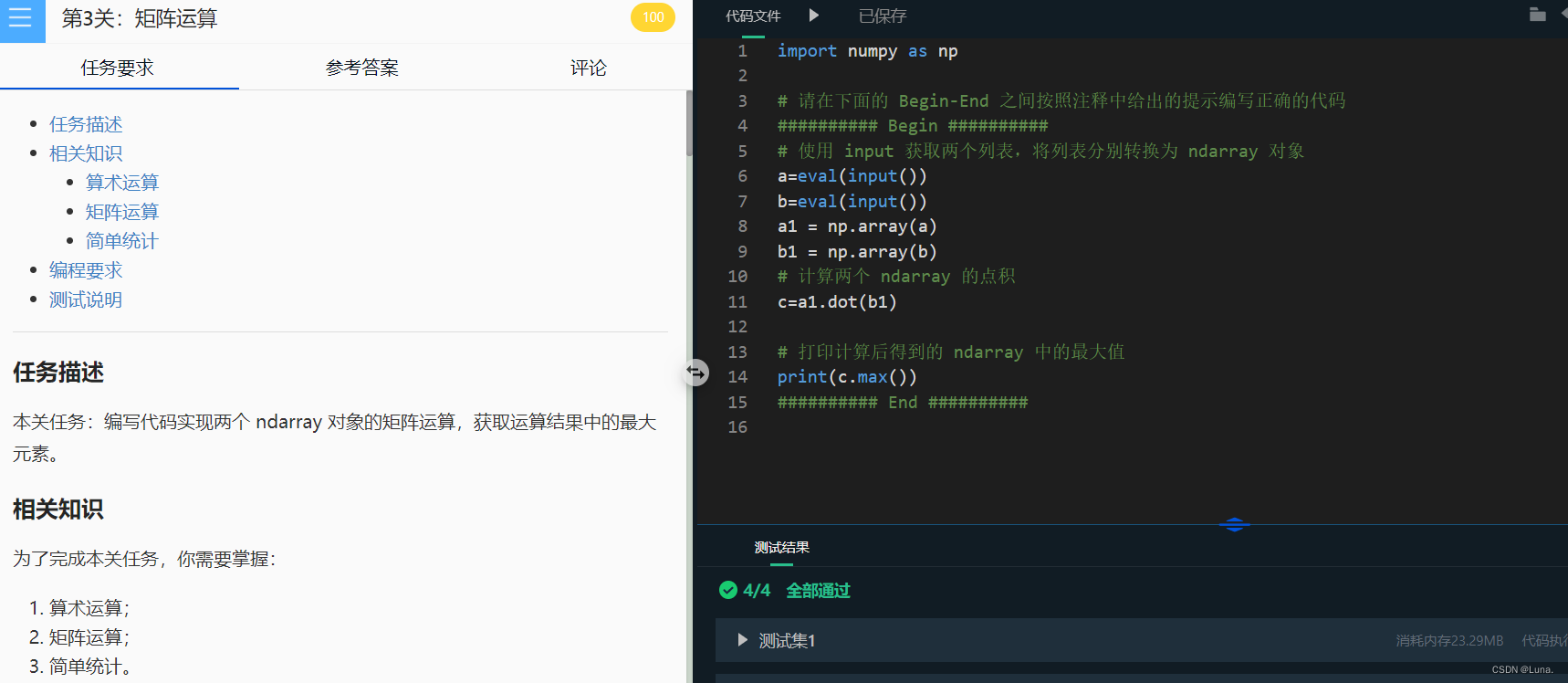
本关任务：编写代码实现两个 ndarray 对象的矩阵运算，获取运算结果中的最大元素。

相关知识
为了完成本关任务，你需要掌握：

算术运算；
矩阵运算；
简单统计。
算术运算
如果想要对 ndarray 对象中的元素做 elementwise ( 逐个元素地 )的算术运算非常简单，加减乘除即可。

第4关：随机数生成

第5关：索引与切片

第6关：数组堆叠

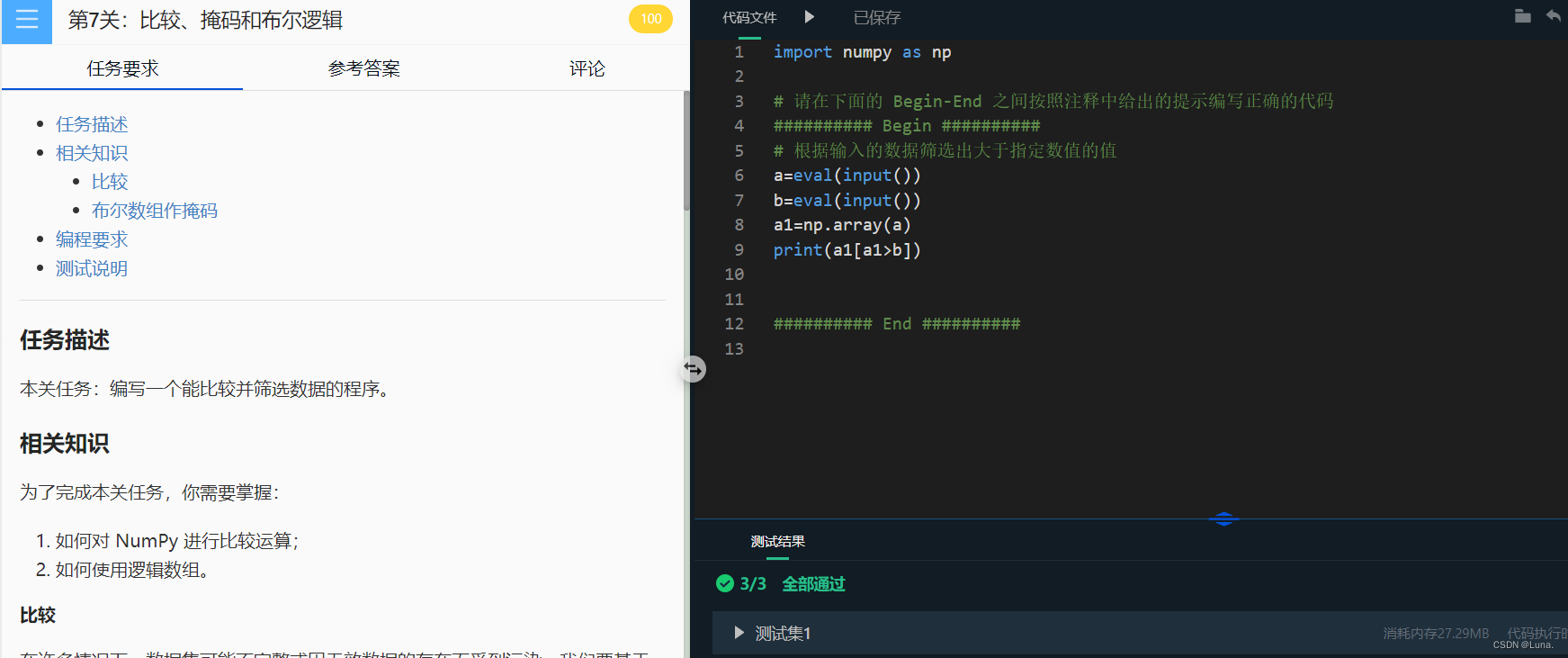
第7关：比较、掩码和布尔逻辑

第8关：索引方式

任务描述
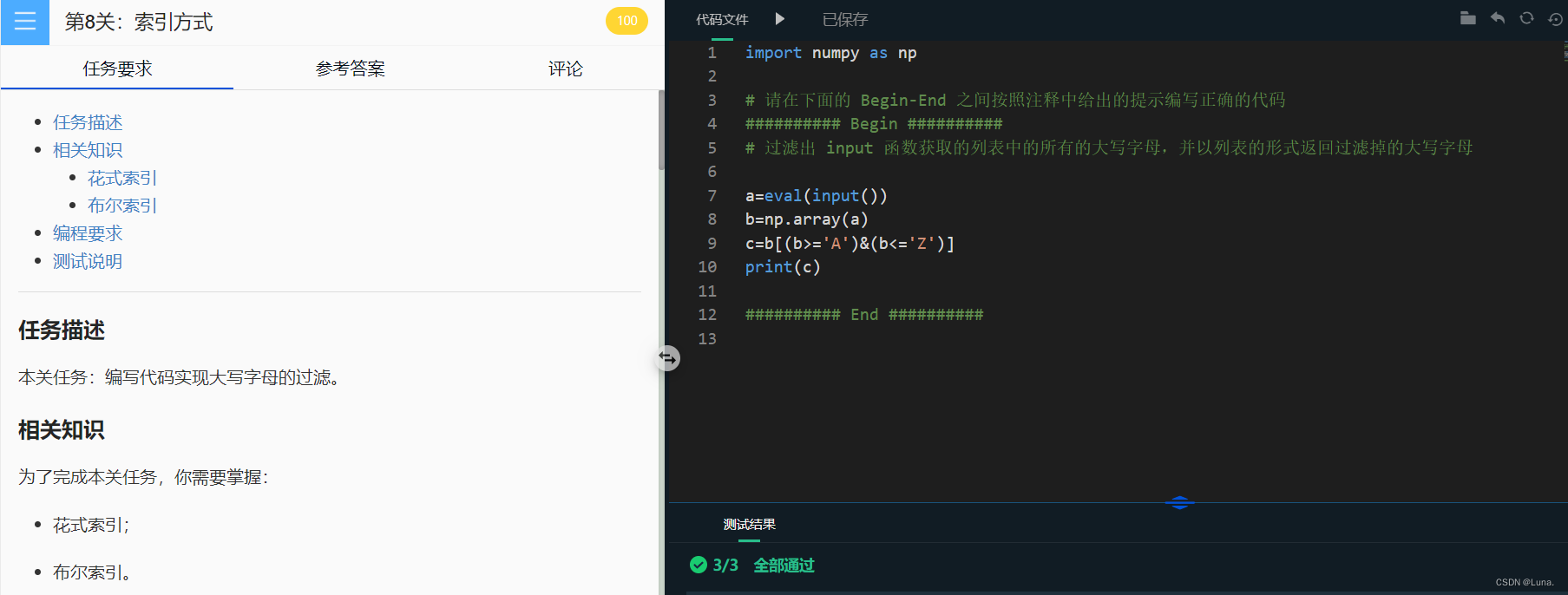
本关任务：编写代码实现大写字母的过滤。

相关知识
为了完成本关任务，你需要掌握：

花式索引；

布尔索引。

花式索引
花式索引是 NumPy 用来描述使用整型数组（这里的数组，可以是 NumPy 的数组，也可以是 Python 自带的 list）作为索引的术语，其意义是根据索引数组的值作为目标数组的某个轴的下标来取值。

使用一维整型数组作为索引，如果被索引数组是一维数组，那么索引的结果就是对应位置的元素；如果被索引数组是二维数组，那么就是对应下标的行。如图 1 所示。

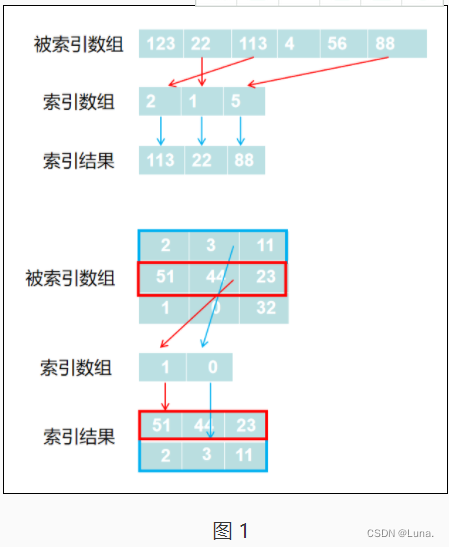
示例代码如下：

import numpy as np
arr = np.array([‘zero’,‘one’,‘two’,‘three’,‘four’])
‘’’
打印arr中索引为1和4的元素
结果为：[‘one’, ‘four’]
‘’’
print(arr[[1,4]])
arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
‘’’
打印arr中索引为1和0的行
结果为：[[4, 5, 6],
[1, 2, 3]]
‘’’
print(arr[[1, 0]])
‘’’
打印arr中第2行第1列与第3行第2列的元素
结果为：[4, 8]
‘’’
print(arr[[1, 2], [0, 1]])
布尔索引
我们可以通过一个布尔数组来索引目标数组，以此找出与布尔数组中值为True的对应的目标数组中的数据，从而达到筛选出想要的数据的功能。如下图所示：（需要注意的是，布尔数组的长度必须与被索引数组对应的轴的长度一致）

不过单纯的传入布尔数组进去有点蠢，有没有更加优雅的方式使用布尔索引来达到筛选数据的效果呢？

当然有！我们可以想办法根据我们的需求，构造出布尔数组，然后再通过布尔索引来实现筛选数据的功能。

假设有公司员工绩效指数的数据如图 2（用一个一维的 ndarray 表示），现在想要把绩效指数大于 3.5 的筛选出来进行股权激励。

有了布尔数组就可以使用布尔索引来实现筛选数据的功能了，如图 4 所示。

图 4
示例代码如下：

import numpy as np
performance = np.array([3.25, 3.5, 3.75, 3.5, 3.25, 3.75])
‘’’
筛选出绩效高于3.5的数据
结果为:[3.75, 3.75]
‘’’
print(performance[performance > 3.5])
‘’’
筛选出绩效高于3.25并且低于4的数据
注意：&表示并且的意思，可以看成是and。&左右两边必须加上()
结果为:[3.5 3.75 3.5 3.75]
‘’’
print(performance[(performance > 3.25) & (performance < 4)])
编程要求
请在右侧编辑器 Begin-End 处补充代码，过滤出 input 函数获取的列表中的所有的大写字母。

测试说明
平台会对你编写的代码进行测试，对比你输出的数值与实际正确的数值，只有所有数据全部计算正确才能进入下一关。

测试输入：

[“d”,“a”,“A”,“p”,“b”,“I”,“C”,“K”]
预期输出：

[‘A’ ‘I’ ‘C’ ‘K’]

第9关：NumPy广播机制

任务描述
本关任务：利用广播机制实现 Z-score 标准化。

相关知识
为了完成本关任务，你需要掌握：

什么是广播；
广播的原则。
什么是广播
两个 ndarray 对象的相加、相减以及相乘都是对应元素之间的操作。

import numpy as np
x = np.array([[2,2,3],[1,2,3]])
y = np.array([[1,1,3],[2,2,4]])
print(x*y)
执行结果：

[[ 2 2 9]
[ 2 4 12]]
当两个 ndarray 对象的形状并不相同的时候，我们可以通过扩展数组的方法来实现相加、相减、相乘等操作，这种机制叫做广播（broadcasting）。

比如，一个二维的 ndarray 对象减去列平均值，来对数组的每一列进行取均值化处理：

import numpy as np
arr = np.random.randn(4,3) # arr为4行3列的ndarray对象
print(arr)
print(“–”*10)
arr_mean = arr.mean(axis=0) # arr_mean为有3个元素的一维ndarray对象
print(arr_mean)
print(“–”*10)
demeaned = arr - arr_mean # 对arr的每一列进行
print(demeaned)
执行结果：

[[-0.63142643 -2.34389969 0.2514214 ]
[ 1.01460854 1.30149344 -0.4379635 ]
[ 1.97510072 2.28925691 0.92899164]
[ 1.00600092 0.14652798 -0.39323066]]

[0.84107094 0.34834466 0.08730472]

[[-1.47249737 -2.69224435 0.16411668]
[ 0.1735376 0.95314878 -0.52526822]
[ 1.13402978 1.94091225 0.84168692]
[ 0.16492998 -0.20181668 -0.48053538]]
很明显上面代码中的 arr 和 arr_mean 维度并不形同，但是它们可以进行相减操作，这就是通过广播机制来实现的。

广播的原则
广播的原则：如果两个数组的后缘维度（trailing dimension，即从末尾开始算起的维度）的轴长度相符，或其中的一方的长度为 1 ，则认为它们是广播兼容的。广播会在缺失或长度为 1 的维度上进行，这句话是理解广播的核心。

广播主要发生在两种情况，一种是两个数组的维数不相等，但是它们的后缘维度的轴长相符，另外一种是有一方的长度为 1。
我们来看一个例子：

import numpy as np
arr1 = np.array([[0, 0, 0],[1, 1, 1],[2, 2, 2], [3, 3, 3]])
arr2 = np.array([1, 2, 3])
arr_sum = arr1 + arr2
print(arr_sum)
执行结果：

[[1 2 3]
[2 3 4]
[3 4 5]
[4 5 6]]
arr1 的 shape 为 (4,3)，arr2 的 shape 为 (3,)；可以说前者是二维的，而后者是一维的，但是它们的后缘维度相等，arr1 的第二维长度为 3，和 arr2 的维度相同。如图 1 所示。

arr1 和 arr2 的 shape 并不一样，但是它们可以执行相加操作，这就是通过广播完成的，在这个例子当中是将 arr2 沿着 0 轴进行扩展。

我们再看一个例子：

import numpy as np
arr1 = np.array([[0, 0, 0],[1, 1, 1],[2, 2, 2], [3, 3, 3]]) #arr1.shape = (4,3)
arr2 = np.array([[1],[2],[3],[4]]) #arr2.shape = (4, 1)
arr_sum = arr1 + arr2
print(arr_sum)
执行结果：

[[1 1 1]
[3 3 3]
[5 5 5]
[7 7 7]]
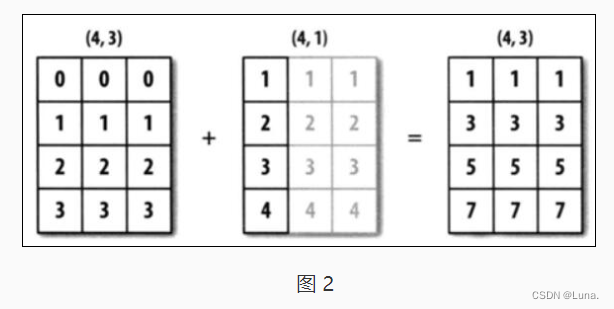
arr1 的 shape 为 (4,3)，arr2 的 shape 为 (4,1)，它们都是二维的，但是第二个数组在 1 轴上的长度为 1，所以，可以在 1 轴上面进行广播。如图 2 所示。

编程要求
请在右侧编辑器 Begin-End 处补充代码，将三个输入数据转换为 ndarray 对象并计算它们的和。

测试说明
平台会对你编写的代码进行测试，对比你输出的数值与实际正确的数值，只有所有数据全部计算正确才能进入下一关。

测试输入：

[[9, 3, 1], [7, 0, 6], [4, 6, 3]]
[1, 5, 9]
[[9], [6], [7]]
预期输出：

[[19 17 19]
[14 11 21]
[12 18 19]]