🎉🎉🎉写在前面：
博主主页：🌹🌹🌹戳一戳，欢迎大佬指点！
博主秋秋：QQ：1477649017 欢迎志同道合的朋友一起加油喔💪
目标梦想：进大厂，立志成为一个牛掰的Java程序猿，虽然现在还是一个小菜鸟嘿嘿
-----------------------------谢谢你这么帅气美丽还给我点赞！比个心-----------------------------

---

---

一，有关二叉树性质的证明

---

二，实题解析

---

---

三，二叉树相关oj题

🌟检查两棵树是否相同

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p != null &&  q == null || p == null && q != null){
            //一个为空，一个不为空的情况
            return false;
        }
        
        if(p == null && q == null){
            //两个都为空的情况
            return true;
        }
        
        if(p.val != q.val){//能走到这就说明两个都不为空
            return false;
        }
        return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);//继续去判断左子树，然后判断右子树
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

---

判断一下这题的时间复杂度为：O(min(m,n))，其中m是左边的树的节点个数，n是右边的树的节点个数，因为我们这里的最坏情况肯定是要把小的那棵树遍历完，而不是看大的树，小的树遍历完了不相同那就直接不用比较了。

---

🌟另一棵树的子树

class Solution {
    //这个函数用来判断两个树是不是相同的树
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p != null &&  q == null || p == null && q != null){
            //一个为空，一个不为空的情况
            return false;
        }
        
        if(p == null && q == null){
            //两个都为空的情况
            return true;
        }
        
        if(p.val != q.val){//能走到这就说明两个都不为空
            return false;
        }
        return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
    } 
    //子树的关系就是小于等于的关系
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(root == null){//判断一下是否存在空的情况,，递归的过程中root可能为空
            return false;
        }
        //1,可能root,subRoot本身直接就是一样的
        if(isSameTree(root,subRoot)){//如果说root是空，这里就为false，就跳不出去，导致root.left空指针异常
            return true;
        }
        //然后判断subRoot是不是root的左子树的子树或者是右子树的子树
        return isSubtree(root.left,subRoot) || isSubtree(root.right,subRoot);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

---

---

时间复杂度分析，假设root树有m个节点，subRoot树有n个节点，因为是每次递归进去判断是不是子树，那对于每次是不是子树的判断，就是看两个树是不是相同，这个过程也是一个递归。所以最坏的情况就是subRoot和root的每一个节点都判断一下是不是子树，假设root树是n个节点，subRoot树是m个节点，那最坏就是要判断n*m次，所以时间复杂度就是O(n x m)。

---

🌟二叉树的最大深度

class Solution {
    public int maxDepth(TreeNode root) {
        //最大深度就是高度
        if(root == null){
            return 0;
        }
        return Math.max(maxDepth(root.left),maxDepth(root.right)) + 1;
    }
}
1
2
3
4
5
6
7
8
9

---

时间复杂度：O(n)

---

🌟判断一棵二叉树是不是平衡二叉树

class Solution {
    public int maxDepth(TreeNode root) {
        //最大深度就是高度
        if(root == null){
            return 0;
        }
        return Math.max(maxDepth(root.left),maxDepth(root.right)) + 1;
    }

    public boolean isBalanced(TreeNode root) {
        if(root == null){
            return true;
        }
        int leftHeight = maxDepth(root.left);
        int rightHeight = maxDepth(root.right);
        if(Math.abs(leftHeight - rightHeight) > 1){
            return false;
        }else{
            return isBalanced(root.left) && isBalanced(root.right);
        }

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

---

---

时间复杂度：O(n^2)，这里也是一个嵌套的递归，isBalanced()是递归到二叉树的每一个节点，然后判断该节点是否平衡，又是要递归求左右子树的高度，所以又相当于遍历了一遍二叉树。中间存在很多的重复计算，你在计算3这个节点的左树高度时，遍历了左树，在判断9这个节点的时候，又会重复遍历到很多的节点。所以，这个方法的时间复杂度比较高，面试要求的话肯定是达不到的。

---

【解法优化：】

class Solution {
    public int maxDepth(TreeNode root) {
        //最大深度就是高度
        if(root == null){
            return 0;
        }
        int leftHeight = maxDepth(root.left);
        int rightHeight = maxDepth(root.right);
        if(leftHeight >= 0 && rightHeight >= 0 && Math.abs(leftHeight - rightHeight) <=1){
            return (Math.max(leftHeight,rightHeight)) + 1;
        }else{
            return -1;
        }
    }

    public boolean isBalanced(TreeNode root) {
        if(root == null){
            return true;
        }
        return maxDepth(root) > 0;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

---

优化之后就只走了一个递归函数。因为其实对于根节点而言，你判断它是否平衡的时候，就已经把所有的节点都要遍历完，这个过程中就可能会出现不平衡的情况，这个时候这棵树已经就是不平衡的了，没必要再递归判断左子树右子树的节点了。现在的时间复杂度就降到了O(n)。

---

🌟判断一棵二叉树是否对称

class Solution {
    public boolean isSymmetricChild(TreeNode leftTree,TreeNode rightTree){
        //左右两边的节点的情况
        if(leftTree != null && rightTree == null || leftTree == null && rightTree != null){
            return false;//对称位置上的节点一个是空，一个不是空
        }
        if(leftTree == null && rightTree == null){
            return true;
        }
        if(leftTree.val != rightTree.val ){
            return false;//这里不能是相等return true,，因为是整棵树是否对称，还得继续往下判断
        }
        //走到这就是两个都不是空并且值相等，然后再继续往下判断
        return isSymmetricChild(leftTree.left,rightTree.right) && isSymmetricChild(leftTree.right,rightTree.left);

    }

    public boolean isSymmetric(TreeNode root) {
        if(root == null){
            return true;
        }
        return isSymmetricChild(root.left,root.right);//判断左子树，右子树是不是对称
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

---

---

🌟二叉树的分层遍历

【前导：】

void levelOrder(TreeNode root){
    if(root == null){
        return;//二叉树为空，那就直接return掉
    }
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);//首先就把root入队
    while(!queue.isEmpty()){
        TreeNode cur = queue.poll();//队头元素出队
        System.out.print(cur.val + " ");//打印元素的值
        if(cur.leftChild != null){
            queue.offer(cur.leftChild);//如果cur的左孩子不为空就入队
        }
        if(cur.rightChild != null){
            queue.offer(cur.rightChild);//如果cur的右孩子不为空就入队
        }

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

---

层序遍历的过程得用到队列，因为队列是先进先出，符合我们层序遇到节点就打印的特点。首先把根节点入队，然后只要队列不为空就出队队头元素，出对的同时会把这个元素的左孩子，右孩子入队，就这样一直循环下去，最终的打印结果就是层序的结果。

---

那么下面的分层遍历，只不过是要我们把每一层都区分开。那我们只要在每次出队之前看一下队列中的元素个数，那就是这一层的个数，并且保证每次出的时候都把这一层出完，然后每层元素都会被加入到ArrayList中，这样就被区分开了。

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> ret = new ArrayList<>();//用来存储整个结果
        if(root == null){
            return ret;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);//首先就把root入队
        while(!queue.isEmpty()){
            int size = queue.size();//先看一下队列中的元素
            List<Integer> list = new ArrayList<>();//用来存储每一行的结果
            while(size != 0){//把每一行元素出完
                TreeNode cur = queue.poll();//队头元素出队
                size--;
                if(cur.left != null){
                    queue.offer(cur.left);//如果cur的左孩子不为空就入队
                }
                if(cur.right != null){
                    queue.offer(cur.right);//如果cur的右孩子不为空就入队
                }
                list.add(cur.val);//把这个出的元素加入到list中
            }
            ret.add(list);//把这一行的结果加入到ret中
        }
        return ret;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

---

---

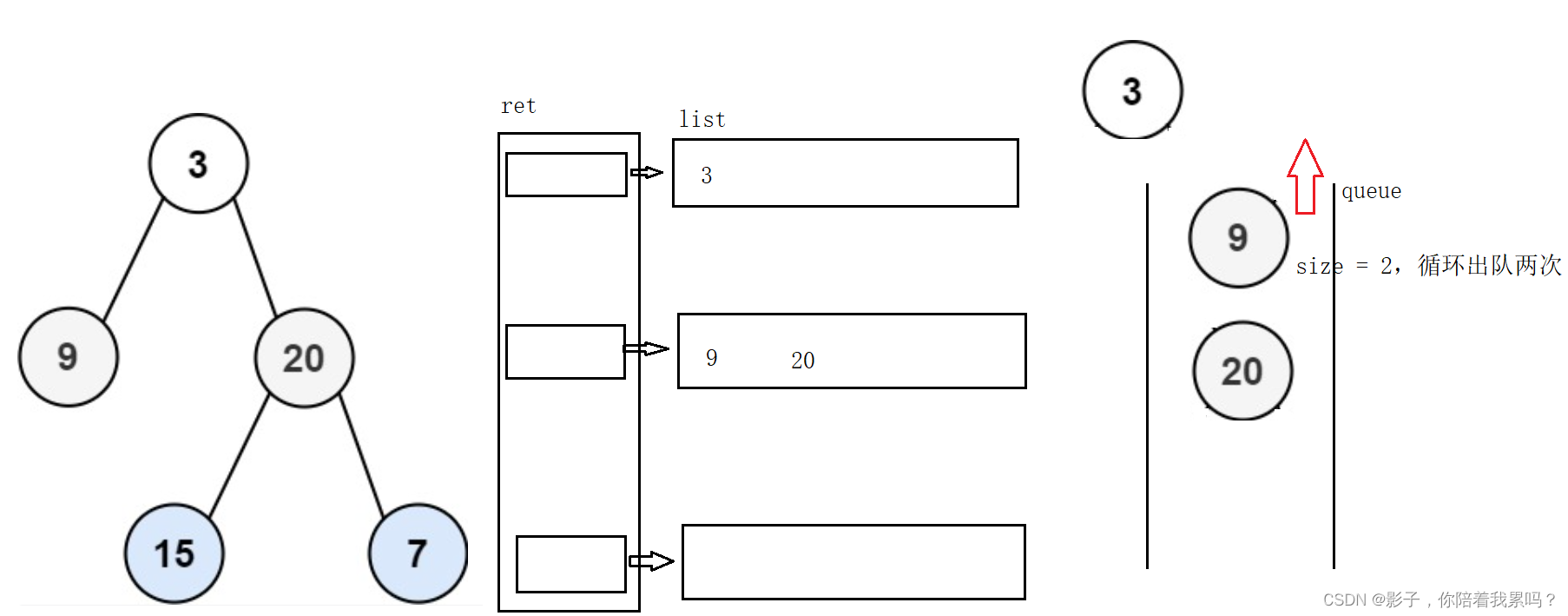
分层遍历的题记住就是用队列解，比如之前阿里考过的题，求一棵树的左视图，右视图，其实就只是上面这个题，ret这个ArrayList每一个元素的第一个元素组合起来就是左视图，最后一个元素组合起来就是右视图。

---

🌟二叉树的构建和遍历

import java.util.Scanner;
class TreeNode{
    public char val;
    public TreeNode left;
    public TreeNode right;
    public TreeNode(char val){
        this.val = val;
    }
}

public class Main{
    public static int i = 0;
    public static TreeNode creatTree(String s){//递归创建二叉树
        TreeNode root = null;
        if(s.charAt(i) != '#'){
            root = new TreeNode(s.charAt(i));
            i++;
            root.left = creatTree(s);
            root.right = creatTree(s);
        }else{
            i++;
        }
        return root;
    }
    
    public static void inOrder(TreeNode root){//中序遍历
        if(root == null){
            return ;
        }
        inOrder(root.left);
        System.out.print(root.val + " ");
        inOrder(root.right);
    }
    
    public static void main(String args[]){
        Scanner scan = new Scanner(System.in);
        while(scan.hasNextLine()){
            String s = scan.nextLine();
            TreeNode root = creatTree(s);
            inOrder(root);
        }
        
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

---

它给你的字符串是前序遍历出来的字符串顺序，所以我们就按照它的那个顺序递归创建就行。如果当前字符不是#，那就先把该节点创建，然后去递归创建其左子树，然后再是右子树。我们把每个节点串起来的过程就是你返回节点的过程。

---

🌟求二叉树指定节点的公共祖先

【解法一：】

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null){
            return null;
        }
        if(p == root || q == root){//p,q就是root，那么root就是公共祖先
            return root;
        }
        //不是，就去左右两边找
        TreeNode leftFind = lowestCommonAncestor(root.left,p,q);
        TreeNode rightFind = lowestCommonAncestor(root.right,p,q);
        if(leftFind !=null && rightFind != null){
            //就说明在两边都找到了，所以是处在root的左右两边
            return root;
        }else if(leftFind != null){
            return leftFind;
        }else{
            return rightFind;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

---

这里只是以二叉搜索树为例，其中值的比较在本题是不需要的，因为题目要求的就只是二叉树就行，但是p,q可能存在的情况就是如上。所以我们就先判断p,q是不是在root处，然后再去左边找，再去右边找，然后看两个返回值的情况。

---

【解法二：】

class Solution {
    public boolean getPath(TreeNode root,TreeNode findNode,Stack<TreeNode> stack){
        if(root == null){//如果findNode为空，那就说明找不到
            return false;//root是递归过程中可能变为空
        }
        stack.push(root);
        if(root == findNode){
            return true;//看看当前root是不是就是我们要找的
        }
        //不是，再去左边找，右边找
        boolean ret1 = getPath(root.left,findNode,stack);
        if(ret1){
            return true;//这里不能是没找到return false，因为右边可能存在
        }
        boolean ret2 = getPath(root.right,findNode,stack);
        if(ret2){
            return true;
        }
        //代码走到这了，就说明左右都没找到,那说明改root左右两边没有，那这个元素也就不是我们路径上的
        stack.pop();//把这个栈顶元素pop掉
        return false;
    }
    
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null){
            return null;
        }
        Stack<TreeNode> stackP = new Stack<>();
        Stack<TreeNode> stackQ = new Stack<>();
        boolean ret1 = getPath(root,p,stackP);
        boolean ret2 = getPath(root,q,stackQ);
        if(ret1 == true && ret2 == true){
            if(stackP.size() > stackQ.size()){
                int len = stackP.size() - stackQ.size();
                while(len != 0){
                    stackP.pop();
                    len--;
                }
            }else{
                int len = stackQ.size() - stackP.size();
                while(len != 0){
                    stackQ.pop();
                    len--;
                }
            }
        }
        while(!stackP.isEmpty() && !stackQ.isEmpty()){
            if(stackP.peek() == stackQ.peek()){
                return stackP.peek();
            }
            stackP.pop();
            stackQ.pop();
        }
        return null;//到这说明没有公共祖先
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

---

🌟二叉树转换成双向链表

import java.util.*;
public class Solution {
    public TreeNode prev = null;
    public void inOrder(TreeNode root){
        if(root == null){
            return ;
        }
        inOrder(root.left);
        root.left = prev;
        if(prev != null){//第一次的时候不需要改前驱的后继
            prev.right = root;
        }
        prev = root;
        inOrder(root.right);
    }
    public TreeNode Convert(TreeNode pRootOfTree) {
        if(pRootOfTree == null){
            return null;
        }
        inOrder(pRootOfTree);
        TreeNode head = pRootOfTree;
        while(head.left != null){
            head = head.left;
        }
        return head;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

---

🌟根据二叉树的前序中序遍历构建二叉树

class Solution {
    public int preIndex = 0;
    private TreeNode buildChildTree(int[] preorder, int[] inorder,int begin,int end){
        if(begin > end){
            return null;
        }
        TreeNode root = new TreeNode(preorder[preIndex]);//首先构建根节点
        int fIndex = findIndex(inorder,preorder[preIndex],begin,end);//在中序遍历的数组中找到这个头节点的位置
        preIndex++;//这个节点构建完了并且找完了就把preIndex++
        root.left = buildChildTree(preorder,inorder,begin,fIndex - 1);
        root.right = buildChildTree(preorder,inorder,fIndex + 1,end);
        return root;
    }

    private int findIndex(int[] inorder,int findNum,int begin,int end){
        for(int i = begin;i <= end;i++){
            if(inorder[i] == findNum){
                return i;
            }
        }
        return -1;
    }

    public TreeNode buildTree(int[] preorder, int[] inorder) {

        return buildChildTree(preorder,inorder,0,inorder.length - 1);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

---

🌟根据二叉树的中序后序遍历构建二叉树

class Solution {
    public int postIndex;//记录我们前序遍历数组的下标
    private TreeNode buildChildTree(int[] postorder, int[] inorder,int begin,int end){
        if(begin > end){
            return null;
        }
        TreeNode root = new TreeNode(postorder[postIndex]);//首先构建根节点
        int fIndex = findIndex(inorder,postorder[postIndex],begin,end);//在中序遍历的数组中找到这个头节点的位置
        postIndex--;//这个节点构建完了并且找完了就把postIndex--
        root.right = buildChildTree(postorder,inorder,fIndex + 1,end);//先构建右树，因为后序遍历根节点后是右子树的节点
        root.left = buildChildTree(postorder,inorder,begin,fIndex - 1);
        return root;
    }

    private int findIndex(int[] inorder,int findNum,int begin,int end){
        for(int i = begin;i <= end;i++){
            if(inorder[i] == findNum){
                return i;
            }
        }
        return -1;
    }

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        postIndex = postorder.length - 1;
        return buildChildTree(postorder,inorder,0,inorder.length - 1);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

原理和上面前序中序构建是一样的，只不过后序遍历的数组我们遍历的时候是从后往前，在构建子树的时候我们也是先构建右树再构建左树。

---

🌟二叉树创建字符串

class Solution {
    public String tree2str(TreeNode root) {
        if(root == null){
            return null;
        }
        StringBuilder stringBuilder = new StringBuilder();
        tree2strChild(root,stringBuilder);
        return stringBuilder.toString();
    }
    private void tree2strChild(TreeNode t,StringBuilder stringBuilder){
        if(t == null){
            return ;
        }
        stringBuilder.append(t.val);
        if(t.left != null){
            stringBuilder.append("(");
            tree2strChild(t.left,stringBuilder);
            stringBuilder.append(")");
        }else{
            if(t.right != null){
                stringBuilder.append("()");
            }else{
                return;//左右两边都为空，什么也不做
            }
        }

        if(t.right != null){
            stringBuilder.append("(");
            tree2strChild(t.right,stringBuilder);
            stringBuilder.append(")");
        }else{
            return ;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

---

🌟二叉树的前序遍历非递归实现

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        List<Integer> list = new ArrayList<>();
        TreeNode cur = root;
        while(cur != null  || !stack.empty()){
            while(cur != null){//能压入栈一定是不为空
                stack.push(cur);
                list.add(cur.val);//遇到就入栈
                cur = cur.left;
            }
            //如果cur为空了
            TreeNode top = stack.pop();
            cur = top.right;
        }
        return list;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

---

🌟二叉树的中序遍历非递归实现

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        List<Integer> list = new ArrayList<>();
        TreeNode cur = root;
        while(cur != null  || !stack.empty()){
            while(cur != null){//能压入栈一定是不为空
                stack.push(cur);
                cur = cur.left;
            }
            //如果cur为空了，也就是左边为空
            TreeNode top = stack.pop();
            list.add(top.val);//中间就可以加入到list里面了
            cur = top.right;//继续去访问右边
        }
        return list;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

---

🌟二叉树的后序遍历非递归实现

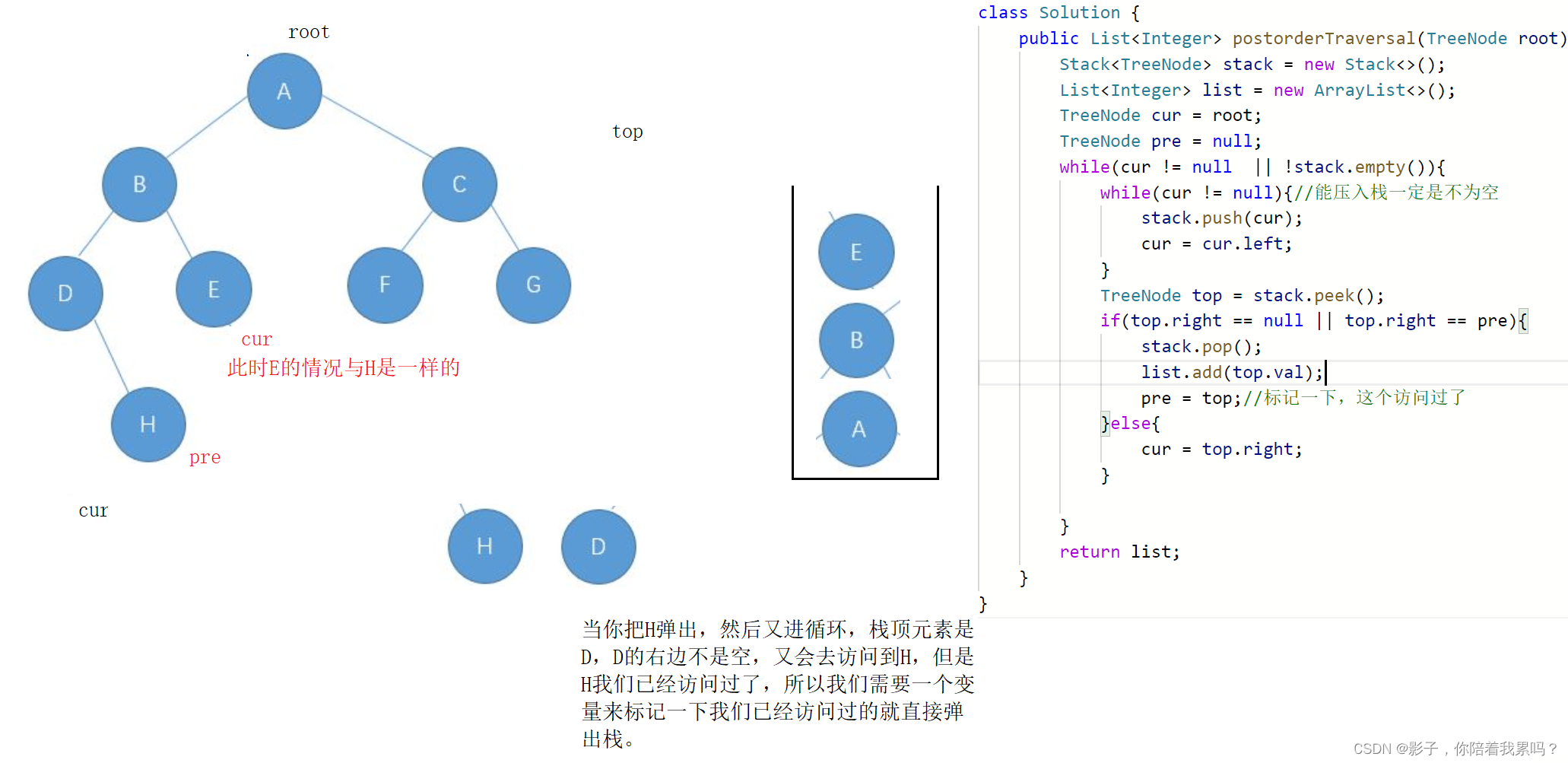
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        List<Integer> list = new ArrayList<>();
        TreeNode cur = root;
        TreeNode pre = null;
        while(cur != null  || !stack.empty()){
            while(cur != null){//能压入栈一定是不为空
                stack.push(cur);
                cur = cur.left;
            }
            TreeNode top = stack.peek();
            if(top.right == null || top.right == pre){
                stack.pop();
                list.add(top.val);
                pre = top;//标记一下，这个访问过了
            }else{
                cur = top.right;
            }
            
        }
        return list;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

---

今天关于二叉树的分享就到这了，后面会陆陆续续的恢复更新了的，大家持续关注哟，如果觉得写的不错的话还请点点赞咯，十分感谢呢！🥰🥰🥰