-
学习笔记:机器学习优化算法之牛顿法、拟牛顿法
活动地址:CSDN21天学习挑战赛
1 简介
牛顿法也叫牛顿迭代法,它是一种求根算法,也可以求函数的极小值。它的基本思想是在现有极小点估计值附近对f(x)做二阶泰勒展开,找到下一个极小点,继续迭代的过程。
2 牛顿法原理
输入:目标函数f(x),函数梯度为
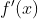 ,计算精度
,计算精度 
输出:f(x)的零点
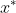
(1)选出初始值
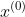 ,k=0;
,k=0;(2)计算
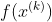 和梯度
和梯度 ;
;(3)带入迭代公式进行参数更新:
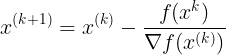
推导该迭代公式
设第k次迭代点为
 ,过该点做曲线的切线,斜率则为
,过该点做曲线的切线,斜率则为 ,进而可得到切线方程为:
,进而可得到切线方程为: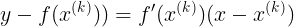
接着求该曲线与x轴的交点坐标:
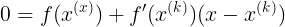
则交点的横坐标为新的迭代点的横坐标,整理得:
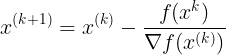
确定迭代次数或者精度;
(4)如果
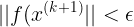 ,停止迭代,令
,停止迭代,令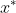 =
=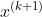 ,输出结果;否则继续迭代。
,输出结果;否则继续迭代。实验部分:雷神之锤代码计算
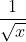
- #include
- using namespace std;
- //计算 1/((x)^(1/2))
- float Q_rsqrt( float number ) {
- long i;
- float x2, y;
- const float threeHalfs = 1.5f;
- x2 = number * 0.5f;
- y = number;
- i = * ( long * ) &y; // evil floating point bit level hacking
- i = 0x5f3759df - ( i >> 1 ); // What the fuck?
- y = * ( float * ) &i;
- y = y * ( threeHalfs - ( x2 * y * y ) ); // 1st iteration
- // y = y * ( threeHalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
- return y;
- }
- int main() {
- float x1=4;
- float x2=2;
- float x3=25;
- printf("%f",Q_rsqrt(x3));
- return 0;
- }
2.1 Hessen矩阵
Hessen矩阵存储了二阶可导的多元函数的二阶导数,Hessen矩阵可用于多元函数的泰勒展开,一般用H表示 Hessen矩阵。
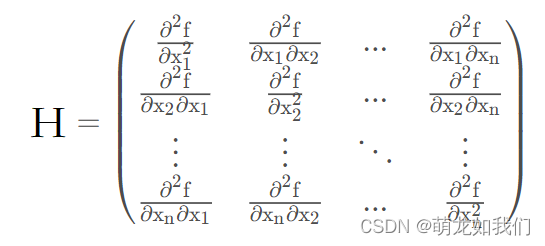
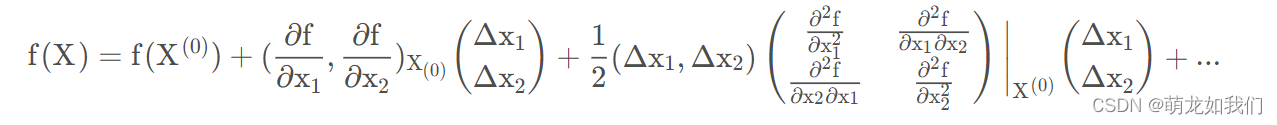
上式可简写为:
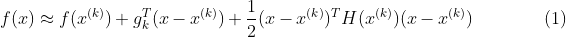
其中
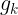 为求导后在第k个迭代点的梯度向量;
为求导后在第k个迭代点的梯度向量;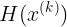 表示第k次迭代时的Hessen矩阵
表示第k次迭代时的Hessen矩阵当f(x)去到最值时,f'(x)=0,令此时的x=k+1(其中
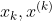 意思相同)
意思相同)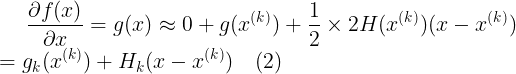
整理后得到x的迭代公式:
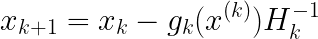
2.2 拟牛顿法条件
对(2)式子操作:
记
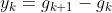 ,
,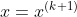 ,则:
,则: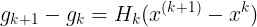

记
 代入上式得:
代入上式得: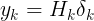
即
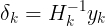 该式为拟牛顿法条件。
该式为拟牛顿法条件。从这里可以看出此时牛顿法需要 计算矩阵的逆,计算会很麻烦,甚至不存在逆矩阵,这样就需要拟牛顿法了。
3 拟牛顿法
拟牛顿法的思想是找到矩阵的逆的替代者,主要有DFP和DFGS方法。
参考
(43条消息) 泰勒展开与黑塞矩阵(Hessian Matrix)_老实人小李的博客-CSDN博客_泰勒展开式的矩阵形式
-
相关阅读:
JVM相关知识点
【ESP 保姆级教程】疯狂Node.js服务器篇 ——教室WiFi自动打卡考勤(飞书群信息+NodeJs)
实验十二 运算符重载
R3LIVE代码详解(一)
slamplay:用C++实现的SLAM工具集
海外推广运营的技巧汇总
Git学习 —— 在IDEA中使用Git
【Luogu】 P3206 [HNOI2010] 城市建设
JS进阶——构造函数&数据常用函数
无代码开发平台搭建的管理系统是什么样子?
- 原文地址:https://blog.csdn.net/qq_44635691/article/details/126148283
