⭐️前面的话⭐️

本篇文章介绍来自牛客试题广场的两道题题解，分别为【统计每个月兔子的总数】和【字符串通配符】，展示语言java。

📒博客主页：未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创，CSDN首发！
📆首发时间：🌴2022年8月3日🌴
✉️坚持和努力一定能换来诗与远方！
💭推荐书籍：📚《算法》，📚《算法导论》
💬参考在线编程网站：🌐牛客网🌐力扣
博主的码云gitee，平常博主写的程序代码都在里面。
博主的github，平常博主写的程序代码都在里面。
🍭作者水平很有限，如果发现错误，一定要及时告知作者哦！感谢感谢！

---

---

---

⭐️统计每个月兔子的总数⭐️

🔐题目详情

有一种兔子，从出生后第3个月起每个月都生一只兔子，小兔子长到第三个月后每个月又生一只兔子。

例子：假设一只兔子第3个月出生，那么它第5个月开始会每个月生一只兔子。

一月的时候有一只兔子，假如兔子都不死，问第n个月的兔子总数为多少？

数据范围：输入满足 1≤n≤31

输入描述：

输入一个int型整数表示第n个月

输出描述：

输出对应的兔子总数

示例1

输入：

3
1

输出：

2
1

题目链接：统计每个月兔子的总数

💡解题思路

基本思路： 斐波拉契数列，动态规划
解题思路：

根据题意，我们不难发现，3+个月的兔子数为两个月前兔子数。
毕竟到第三月的兔子至少得经过两个月的成长。
状态定义： 不妨设第i个月的兔子为f[i]，则上个月的兔子为f[i-1]，满三月的兔子数为f[i-2]。
状态转移方程： 不难得知f[i]=f[i-1]+f[i-2]，其中i>2
初始状态: f[1]=1,f[2]=1。

其实就是一个斐波拉契数列，由于很熟悉了，就直接采用优化版的解法吧，直接取a为f[i-2]，b为f[i-1]，f为f[i]，f[i]=a+b，每轮一次更新a，b值即可。

🔑源代码

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        
        int n = sc.nextInt();
        if (n <= 2) {
            System.out.println(n);
            return;
        }
        int a = 1;
        int b = 1;
        int f = 1;
        while (n - 2 > 0) {
            f = a + b;
            a = b;
            b = f;
            --n;
        }
        System.out.println(f);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

🌱总结

本题为斐波拉契数列构造题，递推，动态规划都可以解决，不过递归会有很多次的重复计算。

⭐️字符串通配符⭐️

🔐题目详情

问题描述：在计算机中，通配符一种特殊语法，广泛应用于文件搜索、数据库、正则表达式等领域。现要求各位实现字符串通配符的算法。
要求：
实现如下2个通配符：
*：匹配0个或以上的字符（注：能被*和?匹配的字符仅由英文字母和数字0到9组成，下同）
？：匹配1个字符

注意：匹配时不区分大小写。

输入：
通配符表达式；
一组字符串。

输出：

返回不区分大小写的匹配结果，匹配成功输出true，匹配失败输出false

数据范围：字符串长度：1≤s≤100

进阶：时间复杂度：O(n²) ，空间复杂度：O(n)

输入描述：

先输入一个带有通配符的字符串，再输入一个需要匹配的字符串

输出描述：

返回不区分大小写的匹配结果，匹配成功输出true，匹配失败输出false

示例1

输入：

te?t*.*
txt12.xls
1
2

输出：

false
1

示例2

输入：

z
zz
1
2

输出：

false
1

示例3

输入：

pq
pppq
1
2

输出：

false
1

示例4

输入：

**Z
0QZz
1
2

输出：

true
1

示例5

输入：

?*Bc*?
abcd
1
2

输出：

true
1

示例6

输入：

h*?*a
h#a
1
2

输出：

false
1

说明：

根据题目描述可知能被*和?匹配的字符仅由英文字母和数字0到9组成，所以?不能匹配#，故输出false      
1

示例7

输入：

p*p*qp**pq*p**p***ppq
pppppppqppqqppqppppqqqppqppqpqqqppqpqpppqpppqpqqqpqqp
1
2

输出：

false
1

题目链接：字符串通配符

💡解题思路

基本思路： 动态规划

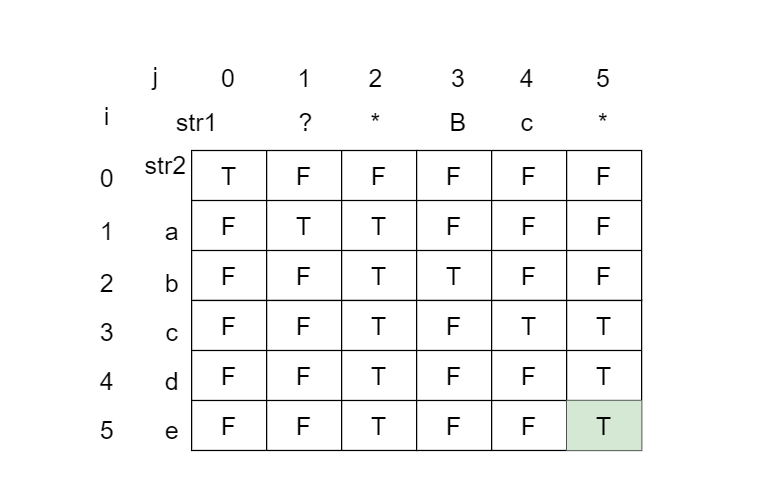
解题思路：

状态定义： 定义dp[i][j]为str1前j个字符是否与str2前i个字符是否匹配。
确定初始状态： dp[0][0]=true 如果str1[i]=='*'，dp[0][j]=dp[0][j-1]。
状态转移方程： 以下比较均为不区分大小写比较。
情况1：str1[j] 为除了*,?以外的字符或str1[j] 为*,?且str2[i]为数字字母以外的字符。
如果str1[j]==str2[i] ,取决于str1前j-1个字符是否与str2前i-1个字符是否匹配，则dp[i][j]=dp[i-1][j-1]
如果str1[j]!=str2[i] ,dp[i][j]=false

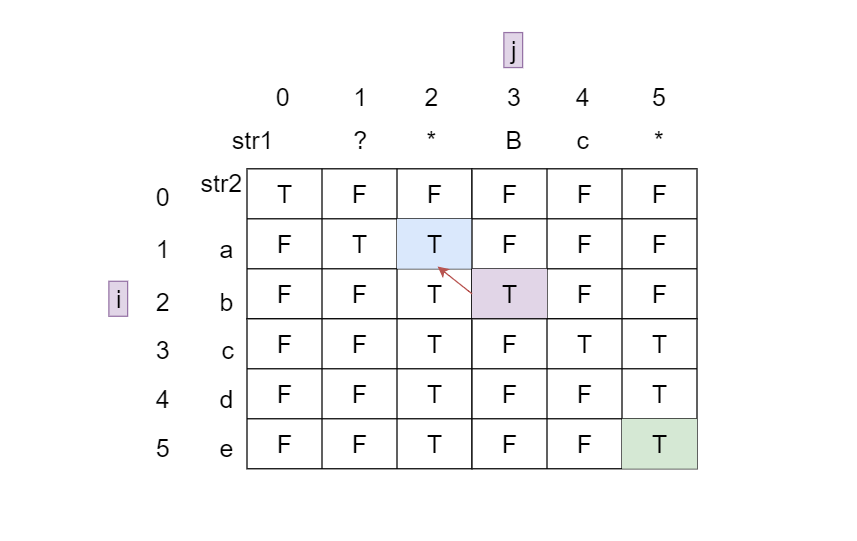
情况2：str1[j] 为*且str2[i]为数字或字母。
如果str1前j-1个字符与str2前i个字符匹配，str1加上一个*仍与str2前i个字符匹配，即dp[i][j]=dp[i][j-1]
如果str1前j个字符与str2前i-1个字符匹配，str2加上一个字母或数字字符仍与str1前i个字符匹配，即dp[i][j]=dp[i-1][j]
如果str1前j-1个字符与str2前i-1个字符匹配，str1加上一个*仍与str2加上一个字母或数字匹配，即dp[i][j]=dp[i-1][j-1]
综合，取三种情况的并集，即dp[i][j] = dp[i-1][j] || dp[i][j-1] || dp[i-1][j-1]

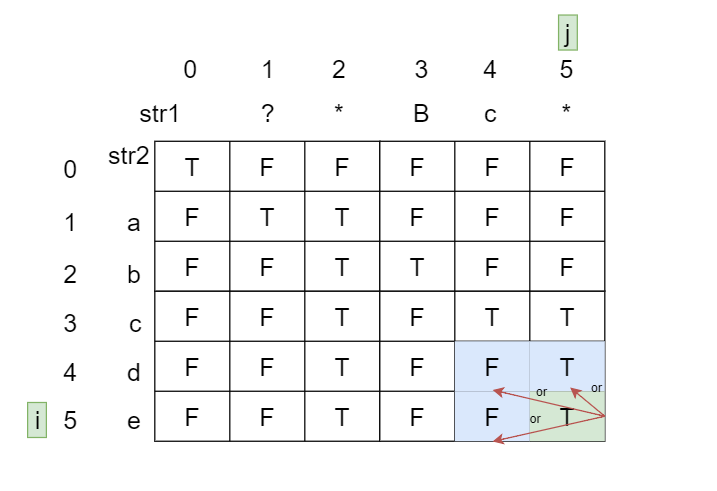
情况3：str1[j] 为?且str2[i]为数字或字母。
？能表示任意一个字母或数字，所以取决于str1前j-1个字符是否与str2前i-1个字符是否匹配，则dp[i][j]=dp[i-1][j-1]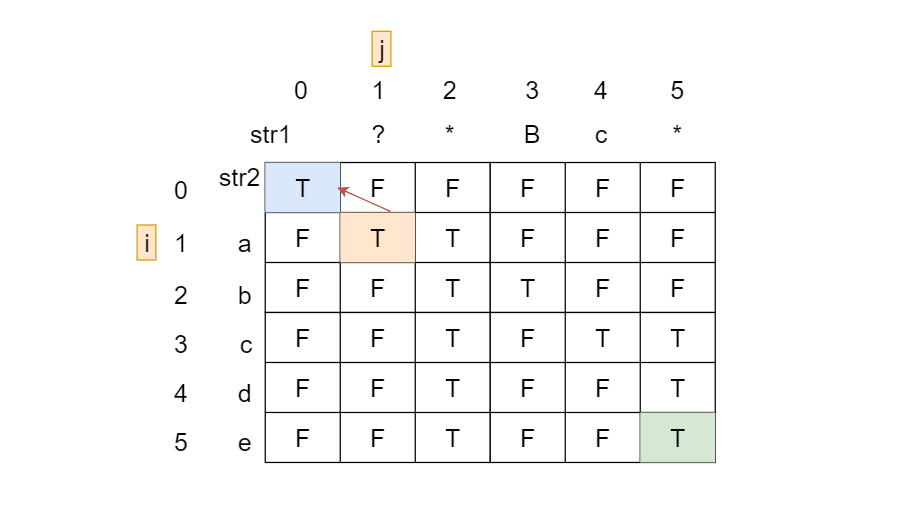

🔑源代码

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        while (sc.hasNext()) {
            String str1 = sc.nextLine();
            String str2 = sc.nextLine();
            str1 = str1.toLowerCase();
            str2 = str2.toLowerCase();
            int n = str1.length();
            int m = str2.length();
            char[] cs1 = str1.toCharArray();
            char[] cs2 = str2.toCharArray();
            boolean[][] dp = new boolean[m + 1][n + 1];
            //初始化dp[0][0] = true,如果cs1中的第一个字符为*，那dp[0][1]=true,
            //后面如果还是*,dp[0][j]=dp[0][j-1],综合dp[0][j]=dp[j-1]
            dp[0][0] = true;
            for (int j = 1; j <= n; j++) {
                if (cs1[j - 1] == '*'){
                    dp[0][j] = dp[0][j-1];
                }
            }
            for (int i = 1; i <= m; i++) {
                for (int j = 1; j <= n; j++) {
                    if (cs1[j - 1] == cs2[i - 1]) {
                        //dp[i][j] = dp[i-1][j-1]
                        dp[i][j] = dp[i - 1][j - 1];
                    } else if (cs1[j - 1] == '?' && isDigitOrAlphabet(cs2[i - 1])) {
                        //注：能被*和?匹配的字符仅由英文字母和数字0到9组成
                        dp[i][j] = dp[i - 1][j - 1];
                    } else if (cs1[j - 1] == '*' && isDigitOrAlphabet(cs2[i - 1])) {
                        //dp[i][j] = dp[i-1][j] || dp[i][j-1] || dp[i-1][j-1]
                        dp[i][j] = dp[i - 1][j] || dp[i][j - 1] || dp[i - 1][j - 1];
                    }
                    //其他情况dp[i][j]就是false，数组的值默认false，所以不用改了
                }
            } 
            System.out.println(dp[m][n]);
        }
        
    }
    private static boolean isDigitOrAlphabet(char c) {
        return c >= '0' && c <= '9' || c >= 'a' && c <= 'z';
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

🌱总结

本题为字符串匹配题，也是二维是态规划问题，难点在于问题的抽象与状态定义以及状态转移方程的推导。

类似题：
【难度:hard】44. 通配符匹配
【难度::hard】10. 正则表达式匹配

---

觉得文章写得不错的老铁们，点赞评论关注走一波！谢谢啦！