leetcode二叉树系列(二)

1、二叉树展开为链表

二叉树展开为链表

题目描述：

 1）暴力拼接

思路：就是遍历每一个节点root，找到当前节点左子树的最右节点pre，

pre.right = root.right

root.right = root.left

root.left = null

这样遍历每一个节点，就可以去掉所有节点的左子树

代码如下：

public void flatten(TreeNode root) {
    TreeNode pre;
    while (root!=null){
        //左子树为空，则跳过
        if (root.left == null) {
            root = root.right;
        } else {
            pre = root.left;
            //找到当前节点左子树的最右节点
            while (pre.right != null) pre = pre.right;
            pre.right = root.right;
            root.right = root.left;
            root.left = null;
            root = root.right;
        }
    }

2)先序遍历拼接

思路：根据先序遍历的顺序依次，把左子树拼接到右子树

代码如下：

TreeNode pre;
public void flatten(TreeNode root) {
    if(root == null) return;
    TreeNode left = root.left;
    TreeNode right = root.right;
    root.left = null;
    if(pre != null) pre.right = root;
    pre = root;
    flatten(left);
    flatten(right);
}

3)后序遍历拼接(变种)

思路：于先序遍历完全相反，由右子树最右节点开始，依次拼接

代码：

TreeNode last;
public void flatten(TreeNode root) {
    if (root == null ) return;
    flatten(root.right);
    flatten(root.left);
    //pre表示最后一个节点，依次往上建立
    root.right = last;
    root.left = null;
    last = root;
}

总结：这道题万变不离其宗，根据先序遍历的顺序，把左子树拼接到右子树，了解这点就很简单

2、二叉树中的最大路径和

二叉树中的最大路径和

题目描述：

 

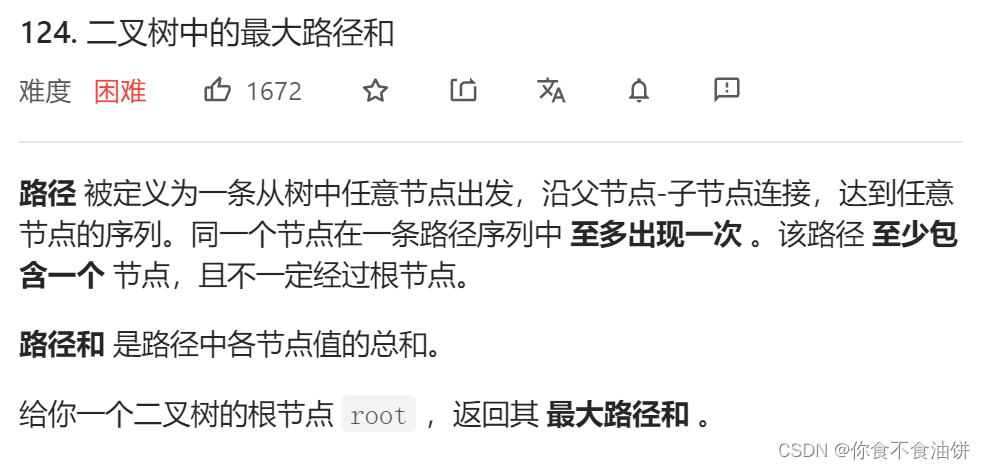
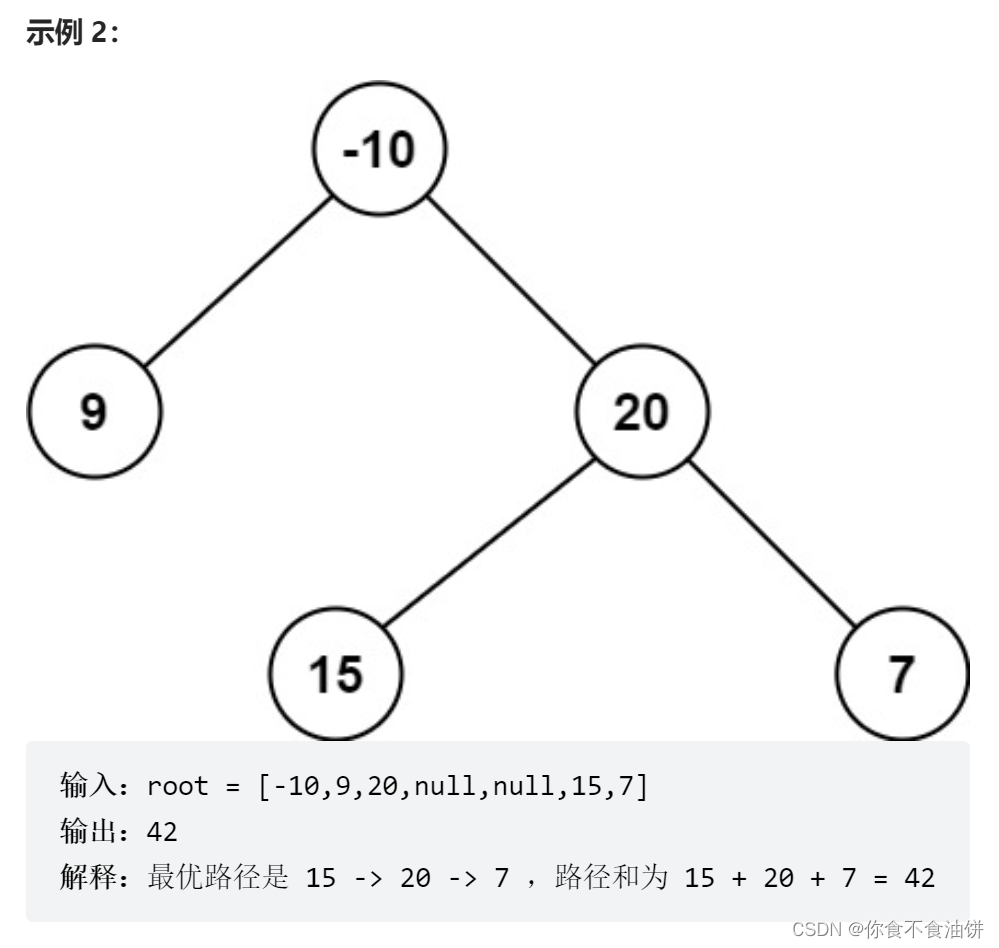
 思路：题目是要我们求最大路径和，规定路径的节点只能出现一次

 

 如图路径一般有四种情况

1. 我自己就是一条路径
2. 只跟左子节点合并成一条路径
3. 只跟右子节点合并成一条路径
4. 以自己为桥梁，跟左、右子节点合并成一条路径

我们就需要用到递归，求出每一个结点的2、3情况，并返回较大的路径和

同时，在每次递归时，都需要不断进行最大路径和的判断，因为我们不知道在哪个节点时会取到最大路径和！

进入代码：

int max = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
    dfs(root);
    return max;
}
public int dfs(TreeNode root){
  if (root == null) return 0;
  //由于路径加起来可能是负的，所以做一个比较
  int leftPath = Math.max(0,dfs(root.left));
  int rightPath = Math.max(0,dfs(root.right));
  
  max = Math.max(max,root.val + leftPath + rightPath);
  //返回左边路径和或者右边路径和的较大值
  return root.val + Math.max(leftPath,rightPath);
}

持续更新中~~