第2章-矩阵及其运算-矩阵运算(2)

from sympy.matrices import *
1.加减
A1=Matrix[1,1,1]
A2=Matrix[1,2,1]
A=A1+A2
A=A1-A2

2.数乘
a=10
A1=Matrix[1,1,1]
A=a*A1

3.矩阵乘积
注意:只有当第一个矩阵(左矩阵)的列数等于第二个矩阵(右矩阵)的行数,两个矩阵才能相乘
结果: A1(m,s)*A2(s,n)=A(m,n)
A1=Matrix(2,3,[1,1,1,1,2,2])   #A1(2,3)
A2=Matrix(3,2,[2,2,1,1,1,1])   #A2(3,2) 
A=A1*A2  #A(2,2)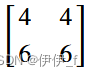



扩展: A1*A2=A1@A2=A1.dot(A2)  点积

4.矩阵的幂乘
注意:矩阵必须为方矩阵(n,n) 
结果: A**2=A*A,  A**3=A*A*A
A=Matrix(3,3,[2,2,2,2,2,2,2,2,2]) #A(3,3)
m=A**2   

5.矩阵的转置A.T
就是行列转化
A=Matrix(2,2,[1,2,3,4])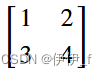

A.T

6.对称矩阵
定义:如果一个矩阵A的转置等于其本身即A=A.T, 则A称为对称矩阵
A1=eye(3)
A2=A1.T
A2


7.矩阵的行列式
注意: 矩阵必须是方阵才有行列式
A1=eye(3)
A.det()

8.矩阵代数余子式A.cofactor(i,j)
A=Matrix(3,3,[1,2,3,4,5,6,7,8,9])
A.cofactor(1,2)

9.矩阵的伴随矩阵 A.adjugate()
A=Matrix(3,3,[1,2,3,4,5,6,7,8,9])
A.adjugate()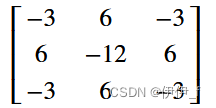

10.矩阵的秩A.rank()
A=Matrix(3,3,[1,2,3,4,5,6,7,8,9])
A.rank() 

11.逆矩阵
注意:矩阵可逆的条件：|A|!=0
from sympy.matrices import *
A=Matrix(2,2,[1,2,3,7]) 
A1=A.det()   #|A|
A2=A.adjugate()   #A的伴随矩阵
A4=1/A1*A2         #A的逆矩阵
或使用公式求
A3=A.inv()    #A的逆矩阵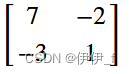

12.矩阵行列操作
12.1 寻址取值
A=Matrix(2,2,[1,2,3,4])
A[1]  #2   取第1行第2列的数
A[1,1] #4  取第2行第2列的数
A[:,1]  #    取所有行的第2列的数即取第2列数
A[0:2,1]  #取所有行的第2列的数即取第2列数
A[0,:]     #取所有列的第1行的数即取第1行数 

12.2函数取值
(1)A.row(i) 取某一行
(2)A.row([i,j,k])取多行
A=Matrix(3,3,[1,2,3,4,5,6,7,8,9])
A.row([0,2])    #等于A[[0,2],:]

(3)A.col(i)
(4)A.col([i,j,k])
(5)A.row_insert(p,M)
(6)A.col_insert(p,M)
(7)A.row_del(i)
(8)A.col_del(i)