Spearman、Pearson相关系数

首先分别简单介绍一下我们可能最常用到的Pearson和Spearman相关系数是什么东西，不写公式，尽量说得通俗易懂。Pearson相关系数很简单，是用来衡量两个数据集的线性相关程度。而Spearman相关系数不关心两个数据集是否线性相关，而是单调相关，Spearman相关系数也称为等级相关或者秩相关（即rank）。下面几个图看一看应该很容易理解：

应该很快就能理解，如果对数据进行线性变换（y = ax + b; a ≠ 0），两者相关系数的绝对值都不会发生变化（要考虑下正负）；如果对数据进行单调但不线性的变换（比如最常见的log scale），Spearman相关系数的绝对值也不会发生变化。

从以上我们就可以知道，两者的前提假设就不同，Pearson相关假设数据集在同一条直线上，而Spearman只要求单调递增或者递减，所以Pearson的统计效力比Spearman要高。但是更重要的是，你得根据你的实际情况选择正确的假设。比如，某个实验做了两次技术或者生物学重复，那有理由假设这两次重复线性相关。而如果是一个基因和另一个受到调控的基因的表达水平，或者某个基因顺式作用元件的染色质开放程度，和这个基因表达水平之间的关系就可能只需要假设单调相关。

到这里选择Pearson还是Spearman相关系数就已经解释得差不多了，但是想要更加深入了解，后面还想说一说两者的适用条件和特点。Pearson相关系数要求统计资料要是连续型变量，并且符合正态分布，而Spearman相关系数没有这个要求；Pearson相关系数在出现奇异值，或者长尾分布的时候稳定性差，不太靠，而Spearman要相对稳健很多。下面给个简单的例子：

# 在100-130的范围随机生成30个点
a <- sample(100:130, 30)
b <- sample(100:130, 30)
df <- data.frame(a, b)
# 画散点图，线性拟合
ggplot(df, aes(x=a, y=b)) + geom_smooth(method="lm") + geom_point() + xlim(0, 140) + ylim(0, 140)
# 计算Pearson和Spearman相关系数
cor.test(a, b, method="pearson")
cor.test(a, b, method="spearman")
##########################################
# 再往坐标(0, 0)追加一个点
a <- append(a, 0)
b <- append(b, 0)
df <- data.frame(a, b)
# 再次画散点图，线性拟合
ggplot(df, aes(x=a, y=b)) + geom_smooth(method="lm") + geom_point() + xlim(0, 140) + ylim(0, 140)
# 再次计算Pearson和Spearman相关系数
cor.test(a, b, method="pearson")
cor.test(a, b, method="spearman")

画图展示如下，可以看到只需要增加一个离群的点，就可以让Pearson相关系数从“不相关”变为“强相关”，而Spearman相关系数表现就要稳健得多：

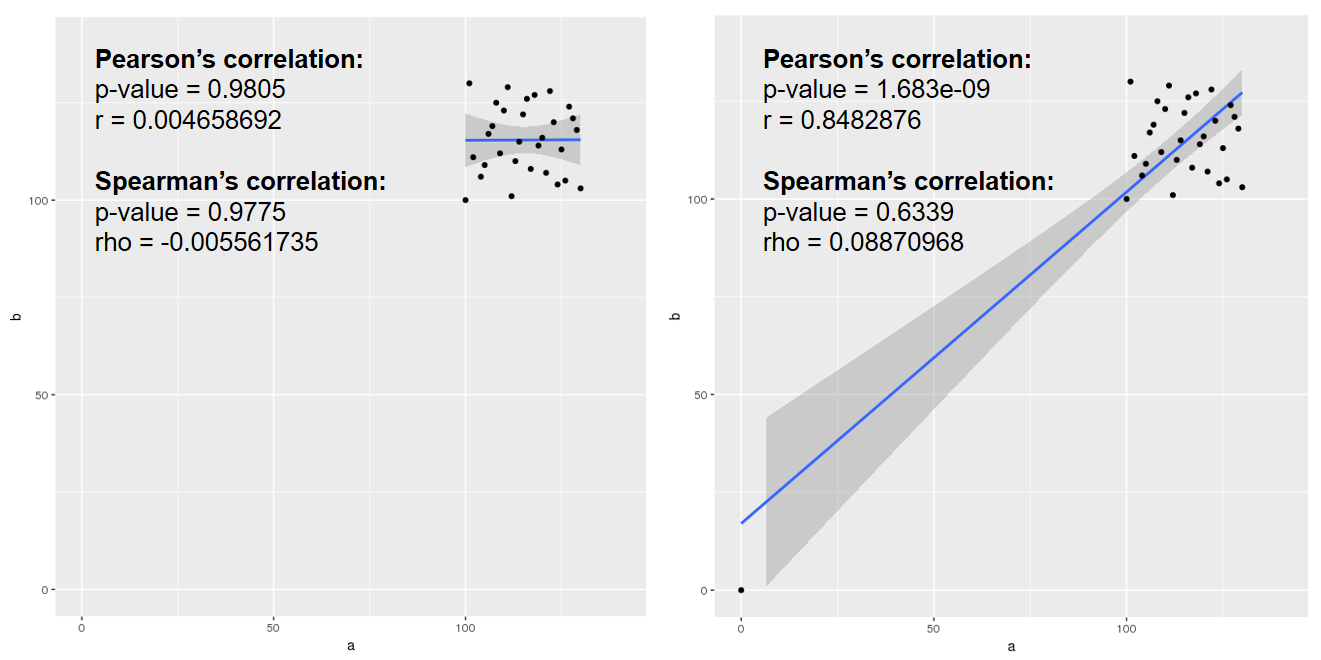
而在实际生信分析中容易出问题的地方就是转录组样品重复相关性分析。目前一般文章中或者公司给的结题报告中用得比较多的还是Pearson相关系数。但其实转录组测序的表达量不符合正态分布，并且通常都有个很长的“尾巴”（一些极高表达的基因），会导致Pearson相关系数分析的结果可靠性不佳；另外也很重要的一点，重复的假设应该不仅仅是线性相关，理想情况下应该是y = x，所以最终线性拟合得到的斜率和截距也应该有所体现。

对于第一个问题，当然你不可能因为转录组不符合正态分布就换用Spearman，因为那样统计效力更差了。Pearson作为大家最常用的方法，用一用问题也不大。如果追求更可靠的结果可以在做Pearson相关性分析之前先对数据做做变换。但除此之外请务必加上其他方法进行验证，比如聚类，不要仅仅使用Pearson相关系数。

对于第二个问题，我觉得可以在图中给出线性拟合的公式，另外也有一个专门为此类问题而生的相关性分析算法：Lin's concordance correlation coefficient，简称ccc。在谷歌学术中用关键词"concordance correlation"和RNA-seq搜一搜，也不少文章开始用这个方法了，但也通常同时搭配上Pearson相关系数：

至于搞不清小写r，大写R，以及R-square（R方）的区别和联系，似乎也是个重灾区，后面有时间有心情再写吧。

参考资料

• A comparison of the Pearson and Spearman correlation methods - Minitab Express