上一篇博客：【DR_CAN-MPC学习笔记】1.最优化控制和MPC基本概念

介绍了MPC的3个步骤：

Step1：估计/测量读取当前系统状态（可测量则测量，不可测量则估计）

Step2：基于 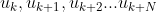进行最优化

Step3：只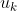取 (只选取 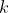时刻作为预测结果，因为预测存在局限性)

以及代价函数、预测区间等相关概念。

这一篇开始推导MPC数学模型，公式比较多。

DR_CAN的视频：【MPC模型预测控制器】2_最优化数学建模推导

---

1.最优化的方法之一：二次规划 Quadratic Programming

一般形式：

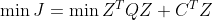
（包含两部分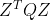：——二次型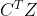，——线性）

若 𝑄 为对角矩阵，即  ，则转为最小二乘问题

如想了解更多有关二次规划的问题，可以参考这篇博客：

二次规划问题和MATLAB函数quadprog的使用

2.最优化建模数学推导

2.1系统的状态空间表达式

一个离散系统的状态方程：

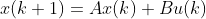
 其中 为状态向量， 为输入向量。

在 k 时刻：

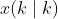  表示在k时刻预测 k 时刻的系统状态，

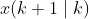表示在k时刻预测 k＋1 时刻的系统状态，

...

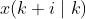
表示在k时刻预测 k＋N 时刻的系统状态。

表示在k时刻预测 k 时刻的输入，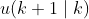

表示在k时刻预测 k+1 时刻的输入，

...

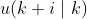
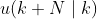表示在k时刻预测 k+N 时刻的输入。

即前面的 k 表示预测对象，后面的 k 表示在 k 时刻的预测。

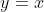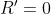为简化分析，假设系统输出方程： ，参考值 ，则误差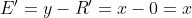

2.2代价函数

依据上一篇博客给出的代价函数表达式

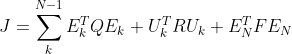
可得：

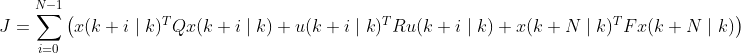
即：代价函数 = 误差加权和 + 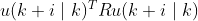输入加权和 + 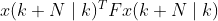终端误差。

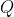其中 和 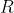为权重系数矩阵且均为对角矩阵，最优化的目标是最小化代价，即 .
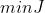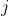的表达式中有两个变量（输入 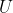和状态 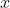），相比于二次规划一般形式多了一个变量。由于控制目标为控制输入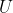，因此要消去变量 .

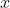2.3MPC数学模型推导

（个人理解：MPC目标为实现最优，也就是代价最小，数学形式即为代价函数的最小化，因此MPC公式推导主要是代价函数的推导和化简）

将状态变量用输入变量表示：

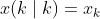为初始条件

将上式整理后可得：

令

， 

注意 为向量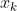， 为初始状态。 中的0代表零矩阵，而非数值0。

则

将代价函数展开：

 令

 则

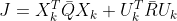
将 代入上式，消去变量 并化简：

因为 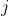 是一个 1×1 矩阵（ 和 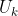均为 n×1 矩阵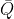， 和 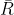均为 n×n 矩阵），因此实际上是一个数（至于为什么，可以参考线性代数中矩阵相乘相关内容），则 .

由于矩阵 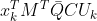和 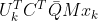互为转置且均为数值，则数值相等，即：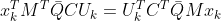

令

则

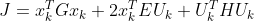
上式就是最终推导结果，符合二次规划的一般形式。其中 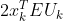 为线性部分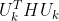， 为二次型部分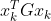， 表示初始状态，不影响最优化。

以上就是MPC数学模型推导过程，利用这个模型可以对系统进行最优化和模型预测控制设计。

（码了那么多公式，对 Latex 也越来越熟了...)