一 原问题描述

BST - POJ 2309 - Virtual Judgehttps://vjudge.net/problem/POJ-2309

二 输入和输出

1 输入

第 1 行包含一个整数 N，表示查询的数量。在接下来的 N 行中，每行都包含一个数字，表示根号为 X 的子树。

2 输出

共 N 行，其中第 i 行包含第 i 个查询的答案。

三 输入和输出样例

1 输入样例

2

8

10

2 输出样例

1 15

9 11

四 分析

本问题规律可循，若 n 是奇数，那么必然是叶子节点，最大数和最小数都是它自己。否则求 n 所在的层次（倒数的层数，底层为 0），它的层数就是 n 的二进制表示中从低位开始第1个1所在的位置 i（最后一个非0位），例如 6 的二级制为110，从低位开始第1个1的位置是1，因此 6在第1层；12的二进制是1100，从低位开始第1个1的位置是2，因此12在第2层，如下图所示。

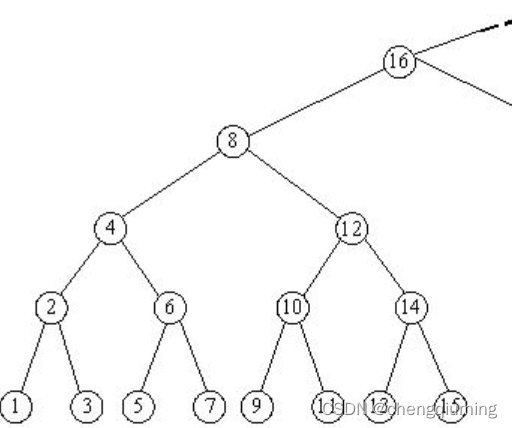
i 的值即为层数，可得到 n 的左右子树各有 k = 2^i-1个节点，那么最小数是 n-k，最大数是n+k，那么怎么求 2^i呢？

实际上，想得到最后一个非 0 位，只需先将原数取反后加1，此时除了最后一个非 0 位，其他位均与原数相反，直接与原数按位与运算即可得到最后一个非0位。

五 算法设计

1 求解logbit(n)=n&(-n)。

2 让 看= lowbit(n)-1,输出最小数 n-k，最大数 n+k。

六 代码

package poj2309;
 
import java.util.Scanner;
 
public class Poj2309 {
    static int lowbit(int n) {
        return n & (-n);
    }
 
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int T, n, k;
        T = scanner.nextInt();
        while (T-- > 0) {
            n = scanner.nextInt();
            k = lowbit(n) - 1;
            System.out.println((n - k) + " " + (n + k));
        }
    }
}

七 测试

绿色为输入，白色为输出