高精度

高精度加法

791
给定两个正整数（不含前导 0），计算它们的和。

输入格式
共两行，每行包含一个整数。

输出格式
共一行，包含所求的和。

数据范围
1≤整数长度≤100000
输入样例：
12
23
输出样例：
35
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

#include 
#include 
using namespace std;
// C = A + B
vector<int> add(vector<int> &A,vector<int> &B)  // 引用：提升效率，不加引用需要拷贝
{
    vector<int> C;
    int t = 0;  //上一次进位,最终用t来存储最终结果
    for(int i = 0; i < A.size()|| i < B.size();i++)
    {
        if(i < A.size()) t+=A[i];  //从上一次进位的基础上累加
        if(i < B.size()) t+=B[i];
        //t表示该位上的总的结构，结果vector中需要插入的是模10后的余数
        C.push_back(t%10);
        t /= 10; //用于下一次累加
    }
    if(t) C.push_back(t);
    return C;
    
}

int main()
{
    string a,b; //用字符串读 123456
    vector<int> A,B,C;  //存储到vector容器中去
    cin>>a>>b;
    //逆序
    for(int i = a.size()-1;i>=0;i--) A.push_back(a[i]-'0'); // A 654321 
    for(int i = b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
    C = add(A,B);
    //倒着输出，先输出最高位，再输出次高位
    for(int i =C.size()-1;i>=0;i--) printf("%d",C[i]);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

高精度减法

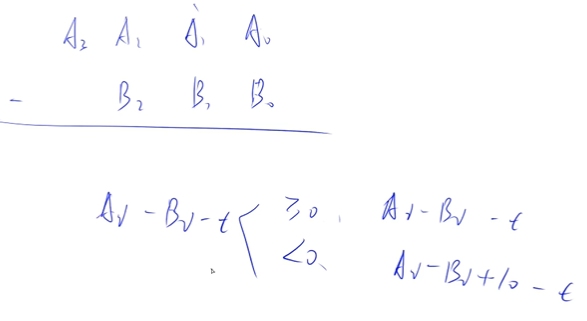
792
给定两个正整数（不含前导 0），计算它们的差，计算结果可能为负数。

输入格式
共两行，每行包含一个整数。

输出格式
共一行，包含所求的差。

数据范围
1≤整数长度≤105
输入样例：
32
11
输出样例：
21
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

#include 
#include 
using namespace std;
//判断是否A>=B
bool cmp(vector<int> &A,vector<int> &B)
{
    //首先判断位数 判断大小只要不等直接返回A.size()>B.size()
    if(A.size()!= B.size()) return A.size()>B.size();
    // i--时，第二个判断条件为>=,i++时,第二个条件可以为 <
    for(int i = A.size()-1;i>=0;i--)
        if(A[i]!=B[i])
                //判断大小只要不等直接返回A.size()>B.size()
                return A[i]>B[i];
    return true;
}
vector<int> sub(vector<int> &A,vector<int> &B)
{
    vector<int> C;
    for(int t = 0,i = 0;i < A.size();i++)
    {
        //t 上次运算的借位
        t = A[i] - t;
        if(i < B.size()) t -=B[i];
        // t>=0 -- t  t<0 ---t+10
        C.push_back((t+10)%10);
        if(t < 0) t = 1;
        else t = 0;
    }
    //清空前置0，如果本身是0，不进行前导0 即C.size()>1
    while(C.size()>1 && C.back() == 0) C.pop_back();

    return C;
}

int main()
{
    string a,b;
    vector<int> A,B,C;
    cin>>a>>b;
    for(int i = a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
    for(int i  =b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
    if(cmp(A,B))
    {
        C = sub(A,B);
        
    }
    else
    {
        C = sub(B,A);
        printf("-");
    }
    for(int i =C.size()-1;i>=0;i--) printf("%d",C[i]);


    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

高精度乘法

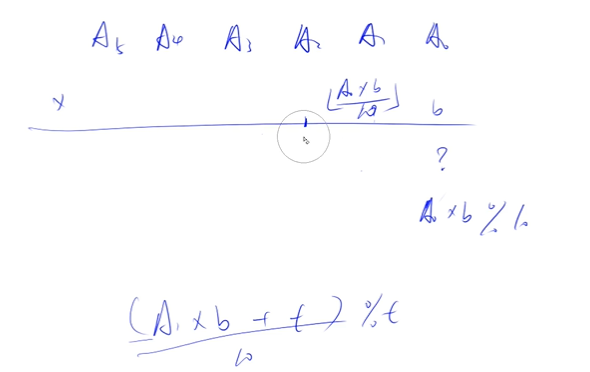
793
给定两个非负整数（不含前导 0） A 和 B，请你计算 A×B 的值。

输入格式
共两行，第一行包含整数 A，第二行包含整数 B。

输出格式
共一行，包含 A×B 的值。

数据范围
1≤A的长度≤100000,
0≤B≤10000
输入样例：
2
3
输出样例：
6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

#include 
#include 
using namespace std;


//C = A * b
vector<int> mul(vector<int> &A,int b)
{
    vector<int> C;
    int t = 0; //进位
    //需要判断两种情况 A的位数没有处理完  或者  进位没有处理完
    for(int i = 0;i<A.size()||t;i++)
    {
        if(i<A.size()) t += A[i]*b;
        //插入模10后的余数
        C.push_back(t%10);
        t/=10;
    }
    while(C.size() > 1&& C.back() == 0) C.pop_back();
    return C;
}

/*
如果将for循环两个条件拆开，可以采用这种写法，但和在一块写效果更好
vector mul(vector &a,int &b)
{
    int t = 0;
    for(int i = 0;i < a.size();i++)
    {
        t += a[i]*b;
        c.push_back(t%10);
        t /=10;
    }
    while(t) 
    {
        c.push_back(t%10);
        t /= 10;
    }
    while(c.size() > 1 && c.back() == 0) c.pop_back();
    return c;
}

*/

int main()
{
    string a;
    vector<int> A;
    int b;
    cin>>a>>b;
    for(int i = a.size()-1;i>=0;i--)
    {
        A.push_back(a[i]-'0');
    }
    // for(int i =A.size()-1;i>=0;i--) printf("%d",A[i]);
    auto c = mul(A,b);
    for(int i =c.size()-1;i>=0;i--) 
    printf("%d",c[i]);
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

高精度除法

举例

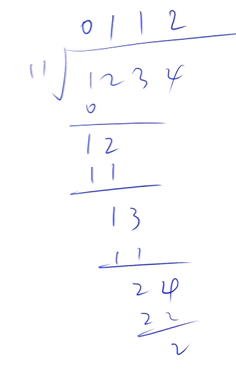
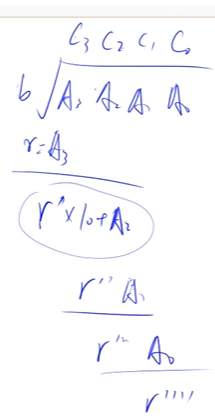
794
给定两个非负整数（不含前导 0） A，B，请你计算 A/B 的商和余数。

输入格式
共两行，第一行包含整数 A，第二行包含整数 B。

输出格式
共两行，第一行输出所求的商，第二行输出所求余数。

数据范围
1≤A的长度≤100000,
1≤B≤10000,
B 一定不为 0
输入样例：
7
2
输出样例：
3
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

#include 
#include 
#include 
using namespace std;


//A/b 商是C，余数是r,r通过引用传递
vector<int> div(vector<int> &A,int b,int &r)
{
    vector<int> C;
    r = 0;  //r代表上一次的余数
    //除法从最高位开始看；注意i++还是i--
    for(int i = A.size()-1;i>=0;i--)
    {
        //r * 10 把r整体向高位移动一位，将最后一位空出来
        r = r * 10 + A[i];
        //从头开始除，r/b不会是两位数
        C.push_back(r / b);
        r %= b;
    }
    //C中最低位存的是最高位，最高位存的是最低位
    reverse(C.begin(),C.end());
    //前导0
    while(C.size() > 1 && C.back()==0) C.pop_back();
    return C;

}

int main()
{
    string a;
    vector<int> A;
    int b;
    cin>>a>>b;
    for(int i = a.size()-1;i>=0;i--)
    {
        A.push_back(a[i]-'0');
    }
    int r;
    auto c = div(A,b,r);
    for(int i =c.size()-1;i>=0;i--) 
    printf("%d",c[i]);
    cout<<endl<<r<<endl;
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

理解

代码背的不是字母，背的是思路

---

前缀和

一维前缀和

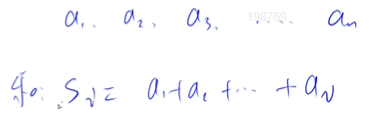
S0= 0

作用：快速求出原数组中一段的和

注意1:此处为S_r - S_l-1

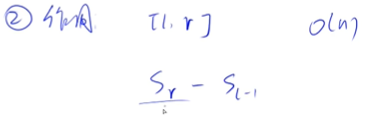
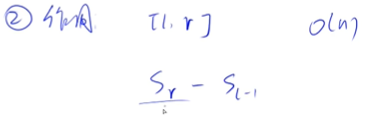
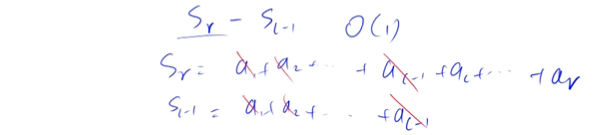
**注意2： 下标从1开始：**定义S0 = 0

好处：主要是处理边界，统一处理所有情况；不需要进行特判

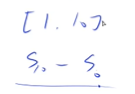
输入一个长度为 n 的整数序列。

接下来再输入 m 个询问，每个询问输入一对 l,r。

对于每个询问，输出原序列中从第 l 个数到第 r 个数的和。

输入格式
第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数数列。

接下来 m 行，每行包含两个整数 l 和 r，表示一个询问的区间范围。

输出格式
共 m 行，每行输出一个询问的结果。

数据范围
1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000
输入样例：
5 3
2 1 3 6 4
1 2
1 3
2 4
输出样例：
3
6
10
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

#include 
using namespace std;
//统一表示数组长度，避免每次定义数组声明长度
const int N = 100010;
int n,m;
int a[N],s[N];
int main()
{
    scanf("%d%d",&n,&m);
    //对于数组输入来说，用for比用while更加方便
    for(int i = 1;i<=n;i++) scanf("%d",&a[i]);
    for(int i = 1;i<=n;i++) s[i] = s[i-1] + a[i];  //前缀和的初始化
    while(m--)
    {
        int l ,r;
        scanf("%d%d",&l,&r);
        printf("%d\n",s[r]-s[l-1]);  //区间和的计算
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

二维前缀和–求子矩阵中一部分和

求S_ij–四部分矩形组合:拆出来a_ij==>S_i-1,j S_i,j-1 S_i-1,j-1

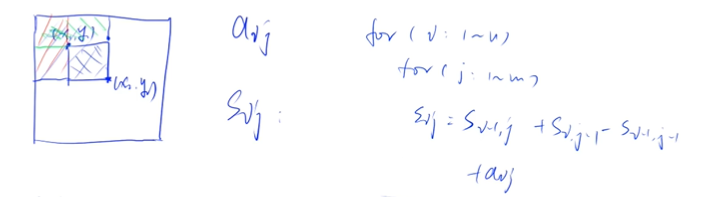
求子矩形的面积–四部分矩形组合

S_x2y2

X不变：X2，Y变：Y1-1

Y不变： Y2，X变：X1-1

S_x1-1,y2 S_x2,y1-1

S_x1-1,y1-1

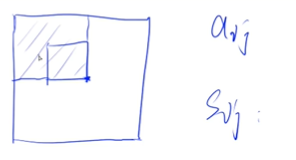
具体分析

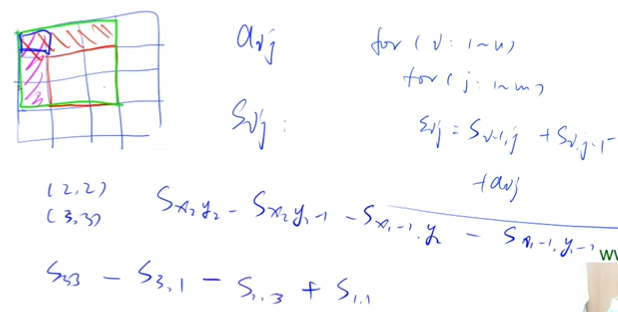
//796
输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式
第一行包含三个整数 n，m，q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含四个整数 x1,y1,x2,y2，表示一组询问。

输出格式
共 q 行，每行输出一个询问的结果。

数据范围
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000
输入样例：
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例：
17
27
21
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

#include 

const int N =1010;
int n,m,q;
int a[N][N],s[N][N];
int main()
{
    scanf("%d%d%d",&n,&m,&q);
    for(int i = 1;i<= n;i++)
        for(int j = 1;j<= m;j++)
            scanf("%d",&a[i][j]);
    for(int i = 1;i<=n;i++)
        for(int j = 1;j<=m;j++)
            s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1]+a[i][j]; //求前缀和
    while(q--)
    {
        int x1,y1,x2,y2;
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        printf("%d\n",s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]);  //算子矩阵的部分和
        
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

差分

一维差分

差分是前缀和的逆运算

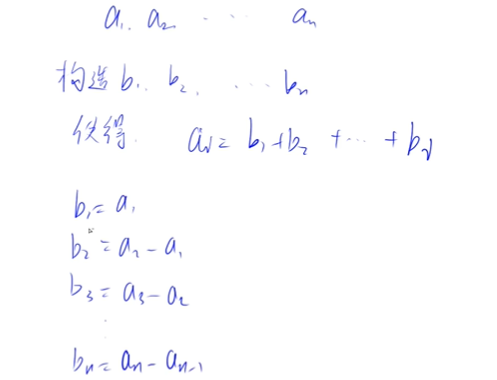
好处：对某个区间的数据加和减小了时间复杂度

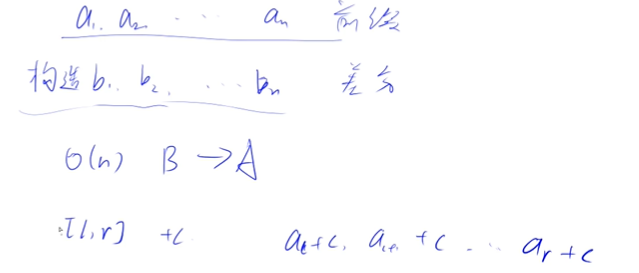
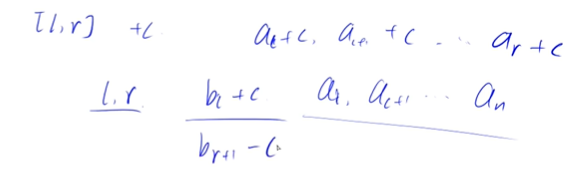
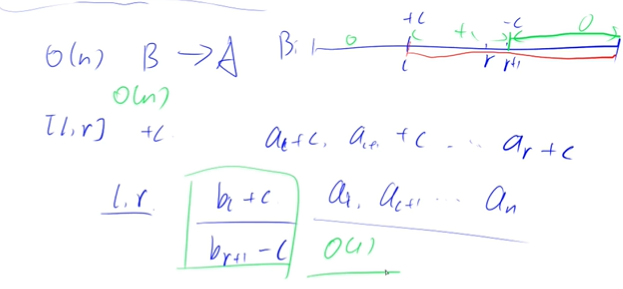
差分：

a[N],b[N]全部初始化为0，b[N]不需要单独构造，只需要在a[N]基础上进行增值的操作即可，即不存在构造函数

输入一个长度为 n 的整数序列。

接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r] 之间的每个数加上 c。

请你输出进行完所有操作后的序列。

输入格式
第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数序列。

接下来 m 行，每行包含三个整数 l，r，c，表示一个操作。

输出格式
共一行，包含 n 个整数，表示最终序列。

数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000
输入样例：
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例：
3 4 5 3 4 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

#include 

using namespace std;

const int N = 100010;

int n,m;
int a[N],b[N];

void insert(int l,int r,int c)
{
    b[l] += c;
    b[r+1] -= c;
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i = 1;i<=n;i++) scanf("%d",&a[i]);
    for(int i = 1;i<=n;i++ ) insert(i,i,a[i]);
    while(m--)
    {
        int l,r,c;
        scanf("%d%d%d",&l,&r,&c);
        insert(l,r,c);
    }
    for(int i = 1;i<=n;i++) b[i] +=b[i-1];  //构造前缀和
    for(int i = 1;i<=n;i++) printf("%d ",b[i]);
    return 0;    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

二维差分

差分都不考虑人工构造，只考虑如何更新

输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c。

请你将进行完所有操作后的矩阵输出。

输入格式
第一行包含整数 n,m,q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含 5 个整数 x1,y1,x2,y2,c，表示一个操作。

输出格式
共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例：
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例：
2 3 4 1
4 3 4 1
2 2 2 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

#include 

using namespace std;

const int N = 1010;
int a[N][N], b[N][N];
int n,m,q;

void insert(int x1,int y1,int x2 ,int y2,int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}


int main()
{
    scanf("%d%d%d",&n,&m,&q);
    for(int i = 1;i<=n;i++)
        for(int j = 1;j<=m;j++)
            scanf("%d",&a[i][j]);
    for(int i = 1;i<=n;i++)
        for(int j = 1;j <= m;j++ )
            insert(i,j,i,j,a[i][j]);
    while(q--)
    {
        int x1,y1,x2,y2,c;
        //输入数据不要弄错顺序
        //结果与预期不同，先检查输入有没有错误
        scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&c);
        insert(x1,y1,x2,y2,c);
    }
    for(int i = 1;i<=n;i++)
        for(int j = 1;j<=m;j++)
            b[i][j] += b[i-1][j]+b[i][j-1]-b[i-1][j-1];
    for(int i = 1;i<=n;i++)
    {
        for(int j = 1;j<=m;j++)
            printf("%d ",b[i][j]);
        printf("\n");
    }

    return 0;
    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47