共n级台阶，每次可以上1级或2级台阶，有多少种上法？

CSDN每日一练题目

• 2022-08-02日CSDN每日一练中等难度题目。
• 题目要求 1 <= N <= 50，当输入N后在一秒钟之内计算出结果。
• 题目类型：递归、循环
  

做答过程

测试示例：

• n = 3 , 正确结果为 3
• n = 4 , 正确结果为 5
• n = 5 , 正确结果为 8
• n = 6 , 正确结果为13

1、普通递归法

• 刚开始思路不是很明确，就随便写写，写出个递归，但是当N较大时，计算效率极低。

代码

class Main {
    public static void main(String[] args) {
        System.out.println(System.currentTimeMillis());
        int n = 50;
        int result = solution(n);

        System.out.println(result);
        System.out.println(System.currentTimeMillis());

    }

    public static int solution(int n) {
        int result = 0;

        if (n >= 1 && n <= 2){
            result = n;
        } else {
            result = solution(n -1) + solution(n - 2);
        }

        return result;
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

结果

• 因为计算时间较长，官方没有说明计算结果是否正确，只是说明超时。

2、递归优化

• 第一种递归效率很低，所以想着优化递归。
• 优化思路：因为只能走1级或2级台阶，那么可以先确定走1级和2级总的搭配种类，举例说明：如共5级台阶，那么可以先确定1和2的搭配方式有：5次1级、3次1级和1次2级、1次1级和2次2级。先不管第几步做1级或2级，基本的搭配就这三种，先确定这三种搭配，再对每种搭配进行排序即可。

代码

class Main {
    public static void main(String[] args) {
        System.out.println(System.currentTimeMillis());
        int n = 20;
        int result = solution(n);

        System.out.println(result);
        System.out.println(System.currentTimeMillis());

    }

    public static int solution(int n) {
        int result = 0;
        for (int oneNum = n; oneNum >= 0; oneNum--) {
            if ((n - oneNum) % 2 == 0) {
                result += countNum(oneNum, (n - oneNum) / 2);
            }
        }
        return result;
    }

    public static int countNum(int oneNum, int twoNum) {
        if (oneNum == 0 || twoNum == 0) {
            return 1;
        } else if (oneNum == 1 || twoNum == 1) {
            return oneNum + twoNum;
        }
        int total = 0;

        for (int i = 0; i <= oneNum; i++) {
            if (oneNum - i == 0) {
                total += 1;
            } else {
                total += countNum(oneNum - i, twoNum - 1);
            }
        }

        return total;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

结果

• 虽然优化有一定的效果，但当N较大时依然很慢，所以这种写法还不是答案。

3、使用排列组合公式、并优化

• 在第二种写法时，递归的时候，就已经觉得是高中时学的排列组合问题了，由于一时没想起来公式是啥，就没有去实践。但结果仍然不对，那就只能去思考使用高中的排列组合公式能否可行。

• 排列公式：本题中不适用排列公式

• 

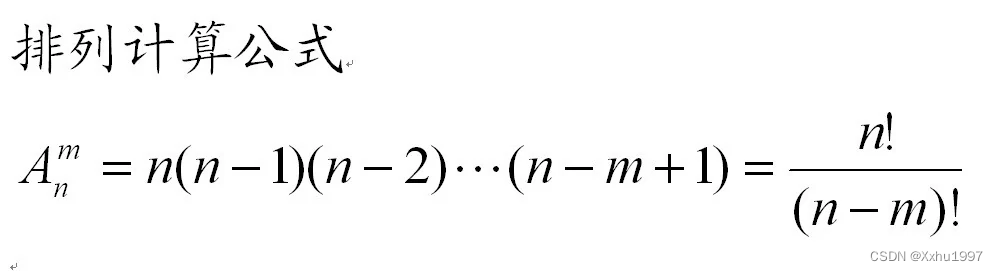
• 组合公式：其中阶乘式比较适合使用，转化为本题，公式中n就是走1级次数和走2级次数的总和，m可以是1级次数或2级次数，结果相同。

• 

基本排列组合

class Main {
    public static void main(String[] args) {
        System.out.println(System.currentTimeMillis());
        int n = 20;
        int result = solution(n);

        System.out.println(result);
        System.out.println(System.currentTimeMillis());

    }

    public static int solution(int n) {
        int result = 0;
        for (int oneNum = n; oneNum >= 0; oneNum--) {
            if ((n - oneNum) % 2 == 0) {
                result += countNum(oneNum, (n - oneNum) / 2);
            }
        }
        return result;
    }
    public static int countNum(int oneNum, int twoNum) {
        if (oneNum == 0 || twoNum == 0) {
            return 1;
        } else if (oneNum == 1 || twoNum == 1) {
            return oneNum + twoNum;
        }
        int total = 0;
        int top = 1;
        for (int i = oneNum + twoNum; i > 1; i--) {
            top *= i;
        }

        int down = 1;
        for (int i = oneNum; i > 1; i--) {
            down *= i;
        }
        for (int i = twoNum; i > 1; i--) {
            down *= i;
        }
        total = top / down;

        return total;
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

结果

• 使用此代码测试，当N过大时，计算无法正常执行，会报错，原因是当N过大时，阶乘后数字过大，超出类型存储数字范围，导致数字变成0，最终导致分母为0计算出错。

优化公式计算逻辑

• 优化思路：
• 1、先对公式进行约分，减小阶乘数值
• 2、m选取较小的数字，如果走1级台阶的次数小，就将1级台阶次数置为m，反之则是2级台阶次数。

class Main {
    public static void main(String[] args) {
        System.out.println(System.currentTimeMillis());
        int n = 20;
        int result = solution(n);

        System.out.println(result);
        System.out.println(System.currentTimeMillis());

    }

    public static int solution(int n) {
        int result = 0;
        for (int oneNum = n; oneNum >= 0; oneNum--) {
            if ((n - oneNum) % 2 == 0) {
                result += countNum(oneNum, (n - oneNum) / 2);
            }
        }
        return result;
    }

    public static int countNum(int oneNum, int twoNum) {
        if (oneNum == 0 || twoNum == 0) {
            return 1;
        } else if (oneNum == 1 || twoNum == 1) {
            return oneNum + twoNum;
        }
        int total = 0;
        int topMin = 1;
        int downMax = 1;
        if (oneNum > twoNum) {
            topMin = oneNum;
            downMax = twoNum;
        } else {
            topMin = twoNum;
            downMax = oneNum;
        }
        int top = 1;
        for (int i = oneNum + twoNum; i > topMin; i--) {
            top *= i;
        }

        int down = 1;
        for (int i = downMax; i > 1; i--) {
            down *= i;
        }
        total = top / down;

        return total;
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

总结

• 结果：很不幸，当天没有去认真回忆排列组合公式，导致没有写完优化后这种方案，最后没有提交结果，不知道最后的答案是否正确。
• 感悟：
• 1、很多问题用初中高中就能解决，可惜你都忘了。
• 2、有些问题不要死磕，该查查，能节省很多时间。
• 3、算法真难。-.-