一. 模板

(1) 拉链法
    int h[N], e[N], ne[N], idx;

    // 向哈希表中插入一个数
    void insert(int x)
    {
        int k = (x % N + N) % N;
        e[idx] = x;
        ne[idx] = h[k];
        h[k] = idx ++ ;
    }

    // 在哈希表中查询某个数是否存在
    bool find(int x)
    {
        int k = (x % N + N) % N;  // // c++中如果是负数 那他取模也是负的 所以 加N 再 %N 就一定是一个正数
        for (int i = h[k]; i != -1; i = ne[i])
            if (e[i] == x)
                return true;

        return false;
    }

(2) 开放寻址法
    int h[N];

    // 如果x在哈希表中，返回x的下标；如果x不在哈希表中，返回x应该插入的位置
    int find(int x)
    {
        int t = (x % N + N) % N;
        while (h[t] != null && h[t] != x)
        {
            t ++ ;
            if (t == N) t = 0;
        }
        return t;  // 如果这个位置是空的, 则返回的是他应该存储的位置
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

• 寻找大于 i 的最小的质数（确定N）

    for (int i = 1e5; i; ++i) {
        bool flag = true; // 判断是否为质数;
        for (int j = 2; j * j <= i; ++j) {  // 从2检测到i的一半，小于i/2不存在时，大于i/2肯定也不存在
            if (i % j == 0) {
                flag = false;  // 不为质数
                break;  
            }
        }
        if (flag) {  // 找到质数
            cout << i << endl;
            break;
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13

二. 总结

• 拉链法

• 开放寻址法
  
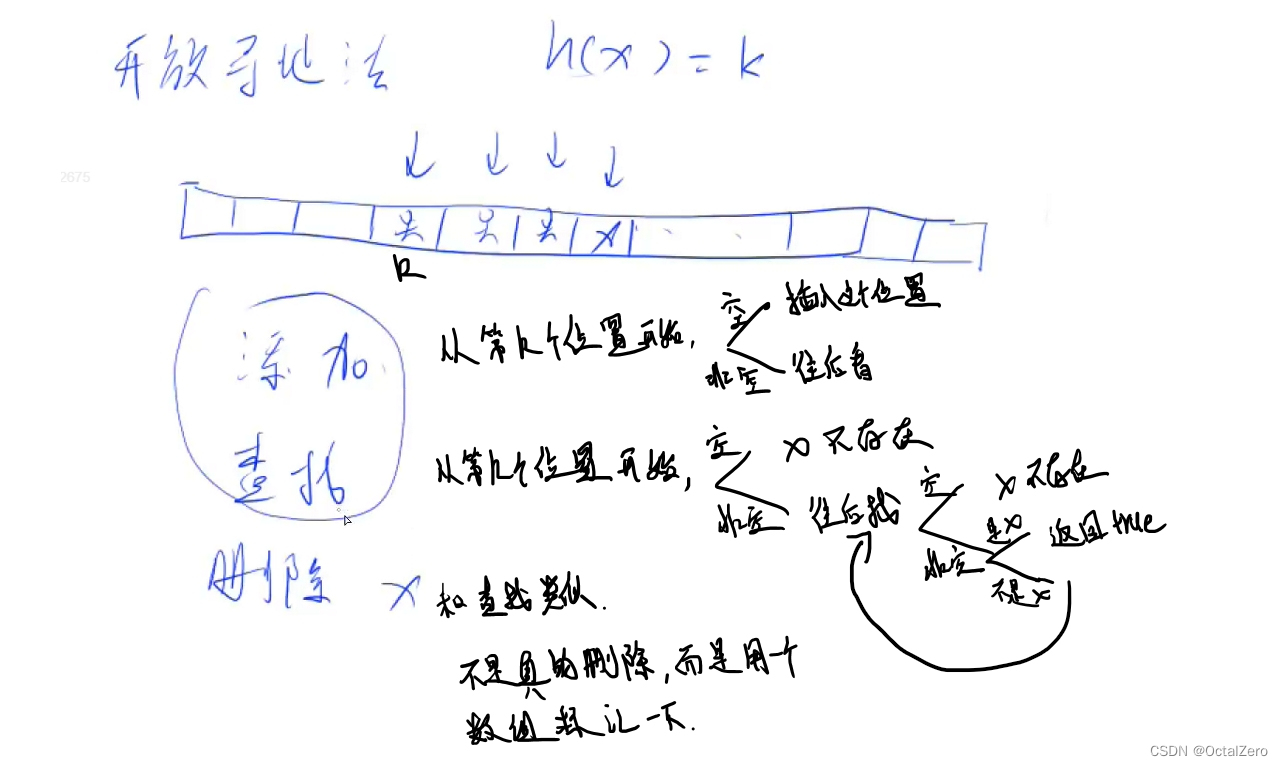
• 散列表原理
  

三. 例题

• 840. 模拟散列表

AC代码:

• 拉链法

#include 
#include 
using namespace std;

const int N = 100003;  // 取大于1e5的第一个质数，取质数冲突的概率最小

int h[N], e[N], ne[N], idx;

// 插入一个数  x
void insert(int x)
{
    int k = (x % N + N) % N; // 映射到hash表
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx++;
}


// 查询数 x 是否在集合中出现过
bool find(int x)
{
    int k = (x % N + N) % N;  // 映射到hash表
    for (int i = h[k]; i != -1; i = ne[i]) {  // 遍历链表
        if (e[i] == x)  return true;
    }
    
    return false;
}

int main()
{   
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0); 
    int n;
    cin >> n;
    
    memset(h, -1, sizeof h); // memset 按字节复制 -1 为 0XFF，复制后为0xFFFFFFFF也为-1
     
    char op;
    int x;
    while (n--) {
        cin >> op >> x;
        if (op == 'I') insert(x);
        else {
            if(find(x)) puts("Yes");
            else puts("No");
        }
    }
    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

• 开放寻址法

#include 
#include 

using namespace std;

//开放寻址法一般开 数据范围的 2~3倍, 这样大概率就没有冲突了
const int N = 2e5 + 3;        //大于数据范围的第一个质数
const int null = 0x3f3f3f3f;  //规定空指针为 null 0x3f3f3f3f

int h[N];

// 如果x在哈希表中，返回x的下标；如果x不在哈希表中，返回x应该插入的位置
int find(int x) {
    int t = (x % N + N) % N;
    while (h[t] != null && h[t] != x) {
        t++;
        if (t == N) {
            t = 0;
        }
    }
    return t;  // 如果这个位置是空的, 则返回的是他应该存储的位置
}

int main() {
    int n;
    cin >> n;

    memset(h, 0x3f, sizeof h);  //规定空指针为 0x3f3f3f3f

    while (n--) {
        string op;
        int x;
        cin >> op >> x;
        if (op == "I") {
            h[find(x)] = x;
        } else {
            if (h[find(x)] == null) {
                puts("No");
            } else {
                puts("Yes");
            }
        }
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45