LeetCode每日一题(2285. Maximum Total Importance of Roads)

You are given an integer n denoting the number of cities in a country. The cities are numbered from 0 to n - 1.

You are also given a 2D integer array roads where roads[i] = [ai, bi] denotes that there exists a bidirectional road connecting cities ai and bi.

You need to assign each city with an integer value from 1 to n, where each value can only be used once. The importance of a road is then defined as the sum of the values of the two cities it connects.

Return the maximum total importance of all roads possible after assigning the values optimally.

Example 1:

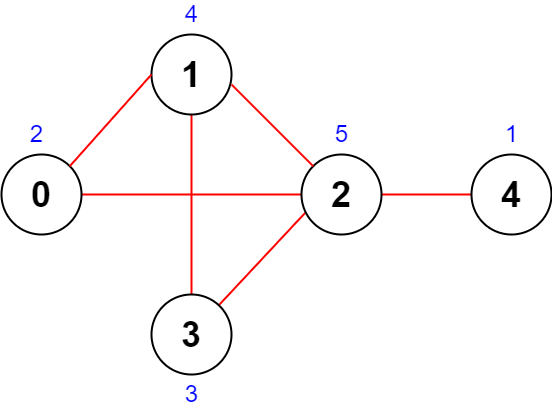
Input: n = 5, roads = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
Output: 43

Explanation: The figure above shows the country and the assigned values of [2,4,5,3,1].

• The road (0,1) has an importance of 2 + 4 = 6.
• The road (1,2) has an importance of 4 + 5 = 9.
• The road (2,3) has an importance of 5 + 3 = 8.
• The road (0,2) has an importance of 2 + 5 = 7.
• The road (1,3) has an importance of 4 + 3 = 7.
• The road (2,4) has an importance of 5 + 1 = 6.
  The total importance of all roads is 6 + 9 + 8 + 7 + 7 + 6 = 43.
  It can be shown that we cannot obtain a greater total importance than 43.

Example 2:

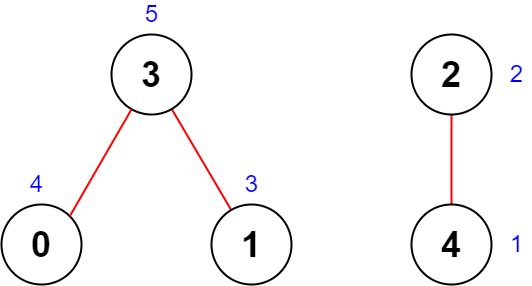
Input: n = 5, roads = [[0,3],[2,4],[1,3]]
Output: 20

Explanation: The figure above shows the country and the assigned values of [4,3,2,5,1].

• The road (0,3) has an importance of 4 + 5 = 9.
• The road (2,4) has an importance of 2 + 1 = 3.
• The road (1,3) has an importance of 3 + 5 = 8.
  The total importance of all roads is 9 + 3 + 8 = 20.
  It can be shown that we cannot obtain a greater total importance than 20.

Constraints:

• 2 <= n <= 5 * 104
• 1 <= roads.length <= 5 * 104
• roads[i].length == 2
• 0 <= ai, bi <= n - 1
• ai != bi
• There are no duplicate roads.

---

每个节点能为最终答案贡献 m * v 的 importance， m 代表与此节点连接的路的数量， v 代表的赋予此节点的值， 这样我们不难看出， 我们应该给 m 较大的节点赋予较大的值， 所以我们只需要统计每个节点锁连接的路的数量， 然后根据路的数量排序， 然后按顺序赋值求和就可以了

---

impl Solution {
    pub fn maximum_importance(n: i32, roads: Vec<Vec<i32>>) -> i64 {
        let mut counts = vec![0; n as usize];
        for road in roads {
            counts[road[0] as usize] += 1;
            counts[road[1] as usize] += 1;
        }
        counts.sort();
        counts
            .into_iter()
            .enumerate()
            .map(|(i, v)| v as i64 * (i as i64 + 1))
            .sum()
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15