-
深度学习之 10 卷积神经网络2
本文是接着上一篇深度学习之 10 卷积神经网络1_水w的博客-CSDN博客
目录
1 出现原因
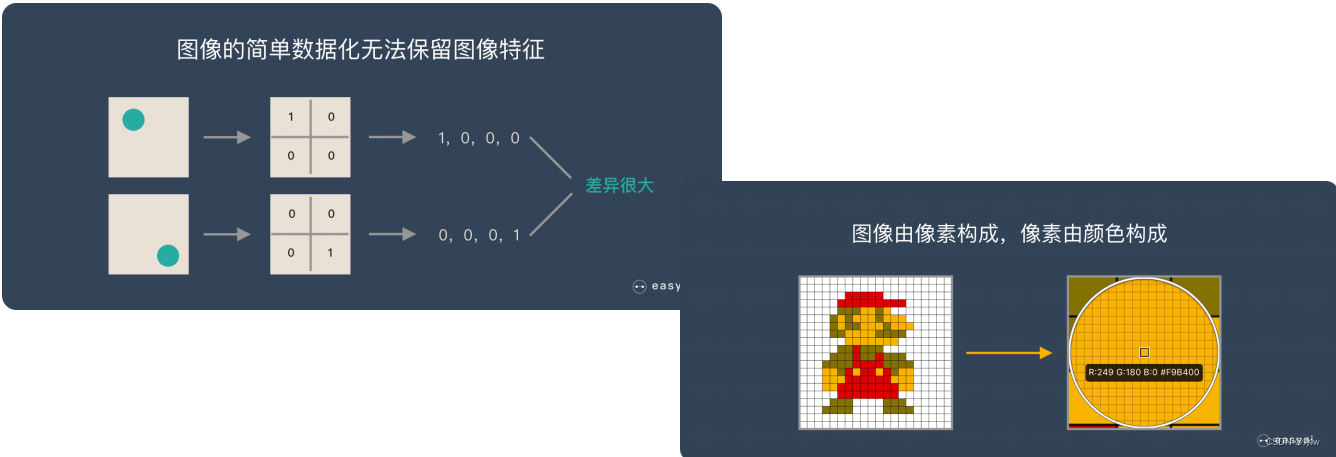
在 CNN 出现之前,图像对于人工智能来说是一个难题,有2个原因:
➢ 图像在数字化的过程中很难保留原有的特征,导致图像处理的准确率不高;
➢ 图像需要处理的数据量太大,导致成本很高,效率很低;

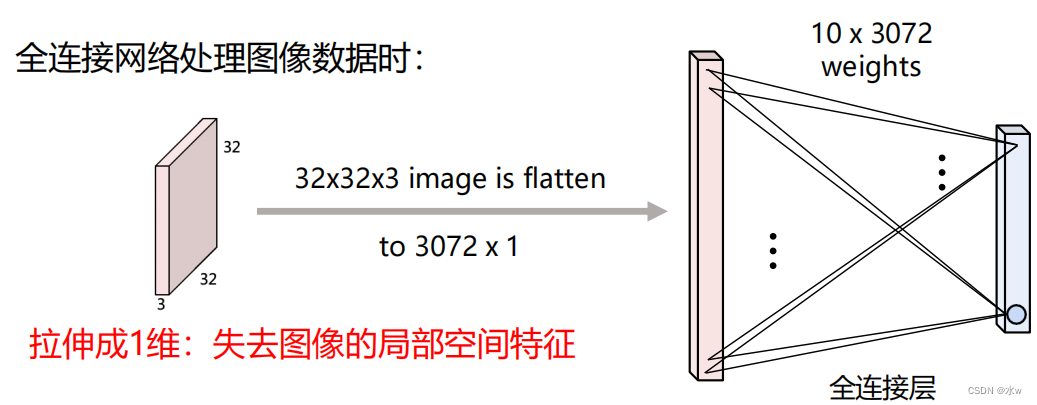
⚫ 全连接网络处理图像数据时,拉伸成1维:失去图像的局部空间特征。
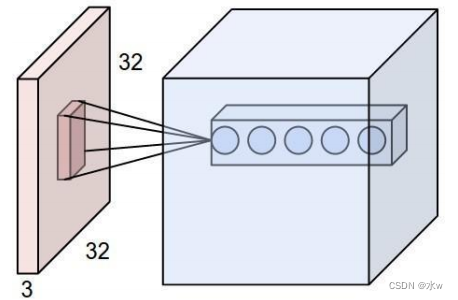
⚫ CNN 解决了这个问题:他用类似视觉的方式保留了图像的特征,当图像做翻转、旋转或者变换位置时,它也能有效的识别出来是类似的图像。
2 一般结构框架
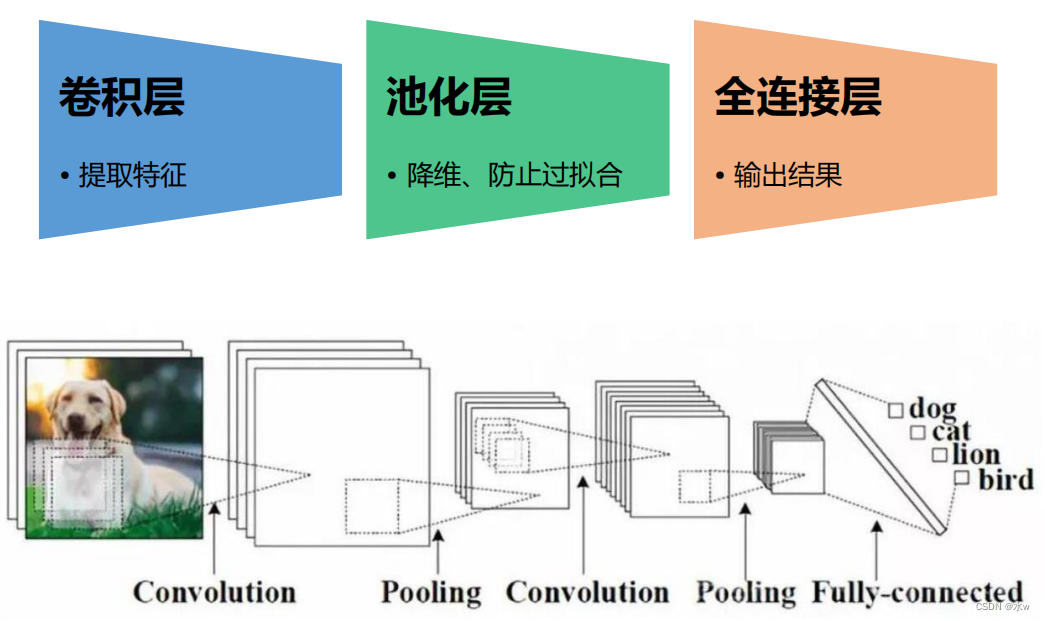
(1)一般结构框架:卷积层 ——利用卷积核提取特征
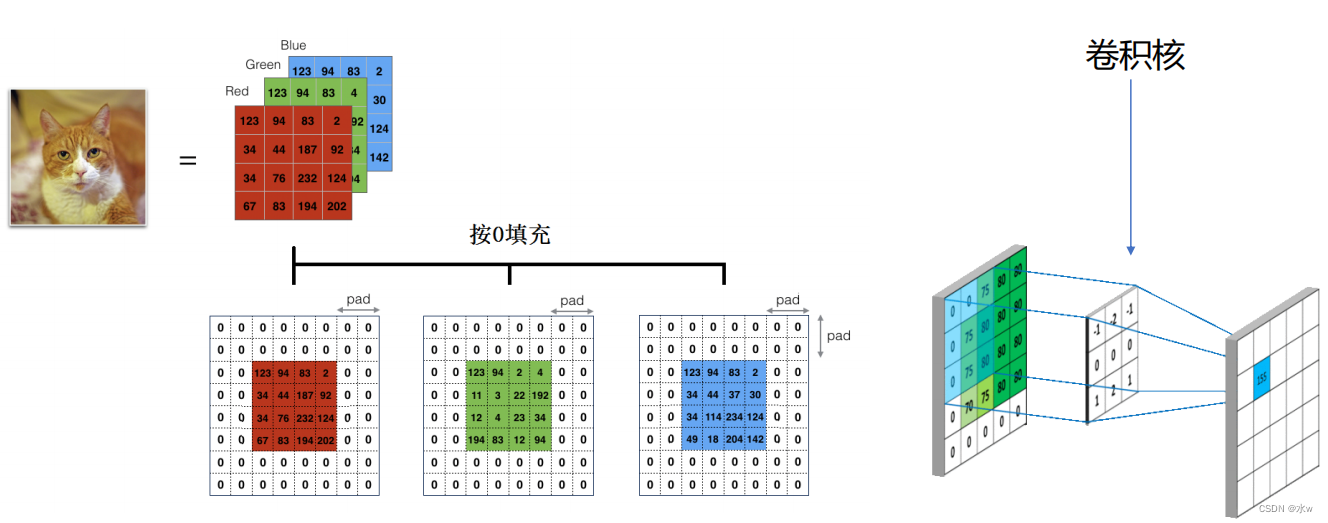
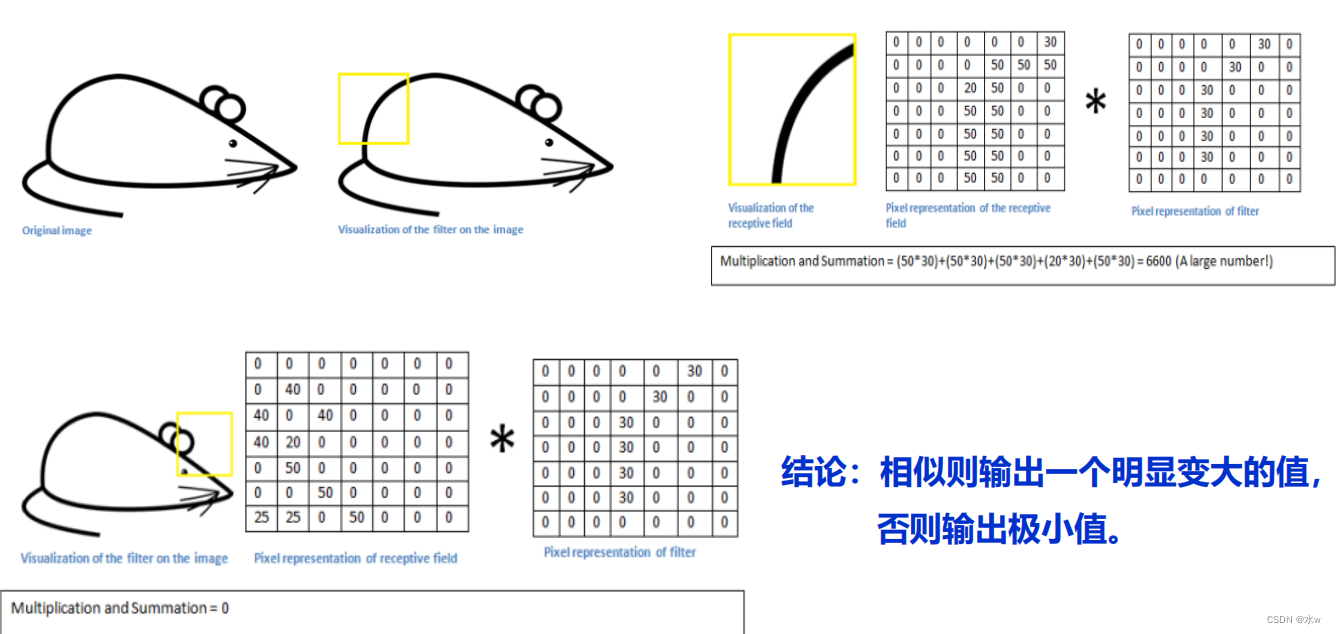
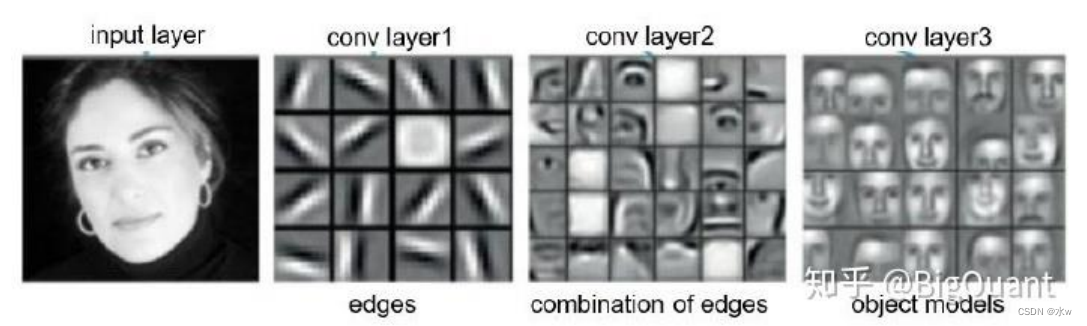
卷积核的本质:
第一层提取边缘,第二层将提取的边缘组合成形状,第三层提取的是明显的一些物体。
- 单个卷积核代表图像的某种简单特征。比如垂直边缘、水平边缘、颜色、纹理等。
- 所有卷积核加起来就好比是整张图像的特征提取器集合。
- 堆叠多层的卷积可以逐步提取更高层次、更复杂、更抽象、更泛化的特征。
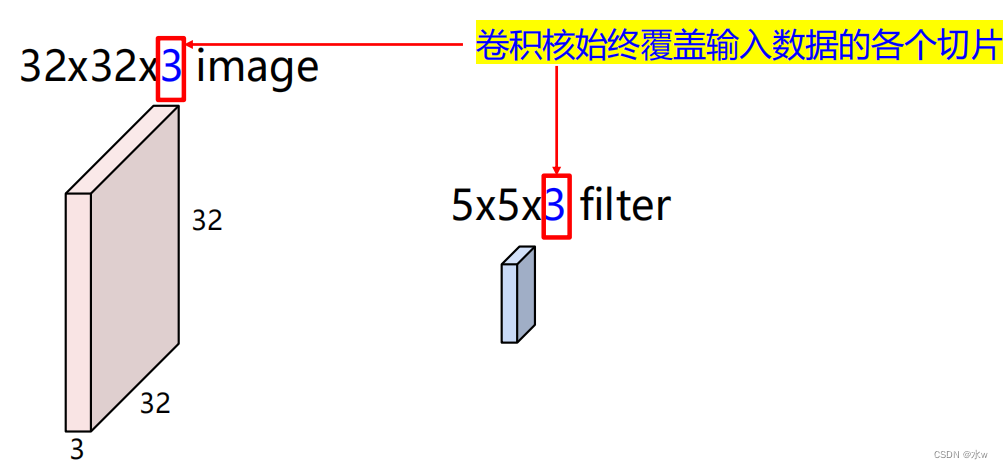
卷积核深度(通道数)应该与输入一致!
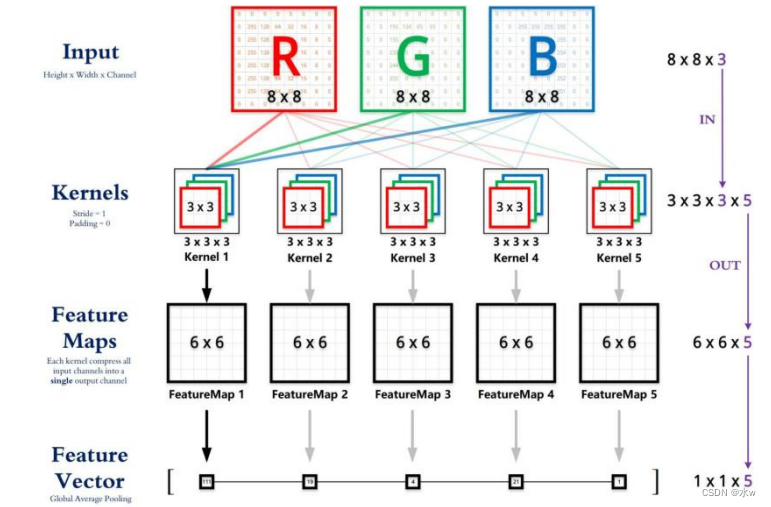
➢利用卷积核进行卷积计算,
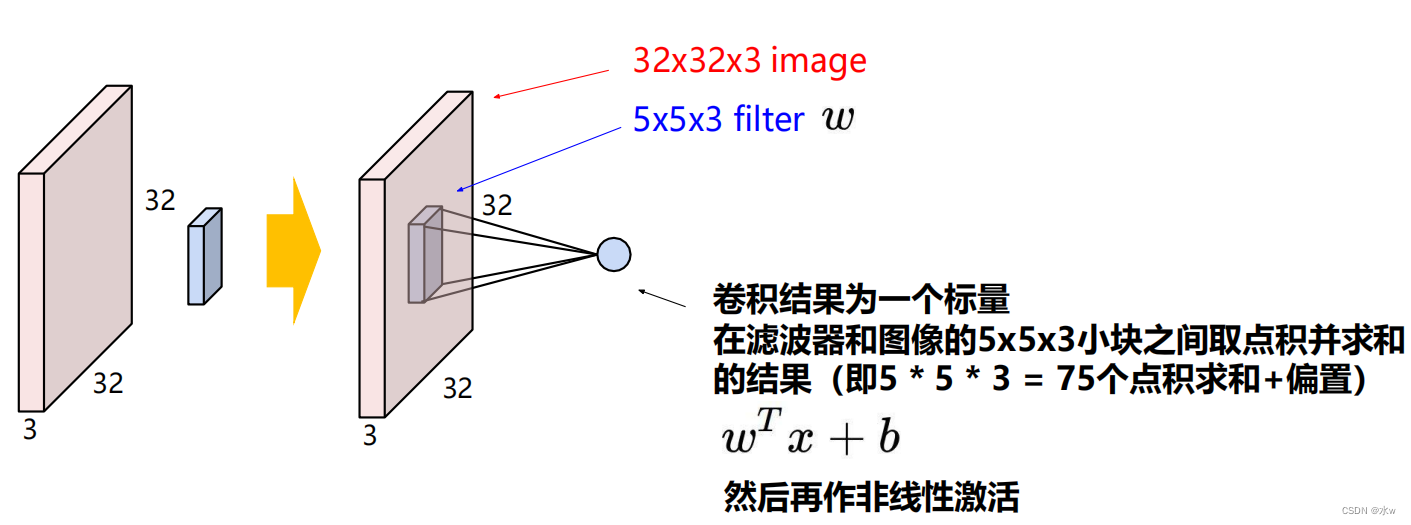
➢ 卷积结果,
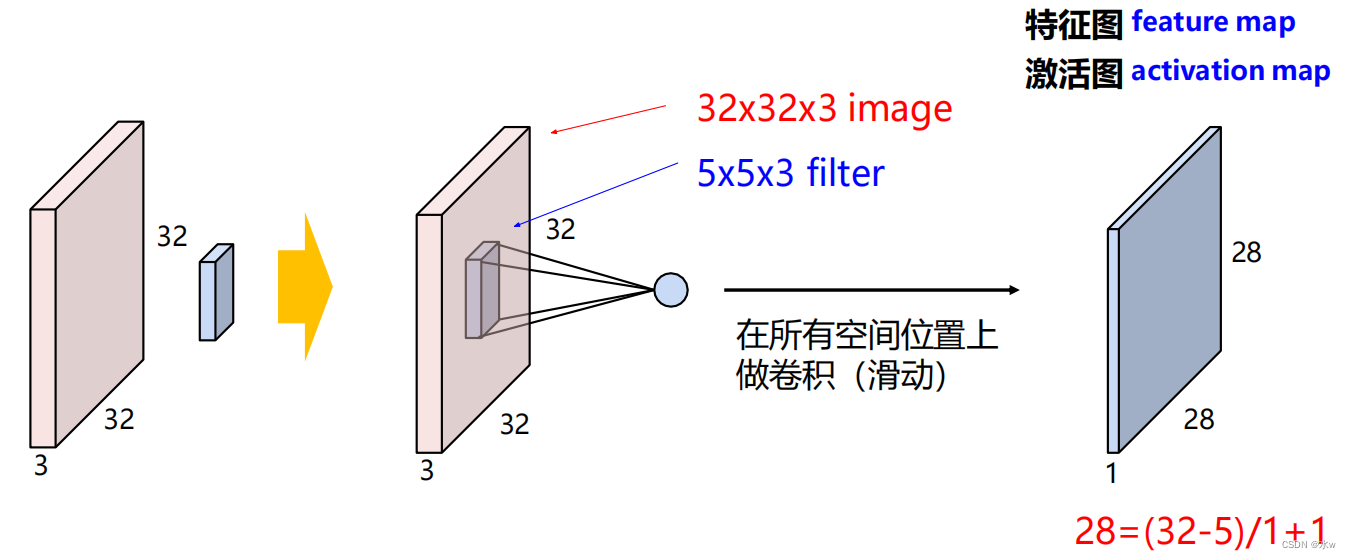
➢ 卷积结果:考虑多个滤波器
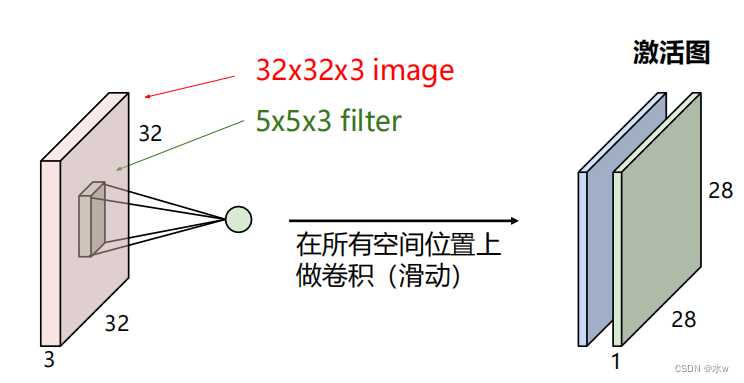
➢因此,如果我们有6个5x5x3的滤波器,我们将获得6个单独的激活图:
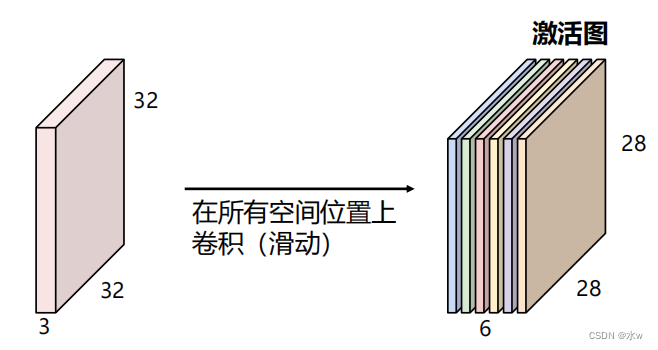
我们将它们堆叠起来,以获得尺寸为28x28x6的“新图片”!
⚫ 卷积层的输出的大小? --- 通道数➢ 某卷积层使用的卷积核的通道数等于该层输入数据的通道数➢ 某卷积层的输出通道数等于该层使用的卷积核的个数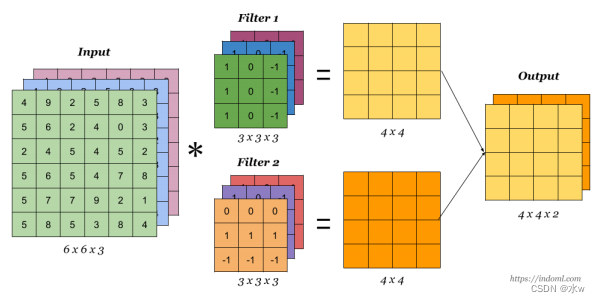 ⚫ 卷积层的输出的大小? --- 长/宽在实际中:常用零填充边框,保证输入输出尺寸相同 。 (N – K+2P) / stride + 1通常的情况是,卷积层步长设置为1,滤波器大小为KxK,则一般使用(K-1)/ 2个像素进行零填充(将在空间上保留大小)eg:输入图片大小: 32x32 x3 , 10个卷积核,大小为 5x5 x3,步长为 1, pad = 2。(1)输出图片大小: ( 32 - 5 +2* 2 )/ 1 +1 = 32 ,因此输出大小为 32x32x 10(2)这一层中的参数数量是多少? 每个卷积核具有 5 * 5 * 3 +1 = 76 个参数 (+1 for bias) => 76 * 10 = 760
⚫ 卷积层的输出的大小? --- 长/宽在实际中:常用零填充边框,保证输入输出尺寸相同 。 (N – K+2P) / stride + 1通常的情况是,卷积层步长设置为1,滤波器大小为KxK,则一般使用(K-1)/ 2个像素进行零填充(将在空间上保留大小)eg:输入图片大小: 32x32 x3 , 10个卷积核,大小为 5x5 x3,步长为 1, pad = 2。(1)输出图片大小: ( 32 - 5 +2* 2 )/ 1 +1 = 32 ,因此输出大小为 32x32x 10(2)这一层中的参数数量是多少? 每个卷积核具有 5 * 5 * 3 +1 = 76 个参数 (+1 for bias) => 76 * 10 = 760总结
给定一个卷积层,
⚫ 需要四个参数:✓ 卷积核数目 F✓ 卷积核大小 K✓ 步长 S✓ 零填充个数 P⚫ 输入图片大小为 𝑊 1 × 𝐻 1 × 𝐷 1;⚫ 经过卷积后输出大小为 𝑊 2 × 𝐻 2 × 𝐷 2 ,其中➢ 宽度:𝑊 2 = (𝑊 1 − 𝐾 + 2𝑃)Τ𝑆 + 1➢ 高度:𝐻 2 = (𝐻 1 − 𝐾 + 2𝑃)Τ𝑆 + 1➢通道数=卷积核数: 𝐷 2 = F⚫ 通过参数共享,每个滤波器引入 𝐾 ∗ 𝐾 ∗ 𝐷 1 + 1 个参数,因此一共有 𝐹 ∗ 𝐾 ∗ 𝐾 ∗ 𝐷 1 + F 个参数;⚫ 输出结果中,第 𝑑个切片(大小为 𝑊 2 × 𝐻 2 )是对输入通过第𝑑 个卷积核以步长 𝑆 做卷积然后加 上𝑏𝑖𝑎𝑠 的结果。特征图可视化
- 通过deconvolution,可以对feature map 进行可视化;
- 浅层layer学到的特征为简单的边缘、角点、 纹理、几何形状、表面等;
- 深层layer学到的特征则更为复杂抽象;
- 人工只能胜任简单卷积核的设计,如边缘;
- 卷积神经网络每层的卷积核权重是由数据驱动学习得来,不是人工设计的。
- 数据驱动卷积神经网络逐层学到由简单到复杂的特征(模式);
- 复杂模式是由简单模式组合而成;
- 不同的边缘->不同纹理->不同几何图形->不同的轮廓->不同的物体...
- 浅层模式的组合可以多种多样,使深层可以描述的模式也可以多种多样,所以具有很强的表
达能力。
(2)一般结构框架:池化层
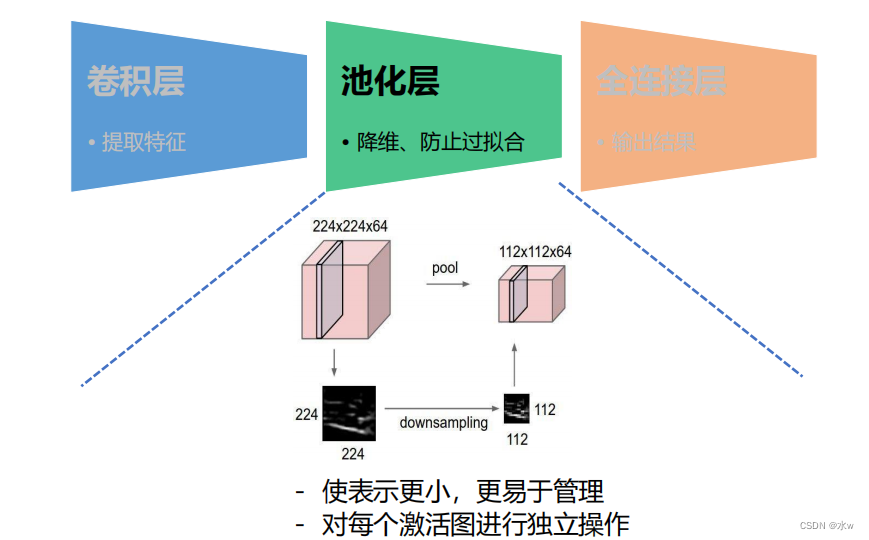
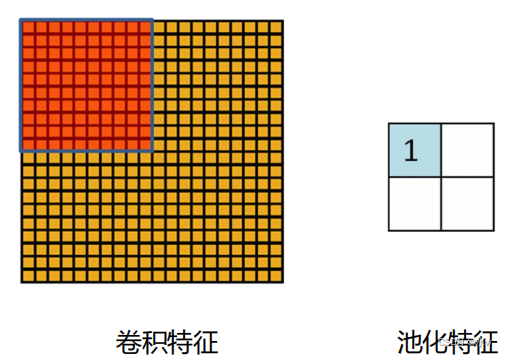
池化层(下采样)——数据降维,避免过拟合
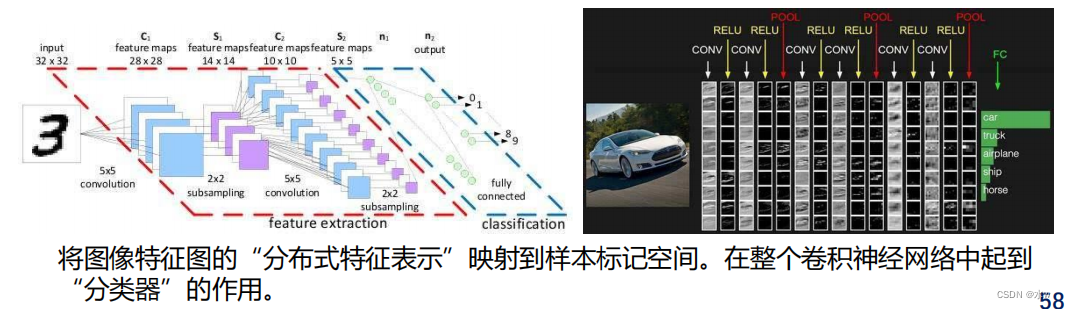
(3)一般结构框架:全连接层
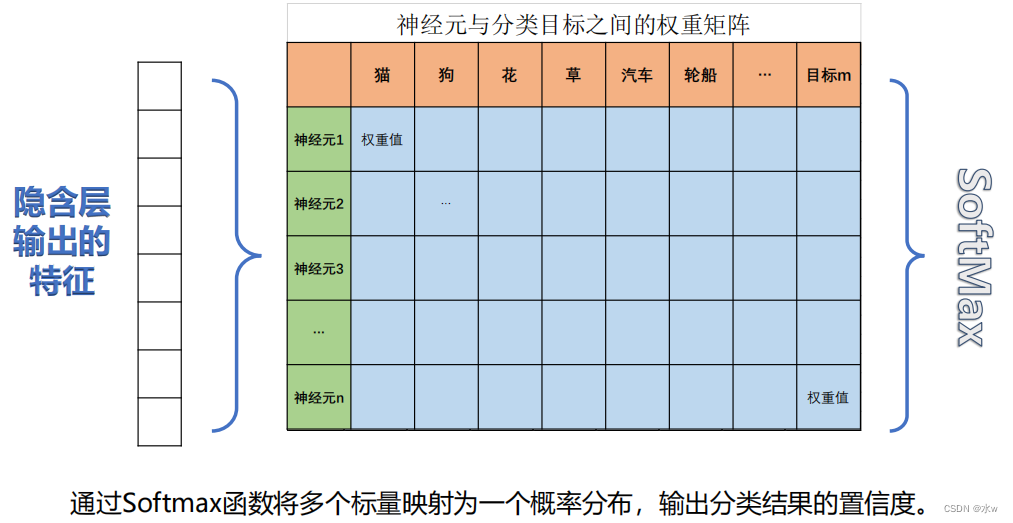
CNN卷积神经网络识别图像的过程
3 卷积神经网络擅长什么
以(多维)数组形式 出现的信号局部相关性强 的信号特征可以出现在任何位置的信号物体平移和变形不变的信号◼ 一维卷积网络:循序信号,文本• 文本、音乐、音频、演讲、时间序列◼ 二维卷积网络:图像,时频表示(语音和音频)• 目标检测、定位、识别◼ 三维卷积网络:视频,体积图像,断层扫描图像• 视频识别/理解• 生物医学图像分析• 高光谱图像分析 -
相关阅读:
Python—序列型数据操作实训
嘉为鲸翼·多云管理平台荣获信通院可信云技术服务最佳实践
H2/H∞半车悬架控制仿真分析
HC32L110 系列 M0 MCU 介绍和Win10下DAP-Link, ST-Link, J-Link方式的烧录
spring5.0源码解析 之 ConfigurationClassPostProcessor
企业数字化神经网络
qmt量化交易策略小白学习笔记第46期【qmt编程之期货行情数据--如何获取5档盘口行情、期货结算价与持仓量】
AI外呼机器人是怎么做到高效触客?效果如何?
软件测试技术之可用性测试之WhatsApp Web
JavaScript学习笔记
- 原文地址:https://blog.csdn.net/qq_45956730/article/details/126128553