-
《算法之美》读后感
最近读到一本好书,书名是Algorithms to Live By,有人翻译成《算法之美》,我认为更好的翻译是《用算法去生活》,因为它真的告诉我们如何将CS课程中学到的算法运用到日常生活中。算法不仅可以用在工程问题里,还可以用来优化生活中的许多决策。书中只涉及非常基础的算法,但相关的例子非常有启发性。
这篇是第一章——最佳停止。这个问题产生的算法可以帮助我们在招工,恋爱,卖房,停车,甚至赌博和偷窃(当然我们不宣传这种行为)中实现收益的最大化。
苏格拉底的麦田,招聘秘书,真命天子
我们大概都听过一个故事,说苏格拉底带他的徒弟们来到一片麦田,要求他们穿过麦田走到另一边,途中要捡一颗最大的麦子,只能捡一次,而且不能走回头路。一个徒弟很早就捡了一颗看起来很大的麦子,却错过了后面更大的麦子。另一个徒弟则一直犹豫不决,总觉得后面还会遇到更大的,最后两手空空走到了终点。如果我们要将苏格拉底想表达的哲学观点数学化,麦田问题就是一个典型的最佳停止问题。
最佳停止问题有一系列的变种,但最著名的要数秘书问题。这个问题等价于苏格拉底的麦田问题。假设我们公司要招聘一名秘书,预计会有 N 名应试者,我们需要对他们依次面试,每个人面试后需要立即做出录用或是拒绝的决定。被拒绝的人也不能被召回。决定录用某个人后,这个人会接受职位,我们也就不能考虑后面的应试者了。我们可以比较已面试的人中两两之间的优劣。怎样的策略才能最大化我们录取到最好的应试者的概率?
这里直接给出结论。最优策略是一个Look-and-Leap Rule:对于最开始一定比例 r 的应试者中,不管他们的表现如何出色,都必须拒绝,即我们的look阶段。从某个时刻开始,只要遇到比之前所有人都优秀的,就录取这个人,也就是take the leap。这个最优的比例 r=1/e ,因此这个策略也称为37%规则。证明不在这里赘述了,有兴趣的同学请移步乐乐老师的视频:
什么是爱情?怎么谈恋爱,才能有效的找到自己的真命天子?李永乐老师讲爱情数学www.bilibili.com/video/BV1Cb411A7pT正在上传…重新上传取消
这个策略有两个很优美的数学性质。第一,在这个策略下,录取到最优秀的人的概率恰好也是 1/e ,也就是我们一定会拒绝的比例。我们下面会提到,在某些秘书问题的变体中,这个对称性依然存在。第二,录取到最优秀的人的概率和面试者的人数无关,无论是有100个面试者还是100万个面试者,我们都有37%的概率录取到最优秀的人。
下面考虑秘书问题的一个变体——恋爱问题。同样,假设你会和若干个人依次恋爱,每次都要决定是否和这个人结婚,如何才能以最大的概率找到自己的真命天子(最合适自己的人)?和秘书问题不同的是,求婚有被拒绝的概率,而应试者不会拒绝offer。在这个条件下,Look-and-Leap依然是你的最优策略,只不过look的比例需要相应调小。举个例子,如果求婚的成功率是50%,那么最佳的比例 r 约为25%左右。如果失败,你依然向下一个至今遇到的最优秀的人求婚。这样,你和真命天子修成正果的概率同样约为25%左右,依然符合前面提到的对称性。
更进一步地,如果你还可以“回头看”,也就是挽回之前的感情,向当初没有求婚的人求婚呢?最优策略依旧是Look-and-Leap,然而我们可以有一个更长的look阶段,如果你谈完了N次恋爱还没有结婚,那就回头去在还没有拒绝你的人中,按照排名依次求婚,直到被接受为止。假如立即求婚的成功率是100%,“回头看”求婚的成功率是50%,那么最优的比例 r 是61%。同样,我们找到真命天子的概率也是61%。
再考虑另一个变体——完全信息假设。在之前的秘书问题中,我们假设可以对已经遇到的应试者进行两两比较,也就是说,我们知道每个人的相对名次。如果我们还知道每个人在群体中的percentile呢?比如说,我们计划面试10个人,但第一个应试者就在群体中超过97%的人,我们几乎可以确定之后不会遇到比他更优秀的应试者了,所以我们应该立即录用他,而不是把他放在look阶段而拒掉。事实上,在完全信息假设下,最优策略确实是没有look而直接leap,它被称为Threshold Rule:在还剩 M 个应试者没有面试时,只要当前的应试者超过约 (1−1/M)⋅100% percentile,我们就立即录用他。在这个策略下,我们有58%的概率录取到最优秀的人,略高于之前无信息假设下的秘书问题。
卖房问题
卖房问题是秘书问题在完全信息假设基础上的变体。当房产寻求出售的信息挂出后,我们会不断收到一些offer,每个买家会提议以某个价格买入。不同的是,这次我们的等待是有成本的——如果拒绝一个offer,我们就要等待下一个offer,同时继续支付房贷及其利息。然而好消息是,我们不仅可以量化我们的收益,还知道我们可能收到的offer的大致范围。具体地说,假设我们知道offer的报价是在一个下界 L 和一个上界 U 之间均匀分布的。
这个问题的最优策略也非常有意思。假设offer平均会以某个间隔不断地到来,我们可以根据这个间隔计算出等待每个offer的平均成本。最优策略说,我们可以根据这个平均成本以及报价的上下界确定一个预期价格,所有低于预期价格的offer一律拒绝,否则立即成交。这个结论的亮点在于,我们的决策规则不应该随着时间而变化;换句话说,即使收到了很多不尽如人意的offer,我们也不应该降低预期。(当然,如果这个趋势持续太久了,我们确实应该考虑修改一下对报价上下界的估计。)这就意味着,即使我们有机会“回头看”,我们也不应该这样做,去接受比预期低的结果。同样的结论适用于找工作。引用作者的话说:
In house selling and job hunting, even if it's possible to reconsider an earlier offer, and even if that offer is guaranteed to still be on the table, you should nonetheless never do so. If it wasn't above your threshold then, it won't be above your threshold now. What you've paid to keep searching is a sunk cost. Don't compromise, don't second-guess. And don't look back.
停车问题
寻找路边的停车位是很多人心中永远的痛。我们把停车问题理想化,假设有一条无限长的路,均匀分布着停车位,每个停车位已被占用的概率为 ρ ,且相互独立。我们从无穷远处驶来,沿着道路单向行驶,不能掉头,目标是最大化找到距离目标点最近的车位的概率。
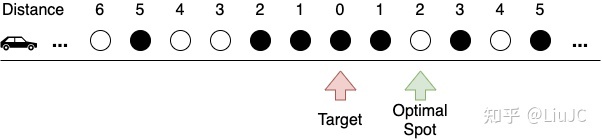
书中给的结论是,最优策略依然是Look-and-Leap:设置一个阈值 n ,从距离目标点还有 n 个车位时(也就是从编号为 n 的车位)开始,停在第一个空位置上。我们不做证明,只分析一下这个问题和秘书问题的异同。这两个问题sequential decision making,我们不能看到未来的选择,只能根据已有的信息做决策,而且不能反悔。对于停车问题,在Leap阶段我们会接受任何一个空车位(只要我们走到了),也就是说,在之前的车位都不可行的前提下,我们接受每个车位的条件概率固定是 1−ρ ;而对于秘书问题,越往后我们遇到的总人数越多,当前的应试者是至今为止最优秀的那个的概率也就越小。在停车问题中,由于我们可以无限越过目标点去寻找车位,我们一个车位都找不到的概率为0;而在秘书问题中,应试者的数量是固定的,所以我们有一定的概率会招不到秘书(除非我们愿意将horizon无限拉长)。
书中没有给出最优阈值 n 的推导,在这里简单推一下。对细节不感兴趣的同学可以跳过这部分~
记 Si 为我们选择了编号 i 的车位, Bi 为编号 i 的车位是最优的事件。则有
P(Si)=ρn−i(1−ρ)
因为若我们选择停在车位 i ,那么车位 (i+1) 至 n 一定被占用了,且车位 i 一定没有被占用。
P(Bi|Si)={ρ2i−1(0
因为当 i>0 时,车位 i 最优当且仅当车位 (i−1) 至 −(i−1) 均被占用。当 −n≤i≤0 时,我们选到的车位 i 一定是最优的( Si 已经保证车位 (i−1) 至 −(i−1) 均被占用了)。当 i<−n 时,我们还需要车位 (n+1) 至 −i−1 被占用,才能确保车位 i 最优。
我们选择到最优车位的概率为
p=∑i=−∞nP(Si)P(Bi|Si)=∑i=1nρn−i(1−ρ)ρ2i−1+∑i=−n0ρn−i(1−ρ)+∑i=−∞−n−1ρn−i(1−ρ)ρ−n−1−i=ρn(1−ρn)+ρn(1−ρn+1)+ρ2n+11+ρ=[−(1+ρ)+ρ1+ρ]x2+2x
其中 x=ρn 。易知当 x=1+ρ1+ρ+ρ2 ,即 n=log(1+ρ)−log(1+ρ+ρ2)−logρ 时该概率取得最大值。当 ρ→1 时, ρn 约应取 23 。我们列出一些常用值,以及对比书中的结论:
占用概率rho(%) n (ours) n (in book) 0 0 0 50 0 1 75 1 3 80 1 4 85 2 5 90 3 7 95 7 14 96 9 17 97 13 23 98 20 35 99 40 69 99.9 405 693 我们的计算结果和书中有些出入,容易看出书中的数字是基于 ρn=12 得出的。作者可能使用了些许不同的假设来对问题建模。为了验证我们的结论,我们采用另外一种计算方式:
P(Bi)=ρ2|i|−1(1−ρ) ,因为车位 i 最优当且仅当编号绝对值小于 i 的车位均被占用。
P(Si|Bi)={0(n
因为当 i>n 时,我们的策略已经跳过车位 i 了,不可能选择到最优车位。当 0
容易验证 p=∑i=−∞nP(Bi)P(Si|Bi) 的结果与第一种方法一致。
停车问题有几个变型值得思考:
- 如果道路只是单侧无限长呢(即道路终止于目标点)?如果你在《教父1》的开头开车去婚礼派对,你就会遇到这个问题。(但大家都是去同一个目标点,我打赌他们用一个贪心的策略接龙停车就行了哈哈哈。)直觉是你应该更早地开始寻找车位。
- 如果允许在目标点处掉头呢?如果允许在任意点掉头呢?如果在道路是单侧无限长的条件下,这些变化又会意味着什么?
- 如果占用概率 ρ 并不是给定的,而要我们实时根据观察去估测呢?可以考虑预设一个 ρ 的prior,根据观察值去更新posterior(可以参见下一章的exploration vs. exploitation tradeoff)。如果 ρ 在空间上是变化的呢?是否能在 ρ 的梯度有某个界的条件下,给出最优策略?

柯里昂庄园外的停车问题。图源:《教父1》
急流勇退
有一句谚语叫"Quit when you're ahead",中文也有个词叫急流勇退。当我们已经取得一定收益,继续游戏便可能随时归零,什么才是最佳的收手时机?设想一个小偷,他每次行动都能获取一个固定的收益,却有90%的概率被抓到。被抓到则会失去所有已有的收益。那么他的最优策略是,行动的次数约等于每次行动能逃脱的概率除以被抓住的概率,也就是 90%/10%=9 次。
然而并不是所有问题都有一个最优的停止点。设想一个赌局,每次你都有一半的概率翻三倍,另一半的概率输光。按照最大化期望收益的目标,你应该不停地将游戏玩下去,而这恰恰确保了你迟早会输光。在这种情况下,我们或许应该引入一个效用函数来对递减的边际效用建模。我在下面的思考部分会提到。
我的一些思考
(1)最佳停止问题的假设说,我们预计观测的样本数 N 是固定的,然而最优策略却让我们实际上观测到的样本数少于预计值。这并不能使我们直观地感受到我们实际需要观测多少人。如果我们希望控制观测数量的数学期望 S ,而不是可能的最大观测数量 N 呢?(这样我们可以更好的预期观测的成本。)Look-and-Leap Rule策略让我们可以从给定的 N 计算出 S ,那么如果固定 S ,我们也可以反推 N ,从而得出look阶段的数量。然而有一个逻辑漏洞:我们的最佳策略是在假设最大观测数量为 N 的条件下得出的,并不意味着这也是观测数量的期望为 S 时的最佳策略。或许存在某种策略,它的最大观测数量不是固定值,或者根本没有上界,而相比于固定的最大观测数量,它更能帮我们找出群体中更加优秀的人?这个策略会是什么?
(2)在秘书问题中,我们的目标是最大化录取到最优秀应试者的概率。如果我们可以放松这个目标,也就是说,同时给录取到次优秀应试者一些奖励呢?如果运用最优策略,我们也有一定概率录取不到任何人,如何避免这种情况?我们或许可以给录取到每个名次的应试者的结果分配相应的效用(utility),然后最大化效用的期望。对于任意可能的、合理的效用函数,是否存在高效的算法确定它的最优策略?
(3)继续拓展效用函数的思路。如何确定效用函数的值?我们可能会设置一些效用等价条件,如:40%的概率录取到第一名和60%的概率录取到第三名,它的效用值等价于100%的概率录取到第二名,形式化地,
0.4U(1)+0.6U(3)=U(2)
那么,对于任何自洽的效用等价条件组,是否确定存在一个符合条件的效用函数?(感觉上是的)
最后分享书中一段很富有哲理的总结做结尾:
The secretary problem's most fundamental yet most unbelievable assumption -- its strict seriality, its inexorable one-way march -- is revealed to be the nature of time itself. As such, the explicit premise of the optimal stopping problem is the implicit premise of what it is to be alive. It's this that forces us to decide based on possibilities we've not yet seen, this that forces us to embrace high rates of failure even when acting optimally. No choice recurs. We may get similar choices again, but never the exact one. Hesitation -- inaction -- is just as irrevocable as action.
-
相关阅读:
Java项目:水果生鲜超市商城管理系统(java+SSM+JSP+jQuery+Mysql)
量子力学教程 第2.5章
Unity开发者必备的C#脚本技巧
ArcGis Pro Geometry 方法小记
操作系统【OS】调度算法对比图
动态爬虫管理平台构建与实现_kaic
LeetCode75——Day16
基于ssm的社区医院儿童预防接种管理系统设计与实现-计算机毕业设计源码+LW文档
git 进阶
Unity - ScriptableObject
- 原文地址:https://blog.csdn.net/wufaqidong1/article/details/126132968

