• [C++](19)AVL树插入，旋转，详细图解与代码

    文章目录

    概念

    在计算机科学中，AVL树（以发明者 Adelson-Velsky 和 Landis 命名）是一种自平衡的二叉搜索树（BST）。

    特点：

    1. 本身首先是一棵二叉搜索树。
    2. 带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。

    也就是说，AVL树，本质上是带了平衡功能的二叉搜索树。

    框架

    我们把它设计成三叉链表，即每个结点不仅可以找到它的左右孩子结点，也可以找到它的父亲结点。为了方便平衡，每个结点给一个平衡因子（balance factor）

    template<class K, class V>
struct AVLTreeNode
{
	pair<K, V> _kv;
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	// 右子树-左子树高度差
	int _bf;	// balance factor

	AVLTreeNode(const pair<K, V>& kv)
		: _kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _bf(0)
	{}
};

template<class K, class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:

private:
	Node* _root;
};

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28

    插入

    按搜索树规则插入

    bool Insert(const pair<K, V>& kv)
{
    if (_root == nullptr)
    {
        _root = new Node(kv);
        _root->_bf = 0;
        return true;
    }

    Node* parent = nullptr;
    Node* cur = _root;
    while (cur)
    {
        if (cur->_kv.first < kv.first)
        {
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_kv.first > kv.first)
        {
            parent = cur;
            cur = cur->_left;
        }
        else
        {
            return false;
        }
    }
    cur = new Node(kv);
    if (parent->_kv.first < kv.first)
        parent->_right = cur;
    else
        parent->_left = cur;
    cur->_parent = parent;
    
    //...
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37

    更新平衡因子

    首先要明确一点，一个结点的平衡因子由子树的高度差决定，也就是说，子树的高度变化只会影响祖先的平衡因子，对堂兄弟等结点没有影响。

    • 当你找到要插入的位置时，该位置的父结点平衡因子可能有三种情况：-1、0、1，这说明该结点一定只有 0 或 1 个孩子（因为至少留有一个要插入的位置），且高度为 1 或 2（叶子结点高度按 1 算）。

    • 若插入到左边，则父结点平衡因子 -1，插入到右边，父结点平衡因子 +1

    • 插入后，如果父结点的平衡因子变为 0，说明整棵树的高度没有改变，其上的各个祖先结点的平衡因子也就不需要更新

    • 插入后，如果父结点的平衡因子变为 -1 或 1，说明该子树的高度发生了改变，需要继续向上调整各个祖先结点的平衡因子。

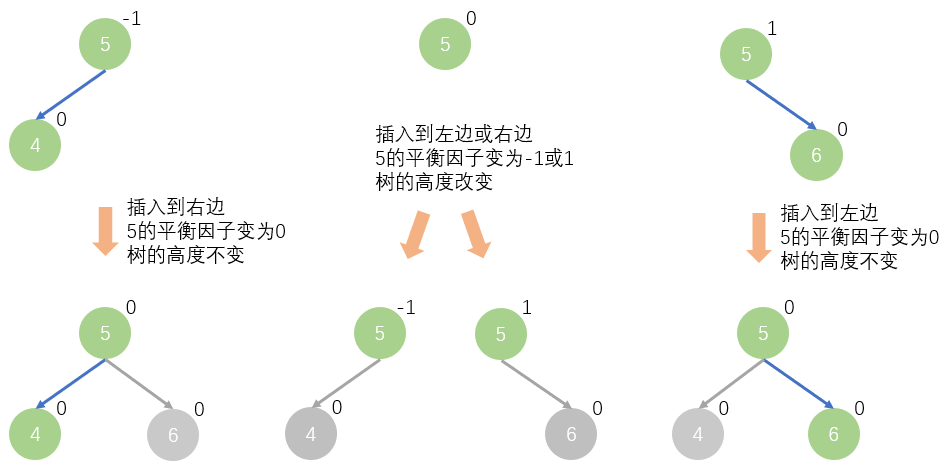
    更新平衡因子

    1. 更新后的平衡因子为-1、0、1都属于正常，不用调整，如果为-2、2，说明子树不平衡，需要调整，如果绝对值大于2，说明程序出错了，不满足AVL树的条件。
        //...

    // 更新平衡因子
    while (parent) // 最远更新到根
    {
        if (cur == parent->_right)
        {
            ++parent->_bf;
        }
        else
        {
            --parent->_bf;
        }
        // 是否继续更新
        if (parent->_bf == 0)// 为0，更新结束
        {
            break;
        }
        else if (parent->_bf == 1 || parent->_bf == -1)
        {
            cur = cur->_parent;
            parent = parent->_parent;
        }
        else if (parent->_bf == 2 || parent->_bf == -2)
        {
            // 子树不平衡，需要旋转处理

        }
        else
        {
            // 插入前就不满足AVL树的条件，程序出错
            assert(false);
        }
    }
    return true;
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36

    旋转

    对于不平衡的树，我们通过旋转来调整

    调整原则：

    • 保持搜索树的规则
    • 子树变平衡

    根据结点插入位置的不同，AVL树的旋转分为四种：

    1. 新结点插入在其较高右子树的右侧——右右：左旋

    下图是一个抽象图，绿三角表示任意的高度相等的AVL树

    具体旋转步骤为，将 subRL 变为 parent 的右子树，然后 parent 成为 subR 的左子树

    并且旋转完成后，整棵树的高度又回到插入元素之前，也就不需要继续向上调整平衡因子了。

    左旋

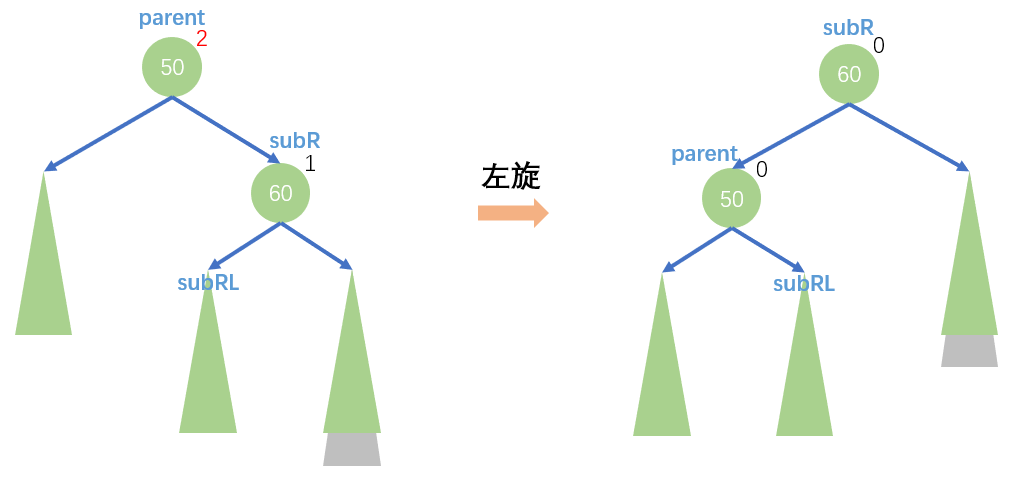
    写代码时要注意这是三叉链表，需要考虑结点的 _parent 指针。

    private:
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL) subRL->_parent = parent; // subRL有可能是空树，需要if判断

		Node* ppNode = parent->_parent; // 提前记录祖先，后面用来连接新的parent
		subR->_left = parent;
		parent->_parent = subR;

		if (parent == _root) // 如果parent就是根结点，那么新的根是subR
		{
			_root = subR;
			_root->_parent = nullptr;
		}
		else // 否则需要祖先来连接新的parent(即subR)，注意判断左右
		{
			if (parent == ppNode->_left)
			{
				ppNode->_left = subR;
			}
			else
			{
				ppNode->_right = subR;
			}
			subR->_parent = ppNode;
		}
        
		// 更新平衡因子
		parent->_bf = 0;
		subR->_bf = 0;
	}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    1. 新结点插入在其较高左子树的左侧——左左：右旋

    思路和左旋差不多：

    右旋

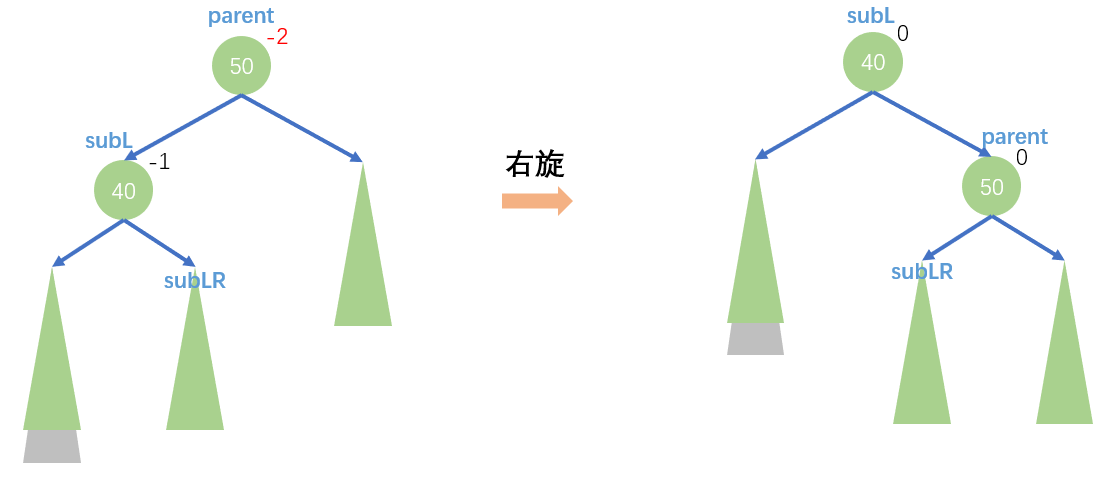
    	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR) subLR->_parent = parent;

		Node* ppNode = parent->_parent;
		subL->_right = parent;
		parent->_parent = subL;

		if (parent == _root)
		{
			_root = subL;
			_root->_parent = nullptr;
		}
		else
		{
			if (parent == ppNode->_left)
			{
				ppNode->_left = subL;
			}
			else
			{
				ppNode->_right = subL;
			}
			subL->_parent = ppNode;
		}
		parent->_bf = 0;
		subL->_bf = 0;
	}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    1. 新结点插入在较高左子树的右侧——左右：先左旋再右旋

    如下图，深绿色三角表示任意高度相等的AVL树，浅绿色三角比深绿色三角高度低1层

    这种情况下又分三个小情况

    1. 新结点插入在 subLR 的左子树，subLR 的平衡因子变为 -1
    2. 新结点插入在 subLR 的右子树，subLR 的平衡因子变为 1
    3. subLR 就是新结点，（即深绿色三角高度为 0，浅绿色三角不存在），subLR 的平衡因子为 0

    不管是哪种情况，旋转方式都一样，先对 subL 子树左旋，然后对 parent 右旋。

    旋转后的高度和插入前相等，也不用继续向上更新祖先的平衡因子。

    旋转后需要更新平衡因子，对应旋转前 subLR 的平衡因子，旋转后的平衡因子分别为：

    • 旋转前 sunLR：-1；旋转后 parent：1，subL：0，subLR：0
    • 旋转前 subLR：1；旋转后 parent：0，subL：-1，subLR：0
    • 旋转前 subLR：0；旋转后 parent：0，subL：0，subLR：0

    左右旋

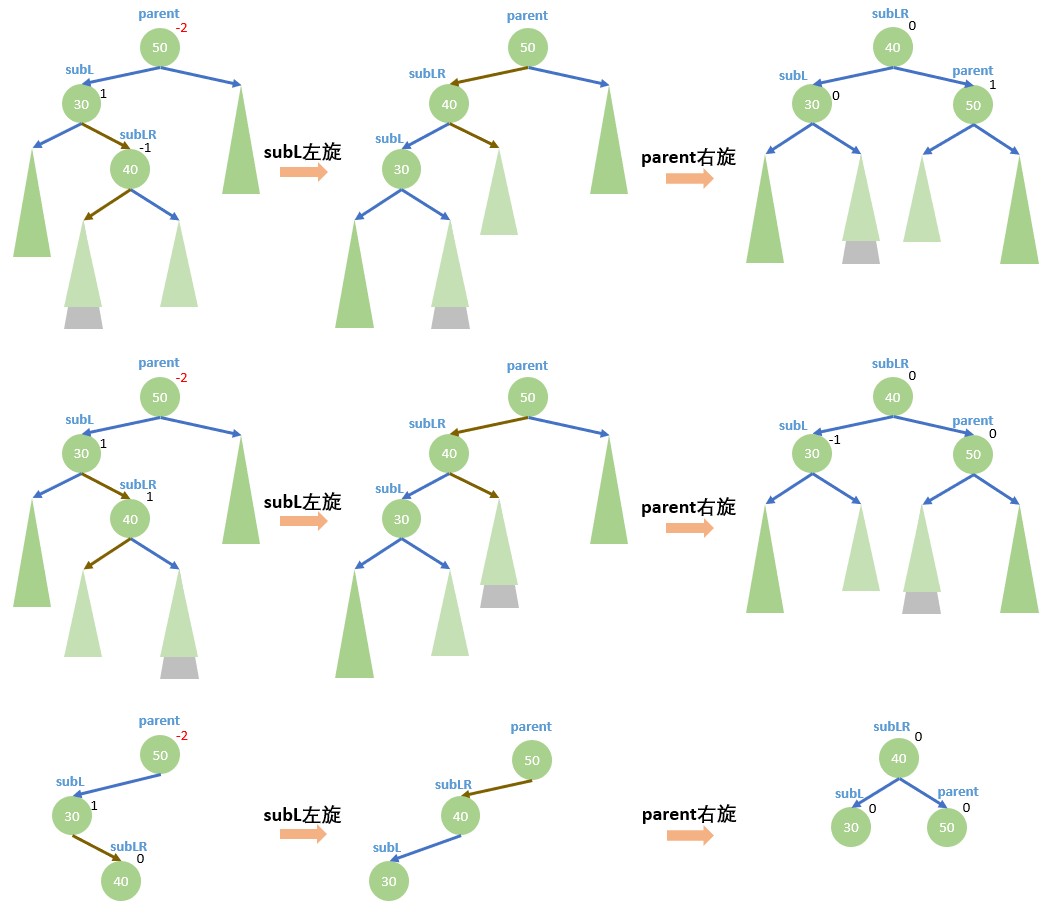
    代码其实很简单，因为可以复用已经写好的左旋和右旋。

    	void RotateLR(Node* parent)
	{
		Node* subL = parent->_left; // 提前记录subL和subLR以及subLR的bf，方便后面更新平衡因子
		Node* subLR = subL->_right;
		int bf = subLR->_bf;
		// 复用左旋和右旋
		RotateL(parent->_left); 
		RotateR(parent);
		// 更新平衡因子
		if (bf == 0)
		{
			parent->_bf = 0;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = 0;
			subL->_bf = -1;
			subLR->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 1;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    1. 新结点插入在较高右子树的左侧——右左：先右旋再左旋

    旋转后需要更新平衡因子，对应旋转前 subRL 的平衡因子，旋转后的平衡因子分别为：

    • 旋转前 sunRL：-1；旋转后 parent：0，subR：1，sunRL：0
    • 旋转前 sunRL：1；旋转后 parent：-1，subR：0，sunRL：0
    • 旋转前 sunRL：0；旋转后 parent：0，subR：0，sunRL：0

    右左旋

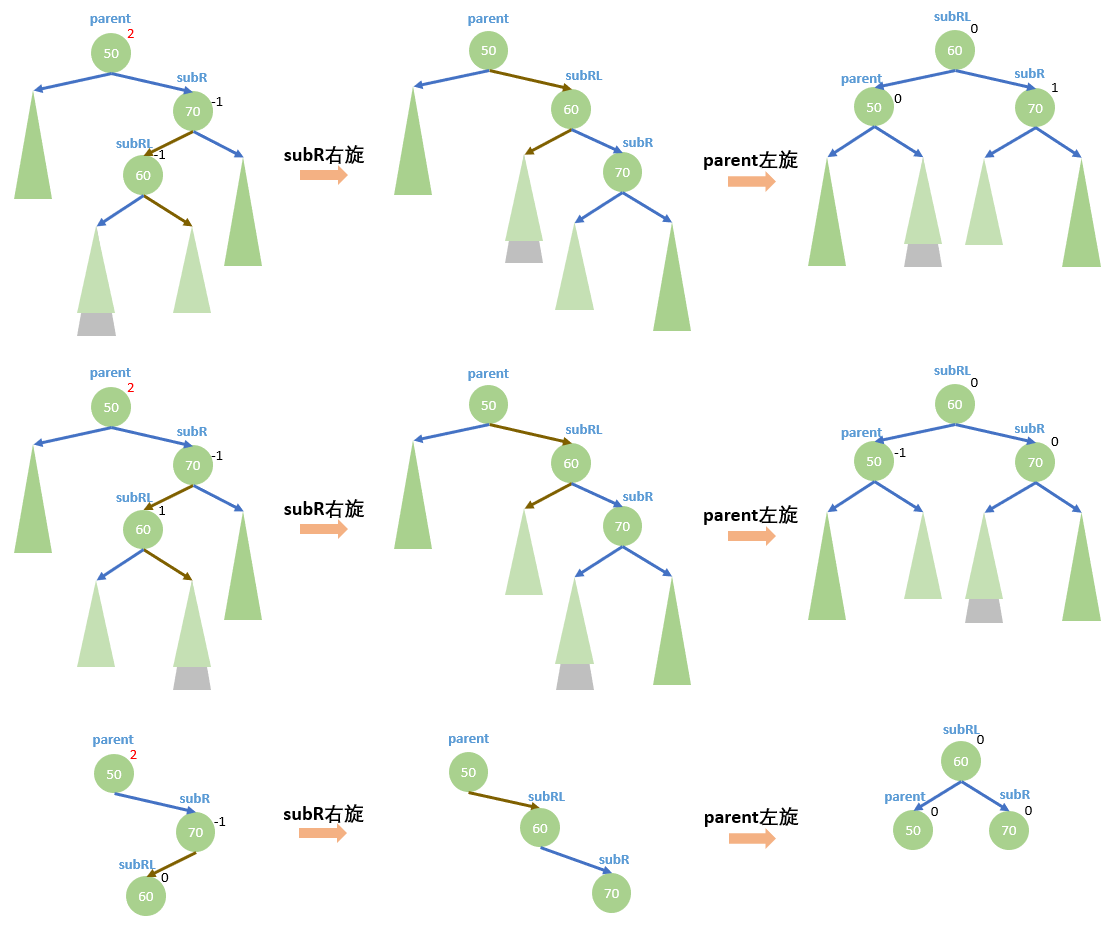
    	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right; // 提前记录subR和subRL以及subRL的bf，方便后面更新平衡因子
		Node* subRL = subR->_left;
		int bf = subRL->_bf;
		// 复用右旋和左旋
		RotateR(parent->_right);
		RotateL(parent);
		// 更新平衡因子
		if (bf == 0)
		{
			parent->_bf = 0;
			subR->_bf = 0;
			subRL->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = -1;
			subR->_bf = 0;
			subRL->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			subR->_bf = 1;
			subRL->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32

    到此为止，四种旋转调整的实现已经完成了，最后判断一下什么情况下用什么旋转：

    • parent的平衡因子为 2，cur的平衡因子为 1，右右，需要左旋
    • parent的平衡因子为 -2，cur的平衡因子为 -1，左左，需要右旋
    • parent的平衡因子为 -2，cur的平衡因子为 1，左右，需要左右双旋
    • parent的平衡因子为 2，cur的平衡因子为 -1，右左，需要右左双旋

    旋完直接 break 不用继续往上更新平衡因子。

    //...

else if (parent->_bf == 2 || parent->_bf == -2)
{
    // 子树不平衡，需要旋转处理
    if (parent->_bf == 2 && cur->_bf == 1) // 右右——左旋
    {
        RotateL(parent);
    }
    else if (parent->_bf == -2 && cur->_bf == -1) // 左左——右旋
    {
        RotateR(parent);
    }
    else if (parent->_bf == -2 && cur->_bf == 1) // 左右——左右旋
    {
        RotateLR(parent);
    }
    else if (parent->_bf == 2 && cur->_bf == -1) // 右左——右左旋
    {
        RotateRL(parent);
    }
    break;
}

//...

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25

    这里我们可以验证写出来的是不是AVL树，

    1. 通过层序遍历直观感受AVL树的长相。

    2. 通过逻辑检查是否符合AVL树的规则。

    public:
	void LevelOrder()
	{
		queue<Node*> que;
		if (_root != NULL) que.push(_root);
		while (!que.empty())
		{
			int size = que.size();
			for (int i = 0; i < size; i++)
			{
				Node* node = que.front();
				que.pop();
				cout << node->_kv.first << ' ';
				if (node->_left) que.push(node->_left);
				if (node->_right) que.push(node->_right);
			}
			cout << endl;
		}
	}

	bool IsAVLTree()
	{
		return _IsAVLTree(_root);
	}

private:
	bool _IsAVLTree(Node* root)
	{
		if (root == nullptr) return true; // 空树也是AVL树
		// 递归获得左右子树的高度
		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);
		int diff = rightHeight - leftHeight;
		if (abs(diff) > 1)	// 直接判断高度差是否符合要求
		{
			cout << root->_kv.first << "结点左右子树不平衡";
			return false;
		}
		if (diff != root->_bf) // 判断平衡因子是否符合实际
		{
			cout << root->_kv.first << "结点平衡因子不符合实际";
			return false;
		}

		return _IsAVLTree(root->_left) && _IsAVLTree(root->_right); // 递归检查各个结点
	}

	int _Height(Node* root)
	{
		if (root == nullptr) return 0;
		int leftDepth = _Height(root->_left);
		int rightDepth = _Height(root->_right);
		return  leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
	}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54

    插入随机值，然后检查：

    void test2()
{
	const size_t N = 100;
	vector<int> v;
	v.reserve(N);
	for (size_t i = 0; i < N; ++i)
	{
		v.push_back(rand());
	}

	AVLTree<int, int> t;
	for (auto e : v)
	{
		t.Insert(make_pair(e, 0));
	}
	t.LevelOrder();
	cout << endl;
	cout << t.IsAVLTree();
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19

    结果

    顺序插入检查：

    img

    结果完美符合预期！

    完整代码

    #pragma once
#include 
#include 
#include 
#include 
using namespace std;

template<class K, class V>
struct AVLTreeNode
{
	pair<K, V> _kv;
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	// 右子树-左子树高度差
	int _bf;	// balance factor

	AVLTreeNode(const pair<K, V>& kv)
		: _kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _bf(0)
	{}
};

template<class K, class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
	bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_bf = 0;
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(kv);
		if (parent->_kv.first < kv.first)
			parent->_right = cur;
		else
			parent->_left = cur;
		cur->_parent = parent;

		// 更新平衡因子
		while (parent) // 最远更新到根
		{
			if (cur == parent->_right)
			{
				++parent->_bf;
			}
			else
			{
				--parent->_bf;
			}
			// 是否继续更新
			if (parent->_bf == 0)// 为0，更新结束
			{
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1)
			{
				cur = cur->_parent;
				parent = parent->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				// 子树不平衡，需要旋转处理
				if (parent->_bf == 2 && cur->_bf == 1) // 右右——左旋
				{
					RotateL(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == -1) // 左左——右旋
				{
					RotateR(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == 1) // 左右——左右旋
				{
					RotateLR(parent);
				}
				else if (parent->_bf == 2 && cur->_bf == -1) // 右左——右左旋
				{
					RotateRL(parent);
				}
				break;
			}
			else
			{
				// 插入前就不满足AVL树的条件，程序出错
				assert(false);
			}
		}
		return true;
	}

	void LevelOrder()
	{
		queue<Node*> que;
		if (_root != NULL) que.push(_root);
		while (!que.empty())
		{
			int size = que.size();
			for (int i = 0; i < size; i++)
			{
				Node* node = que.front();
				que.pop();
				cout << node->_kv.first << ' ';
				if (node->_left) que.push(node->_left);
				if (node->_right) que.push(node->_right);
			}
			cout << endl;
		}
	}

	bool IsAVLTree()
	{
		return _IsAVLTree(_root);
	}

private:
	bool _IsAVLTree(Node* root)
	{
		if (root == nullptr) return true;

		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);
		int diff = rightHeight - leftHeight;
		if (abs(diff) > 1)
		{
			cout << root->_kv.first << "结点左右子树不平衡";
			return false;
		}
		if (diff != root->_bf)
		{
			cout << root->_kv.first << "结点平衡因子不符合实际";
			return false;
		}

		return _IsAVLTree(root->_left) && _IsAVLTree(root->_right);
	}

	int _Height(Node* root)
	{
		if (root == nullptr) return 0;
		int leftDepth = _Height(root->_left);
		int rightDepth = _Height(root->_right);
		return  leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
	}

private:
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL) subRL->_parent = parent; // subRL有可能是空树，需要if判断

		Node* ppNode = parent->_parent; // 提前记录祖先，后面用来连接新的parent
		subR->_left = parent;
		parent->_parent = subR;

		if (parent == _root) // 如果parent就是根结点，那么新的根是subR
		{
			_root = subR;
			_root->_parent = nullptr;
		}
		else // 否则需要祖先来连接新的parent(即subR)，注意判断左右
		{
			if (parent == ppNode->_left)
			{
				ppNode->_left = subR;
			}
			else
			{
				ppNode->_right = subR;
			}
			subR->_parent = ppNode;
		}

		// 更新平衡因子
		parent->_bf = 0;
		subR->_bf = 0;
	}

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR) subLR->_parent = parent;

		Node* ppNode = parent->_parent;
		subL->_right = parent;
		parent->_parent = subL;

		if (parent == _root)
		{
			_root = subL;
			_root->_parent = nullptr;
		}
		else
		{
			if (parent == ppNode->_left)
			{
				ppNode->_left = subL;
			}
			else
			{
				ppNode->_right = subL;
			}
			subL->_parent = ppNode;
		}
		parent->_bf = 0;
		subL->_bf = 0;
	}

	void RotateLR(Node* parent)
	{
		Node* subL = parent->_left; // 提前记录subL和subLR以及subLR的bf，方便后面更新平衡因子
		Node* subLR = subL->_right;
		int bf = subLR->_bf;
		// 复用左旋和右旋
		RotateL(parent->_left); 
		RotateR(parent);
		// 更新平衡因子
		if (bf == 0)
		{
			parent->_bf = 0;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = 0;
			subL->_bf = -1;
			subLR->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 1;
			subL->_bf = 0;
			subLR->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right; // 提前记录subR和subRL以及subRL的bf，方便后面更新平衡因子
		Node* subRL = subR->_left;
		int bf = subRL->_bf;
		// 复用右旋和左旋
		RotateR(parent->_right);
		RotateL(parent);
		// 更新平衡因子
		if (bf == 0)
		{
			parent->_bf = 0;
			subR->_bf = 0;
			subRL->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = -1;
			subR->_bf = 0;
			subRL->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			subR->_bf = 1;
			subRL->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}
private:
	Node* _root = nullptr;
};

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 39
    • 40
    • 41
    • 42
    • 43
    • 44
    • 45
    • 46
    • 47
    • 48
    • 49
    • 50
    • 51
    • 52
    • 53
    • 54
    • 55
    • 56
    • 57
    • 58
    • 59
    • 60
    • 61
    • 62
    • 63
    • 64
    • 65
    • 66
    • 67
    • 68
    • 69
    • 70
    • 71
    • 72
    • 73
    • 74
    • 75
    • 76
    • 77
    • 78
    • 79
    • 80
    • 81
    • 82
    • 83
    • 84
    • 85
    • 86
    • 87
    • 88
    • 89
    • 90
    • 91
    • 92
    • 93
    • 94
    • 95
    • 96
    • 97
    • 98
    • 99
    • 100
    • 101
    • 102
    • 103
    • 104
    • 105
    • 106
    • 107
    • 108
    • 109
    • 110
    • 111
    • 112
    • 113
    • 114
    • 115
    • 116
    • 117
    • 118
    • 119
    • 120
    • 121
    • 122
    • 123
    • 124
    • 125
    • 126
    • 127
    • 128
    • 129
    • 130
    • 131
    • 132
    • 133
    • 134
    • 135
    • 136
    • 137
    • 138
    • 139
    • 140
    • 141
    • 142
    • 143
    • 144
    • 145
    • 146
    • 147
    • 148
    • 149
    • 150
    • 151
    • 152
    • 153
    • 154
    • 155
    • 156
    • 157
    • 158
    • 159
    • 160
    • 161
    • 162
    • 163
    • 164
    • 165
    • 166
    • 167
    • 168
    • 169
    • 170
    • 171
    • 172
    • 173
    • 174
    • 175
    • 176
    • 177
    • 178
    • 179
    • 180
    • 181
    • 182
    • 183
    • 184
    • 185
    • 186
    • 187
    • 188
    • 189
    • 190
    • 191
    • 192
    • 193
    • 194
    • 195
    • 196
    • 197
    • 198
    • 199
    • 200
    • 201
    • 202
    • 203
    • 204
    • 205
    • 206
    • 207
    • 208
    • 209
    • 210
    • 211
    • 212
    • 213
    • 214
    • 215
    • 216
    • 217
    • 218
    • 219
    • 220
    • 221
    • 222
    • 223
    • 224
    • 225
    • 226
    • 227
    • 228
    • 229
    • 230
    • 231
    • 232
    • 233
    • 234
    • 235
    • 236
    • 237
    • 238
    • 239
    • 240
    • 241
    • 242
    • 243
    • 244
    • 245
    • 246
    • 247
    • 248
    • 249
    • 250
    • 251
    • 252
    • 253
    • 254
    • 255
    • 256
    • 257
    • 258
    • 259
    • 260
    • 261
    • 262
    • 263
    • 264
    • 265
    • 266
    • 267
    • 268
    • 269
    • 270
    • 271
    • 272
    • 273
    • 274
    • 275
    • 276
    • 277
    • 278
    • 279
    • 280
    • 281
    • 282
    • 283
    • 284
    • 285
    • 286
    • 287
    • 288
    • 289
    • 290
    • 291
    • 292
    • 293
    • 294
    • 295
    • 296
    • 297
    • 298
    • 299
    • 300
    • 301
    • 302
    • 303
    • 304
    • 305
    • 306
    • 307
    • 308
  • 相关阅读:
    详解和实现数据表格中的行数据合并功能
    利用大数据和API优化电商决策：商品性能分析实践
    IPV6协议总结
    面向6G网络的水下光通信系统
    非自交任意多边形与矩形框的交集面积计算方法
    大数据分析实践 | 过滤和抽样
    嵌入式学习 基础概念合集
    jar增量打包
    A fuzzy spectral clustering algorithm for hyperspectral image
    YOLOv5-PTQ量化部署
  • 原文地址：https://blog.csdn.net/CegghnnoR/article/details/126131403