活动地址：CSDN21天学习挑战赛

1 简介

        逻辑回归不是用于回归任务而是分类任务

2 逻辑回归

2.1 逻辑斯蒂分布

        设X是连续随机变量，X服从Logistic distribution。

分布函数为：

图像为：

 

2.2 二项逻辑回归模型

        二项逻辑回归模型是用条件概率表达的一种分类模型，随机变量X为实数，随机变量Y的取值为1,0.

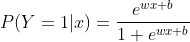
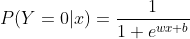
可以将偏置b省略来简化模型。

2.3 模型参数估计

        可以利用极大似然估计法来估计模型的参数w,求似然函数L(w)的最大值L得到w的估计值。

若w的极大似然估计值为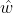，则所得到的Logistic模型为：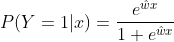

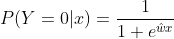
现在目标函数为似然函数，对目标函数的优化方式有梯度下降法和拟牛顿法。

3 最大熵模型

        逻辑斯谛回归模型与最大熵模型都属于对数线性模型。优化模型时，一般选择熵最大的模型。最大熵模型是在满足约束条件的模型中选择上最熵最大的模型。

用期望来表示约束条件：

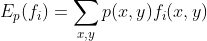
实验部分：

class LogisticReressionClassifier:
    def __init__(self, max_iter=200, learning_rate=0.01):
        self.max_iter = max_iter
        self.learning_rate = learning_rate
 
    def sigmoid(self, x):
        return 1 / (1 + exp(-x))
 
    def data_matrix(self, X):
        data_mat = []
        for d in X:
            data_mat.append([1.0, *d])
        return data_mat
 
    def fit(self, X, y):
        data_mat = self.data_matrix(X)  # m*n
        self.weights = np.zeros((len(data_mat[0]), 1), dtype=np.float32)
 
        for iter_ in range(self.max_iter):
            for i in range(len(X)):
                result = self.sigmoid(np.dot(data_mat[i], self.weights))
                error = y[i] - result
                self.weights += self.learning_rate * error * np.transpose(
                    [data_mat[i]])
        print('LogisticRegression Model(learning_rate={},max_iter={})'.format(
            self.learning_rate, self.max_iter))
 
    #     return -(self.weights[0] + self.weights[1] * x) / self.weights[2]
 
    def score(self, X_test, y_test):
        right = 0
        X_test = self.data_matrix(X_test)
        for x, y in zip(X_test, y_test):
            result = np.dot(x, self.weights)
            if (result > 0 and y == 1) or (result < 0 and y == 0):
                right += 1
        return right / len(X_test)

参考

《统计学习方法》——李航