牛客2022 暑期多校3 H Hacker（SAM + 线段树查询区间内部最大子段和）

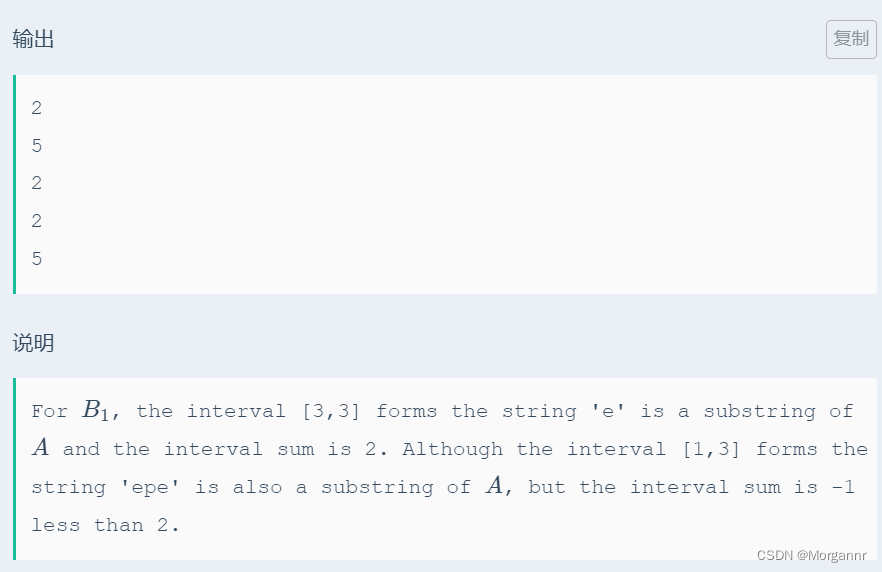
题意：

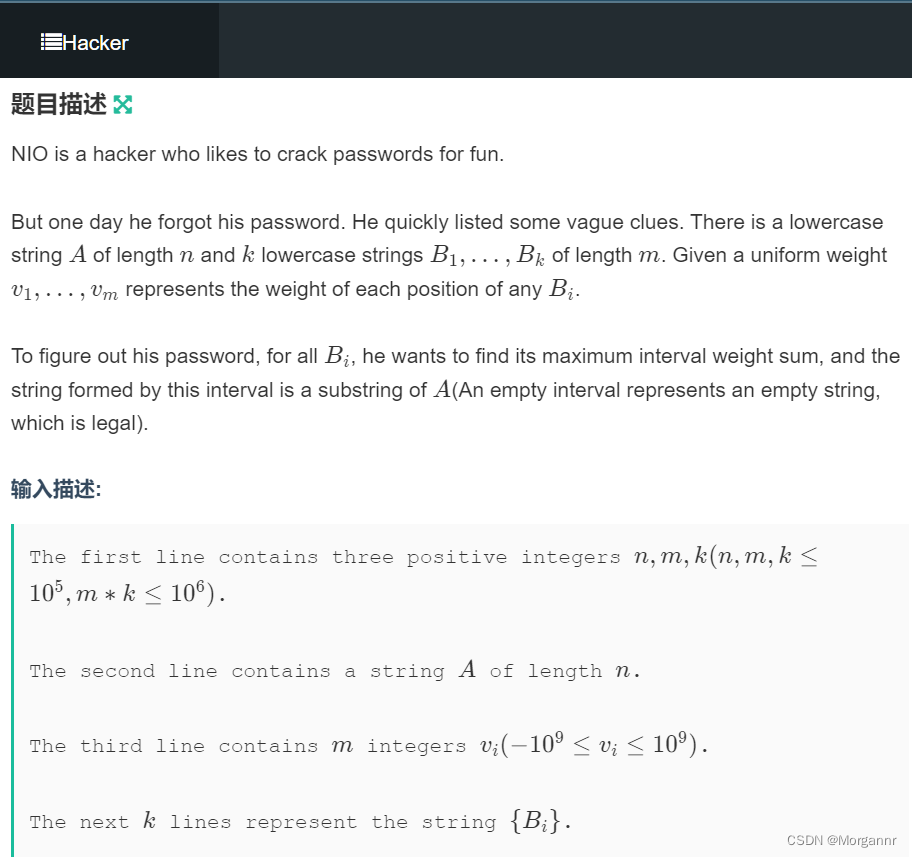
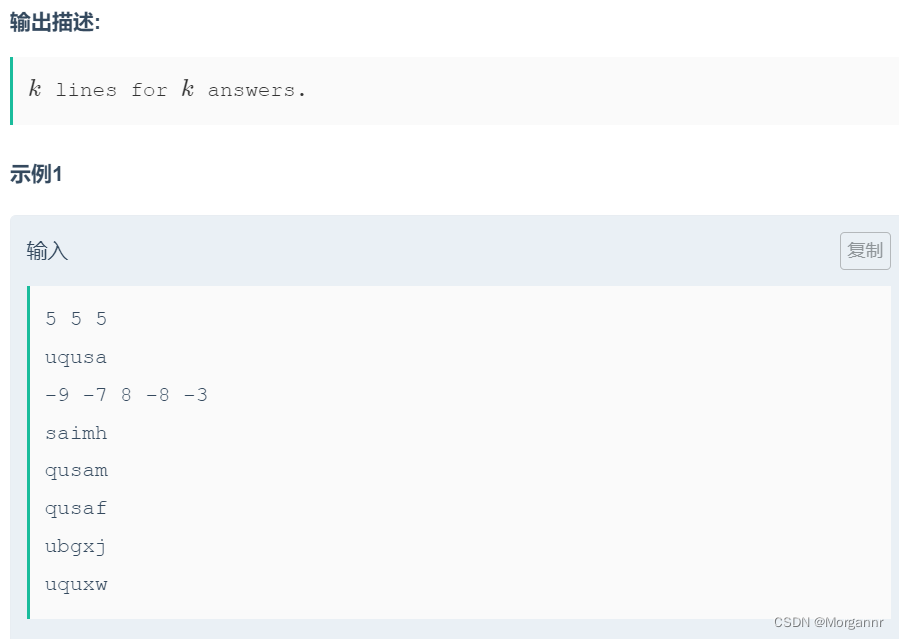
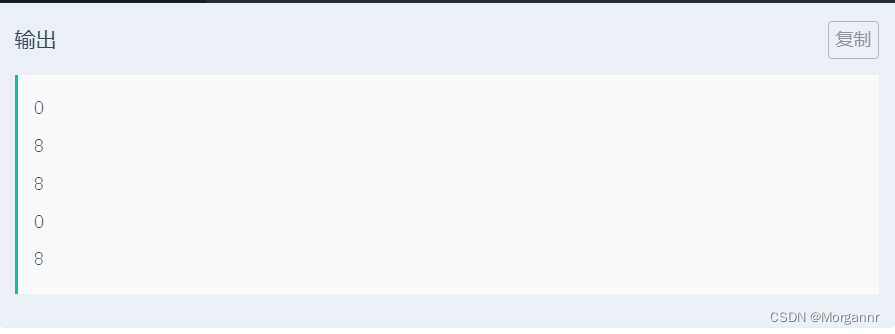
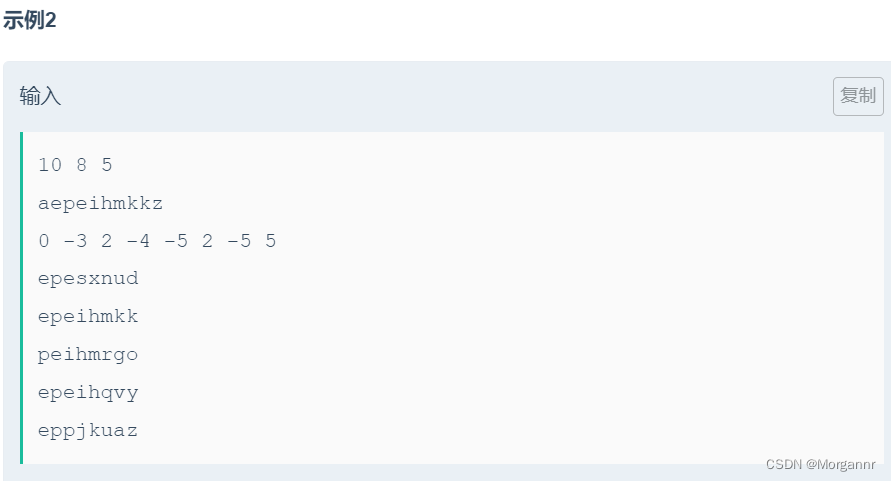
给定 主串 以及 若干副串，副串长度固定，每个位置 都有一个 权值，要求在 主串和副串的公共子串中 找到一个 连续区间，使得 连续区间的权值和最大，求 最大权值和。

思路：

本题其实就是 这两道板子题：SPOJ 2774 Longest Common Substring 和 AcWing 245. 你能回答这些问题吗 硬生生的结合版，

用 SAM 维护 主串 和 枚举的各个副串 的 所有公共子串，对于 主串 与 某个副串 的 某个公共子串所在区间，我们利用 线段树 维护 区间内部最大子段和 即可。

简单题，但是比赛的时候由于没学 SAM 而寄了

不过值得一提的是，代码中的将 主串 和 副串 的 所有公共子串所在区间 提取出来的操作：

int p = 1, t = 0;
for (int j = 1; ss[j]; ++j) {
	int sta, ed;	//存储每个公共子串所在的合法区间左右端点
	int c = ss[j] - 'a';
	while (p > 1 && !ch[p][c]) {	//经典匹配操作
		p = fa[p];
		t = len[p];
	}
	ed = j - 1;	//此时由于当前字符s[j]还未匹配，因此右端点为j-1
	if (ch[p][c]) {	//如果当前字符s[j]匹配成功，则右端点移至j，且LCS的长度t++
		p = ch[p][c];
		++t;
		++ed;
	}
	if (t) {	//当前公共子串长度不为0，即合法，根据其长度t计算左端点sta（因为右端点ed已经求出，相减即可）
		sta = ed - t + 1;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

时间复杂度：

$O(nlogn)$

代码：

#include <bits/stdc++.h>

using namespace std;
//#define map unordered_map
#define int long long
int n, m, k;
const int N = 1e5 + 10, M = N << 1;
int fa[M], ch[M][26], len[M], cnt[M];
int np = 1, tot = 1;
char s[N], ss[N];
int w[N];
struct node {
	int l, r;
	int tmax, sum, lmax, rmax;
} t[N << 2];

void pushup(node& u, node& l, node& r) {
	u.sum = l.sum + r.sum;
	u.tmax = max(max(l.tmax, r.tmax), l.rmax + r.lmax);
	u.lmax = max(l.lmax, l.sum + r.lmax);
	u.rmax = max(r.rmax, r.sum + l.rmax);
}

void pushup(int u) {
	pushup(t[u], t[u << 1], t[u << 1 | 1]);
}

void build(int u, int l, int r) {
	t[u] = { l, r };
	if (l == r) {
		t[u].tmax = t[u].sum = t[u].lmax = t[u].rmax = w[l];
		return;
	}

	int mid = l + r >> 1;
	build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
	pushup(u);
}

node ask(int u, int l, int r) {
	if (l <= t[u].l && r >= t[u].r) return t[u];

	int mid = t[u].l + t[u].r >> 1;
	if (r <= mid) return ask(u << 1, l, r);
	else if (l >= mid + 1) return ask(u << 1 | 1, l, r);
	else {
		auto left = ask(u << 1, l, r);
		auto right = ask(u << 1 | 1, l, r);
		node res;
		pushup(res, left, right);
		return res;
	}
}

void extend(int c) {
	int p = np;
	np = ++tot;
	len[np] = len[p] + 1, cnt[np] = 1;
	while (p && !ch[p][c]) {
		ch[p][c] = np;
		p = fa[p];
	}
	if (!p) {
		fa[np] = 1;
	}
	else {
		int q = ch[p][c];
		if (len[q] == len[p] + 1) {
			fa[np] = q;
		}
		else {
			int nq = ++tot;
			len[nq] = len[p] + 1;
			fa[nq] = fa[q], fa[q] = fa[np] = nq;
			while (p && ch[p][c] == q) {
				ch[p][c] = nq;
				p = fa[p];
			}
			memcpy(ch[nq], ch[q], sizeof ch[q]);
		}
	}
}

signed main()
{
	cin >> n >> m >> k;
	cin >> s + 1;
	for (int i = 1; i <= n; ++i) {
		extend(s[i] - 'a');
	}
	for (int i = 1; i <= m; ++i) {
		scanf("%lld", &w[i]);
	}
	build(1, 1, m);
	for (int i = 0; i < k; ++i) {
		scanf("%s", ss + 1);
		int p = 1, t = 0;
		int res = -2e18;
		for (int j = 1; ss[j]; ++j) {
			int sta, ed;
			int c = ss[j] - 'a';
			while (p > 1 && !ch[p][c]) {
				p = fa[p];
				t = len[p];
			}
			ed = j - 1;
			if (ch[p][c]) {
				p = ch[p][c];
				++t;
				++ed;
			}
			if (t) {
				sta = ed - t + 1;
				res = max(max(res, ask(1, sta, ed).tmax), (int)0);
			}
		}
		printf("%lld\n", res);
	}

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121